In the given figure, two chordsAB and CD of a circle AYDZBWCX intersect at right angles. Prove that
arc CXA + arc DZB = arc AYD + arc BWC = semicircle.

GIVEN Two chords AB and CD of a circle AYDZBWCX, intersecting at a point such that AB⊥CD.
CONSTRUCTION Let O be the centre of the given circle. Join OA, OB,OC,OD and BC.
PROOF In ΔEBC, we have
∠EBC+∠ECB+∠CEB=180∘
⇒∠EBC+∠ECB=180∘−∠CEB=(180∘−90∘)=90∘
⇒∠ABC+∠DCB=90∘ .....(i)
Since the angle subtended by an arc of a circle at its centre is double the angle subtended by it any point of the remaining part of the circle, we have
∠AOC=2∠ABC and ∠DOB=2∠DCB
⇒∠AOC+∠DOB=2(∠ABC+∠DCB)=(2×90∘)=180∘ [ using (i) ]
⇒ arc CXA + arc DZB = semicircle.
Semilarly, arc AYD + arc BWC = semicircle.
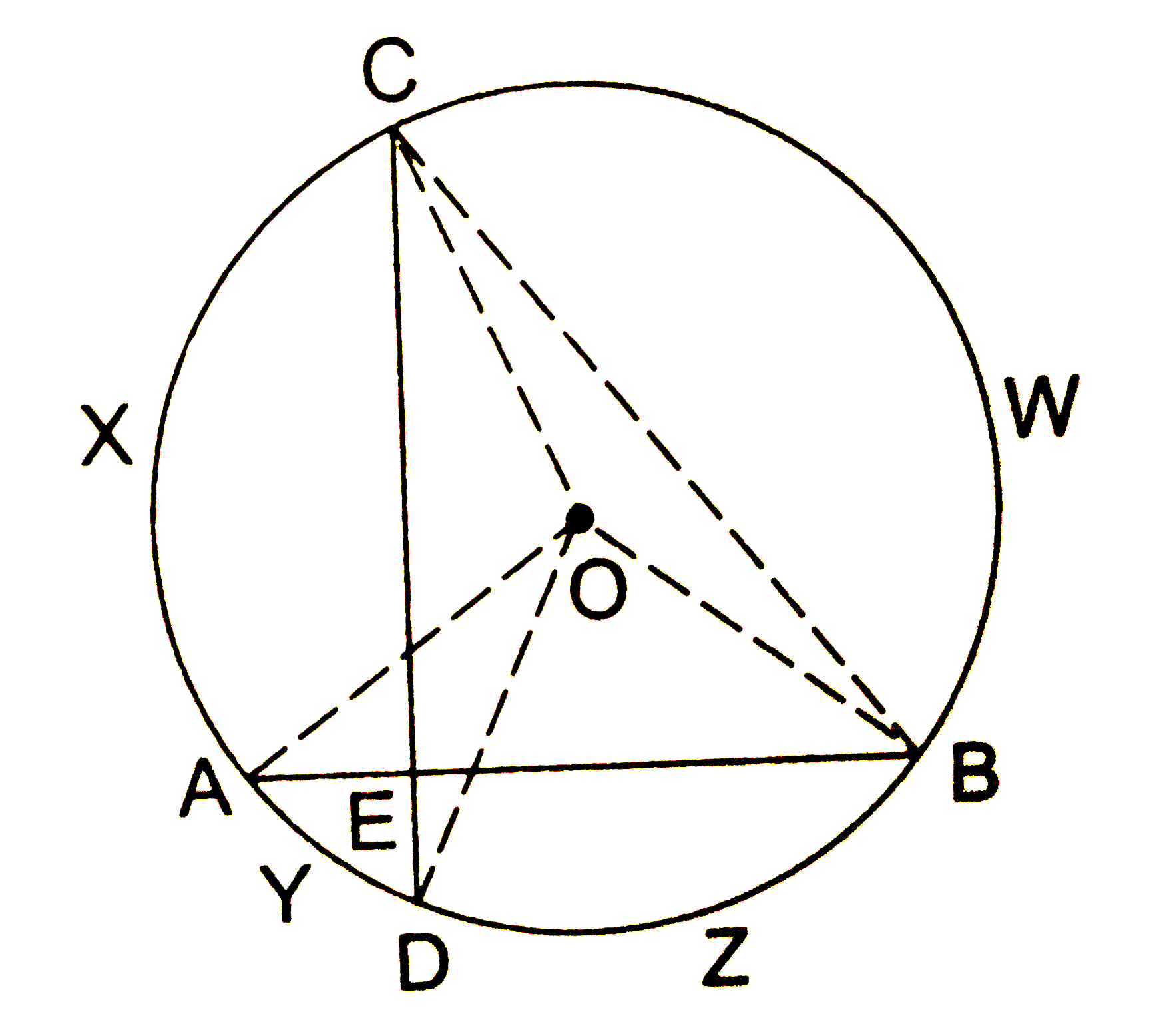
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
If two chords AB and CD of a circle AYDZBWCX intersect at right angles, then prove that arc CXA+arc DZB=arc AYD+arc BWC =semi-circle.

View SolutionIn the given figure, name the following:

an arc
View SolutionIf the perpendicular bisector of a chord AB of a circle PXAQBY intersects the circle at P and Q, prove that arc PXA≅arc PYB.

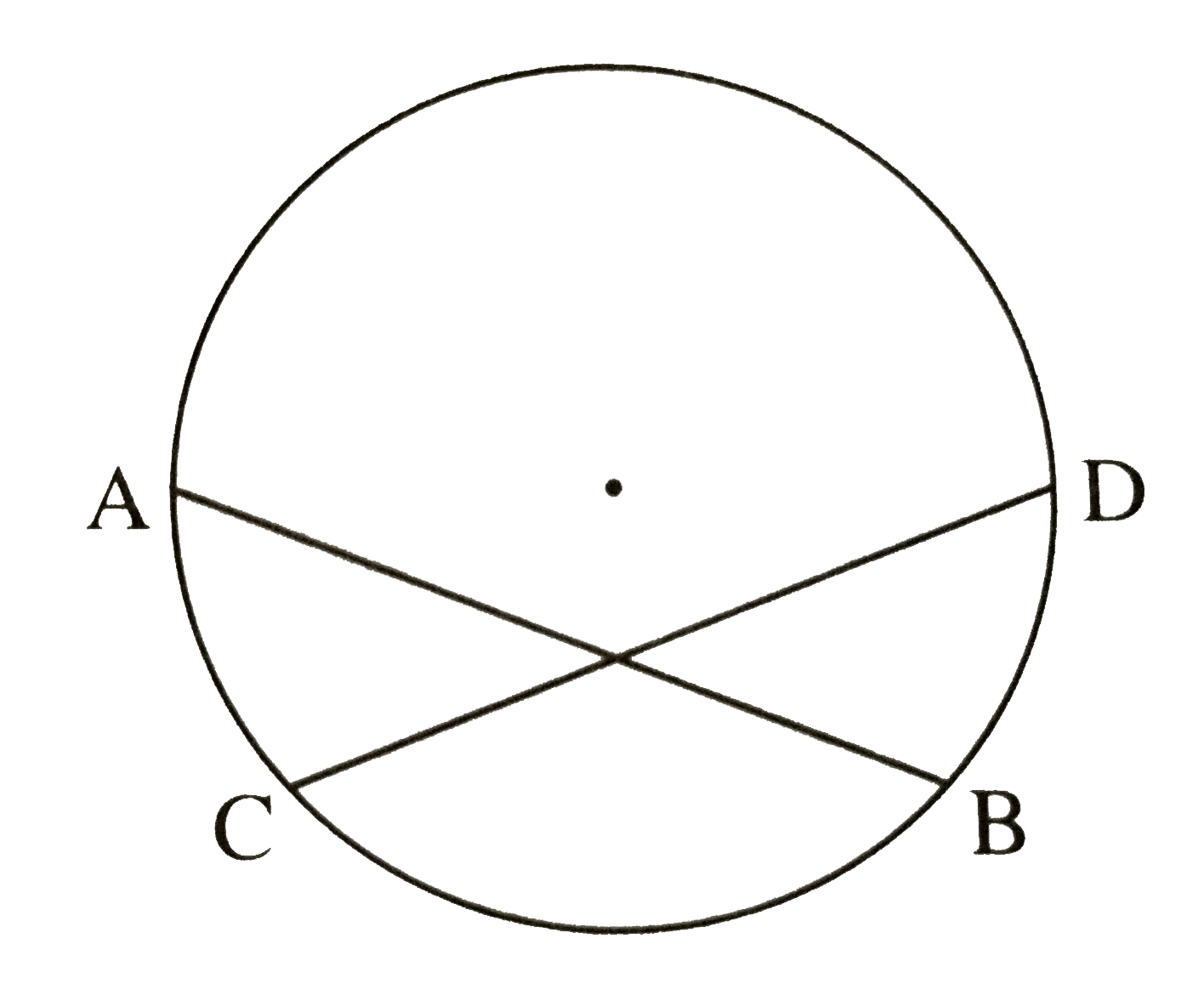
View SolutionIn figure, chord AB ≅ chord CD, Prove that, arc AC ≅ arc BD.
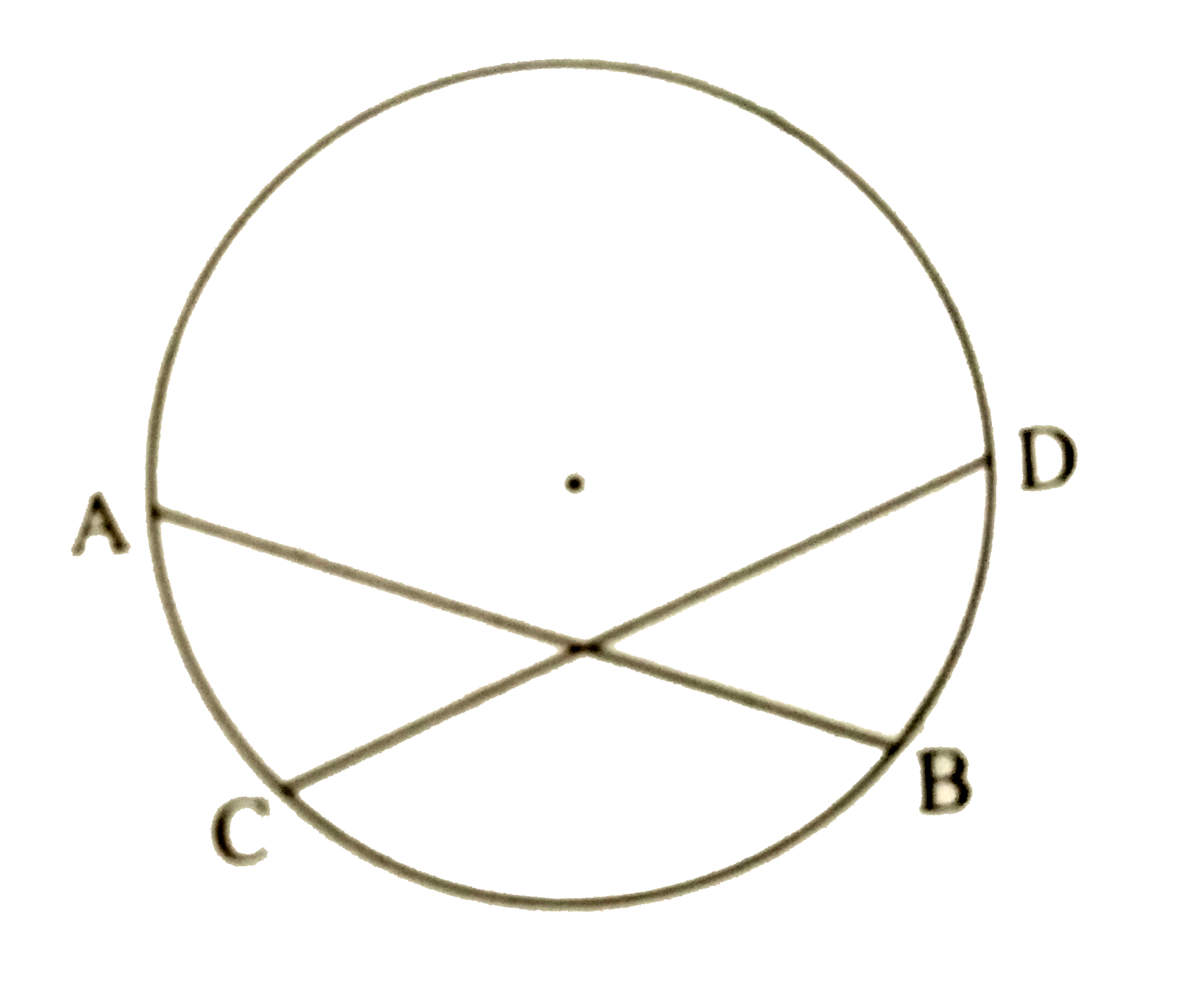
View SolutionIn the figure, chord AB ≅ chord CD
Prove that ,
ar AC ≅ arc BD
View SolutionIn the given figure, name the following:
two minor and major arcs
View SolutionIn the given figure , O is the centre of the circle. If m(arc AXB)=80∘, then m∠AOB=

View SolutionChords AB and CD of a circle intersect in point Q in interior of a circle. If m(arc AD)=25∘ and m(arc BC)=31∘, find ∠BQC.

View SolutionIn the figure, AB and CD are two chords of a circle, interacting each other at a point E. Prove that ∠AEC = 1/2(angle subtended by arc CXA. at the centre + angle subtended by arc DYB at the centre).
View SolutionIn figure, △QRS is an equilateral triangles. Prove that,
(1) arcRS≅arcQS≅arcQR
(2) m(arcQRS)=240∘.

View Solution
