Obtain the formula for the electric field due to a long thin wire of uniform linear charge density E without using Gauss's law. (Hint: Use Coulomb's law directly and evaluate the necessary integral.)

Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

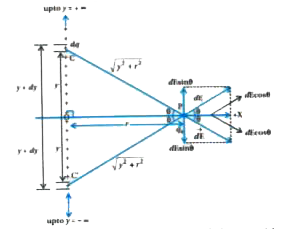
Consider infinitely extended line of charge with constant linear charge density $λ$ . Let us determine its electric field at perpendicular distance r say at point P as shown in the figure. For this consider a charge element dq at distance y from central point O. Here, $d q = λ d y$
$(∴ λ = \frac{d q}{d y})$
Magnitude of Coulombian force exerted by above charge element dq on test charge $q_{0}$ placed at point P is,
$d F = k \frac{(d q) q_{0}}{{(C P)}^{2}} = \frac{k (d q) q_{0}}{y^{2} + r^{2}}$ ........(1)
Magnitude of electric field of charge element dq at point P is,
$d E = \frac{d F}{q_{0}} = \frac{k d q}{y^{2} + r^{2}}$ .........(2)
Similary magnitude of electric field of charge element dq (selected on opposite side of central point O) at point P is also, $d E = \frac{k d q}{y^{2} + r^{2}}$
When we resolve above two electric fields into two mutually perpendicular components at point p we find that dEsinG components cancel each other (because of equal magnitudes and opposite directions). Hence, we get electric field at point P only due to $d E \cos θ$ components which are in same directions and so we can make their scalar addition to find resultant electric field E at point P Thus,
$E = \int d E \cos θ$
$\int \frac{k d q}{y^{2} + r^{2}} . \frac{r}{\sqrt{y^{2} + r^{2}}}$
From eqn. (2) and from $Δ C O P$
$∴ E = \int k λ d y \times \frac{r}{{(y^{2} + r^{2})}^{3 / 2}}$ ...........(3)
In right angled $△ C O P$
$\tan θ = \frac{y}{r} \Rightarrow y = r \tan θ$ .......(4)
For a given point P value of r is constant and so from above equation,
$\frac{d y}{d θ} = r \frac{d}{d θ} (\tan θ)$
$∴ \frac{d y}{d θ} = r \sec^{2} θ$
$∴ d y = r \sec^{2} θ d θ$ ........(5)
Now, ${(y^{2} + r^{2})}^{3 / 2} = {(r^{2} \tan^{2} θ + r^{2})}^{3 / 2}$ (From equation (4))
$= {(r^{2} \sec^{2} θ)}^{3 / 2}$
$= r^{2} \sec^{3} θ$ .........(6)
From equation (4)
$\tan θ = \frac{y}{r}$
When $y = - \infty, \tan θ = - \infty \Rightarrow θ = - \frac{π}{2}$
$y = + \infty, \tan θ = + \infty \Rightarrow θ = + \frac{π}{2}$ ............(7)
From eqn (3), (5),(6) and (7),
$E = \int_{- π / 2}^{+ π / 2} k λ (r \sec^{2} θ d θ) \times \frac{r}{r^{3} \sec^{3} θ}$
$∴ E = \frac{k λ}{r} {\sin (\frac{π}{2}) - \sin (- \frac{π}{2})}$
$∴ E = \frac{2 k λ}{r}$
$∴ E = \frac{λ}{2 π ε_{0} r} (∴ k = \frac{1}{4 π ε_{0}})$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-ELECTRIC CHARGES AND FIELDS -SECTION B NUMERICALS (ADDITONAL EXERCISE)

Home
Ask Doubt
Profile