A hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hold is $\frac{σ}{2 π ε_{0}} ˆ n$ where $ˆ n$ is the unit vector in the outward normal direction, and a is the surface charge density near the hole.
Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

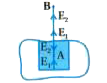
As shown in figure, assume that the hole on the conducting surface is filled by conductor. According to Gauss.s law, at A on surface,
$\oint \to E . d \to S = \frac{q}{ε_{0}}$
$E d S {cos 0}^{\circ} = \frac{σ d S}{ε_{0}} [∴ σ = \frac{q}{d s}]$
$∴ E . d S = \frac{σ d S}{ε_{0}}$
$∴ \to E = \frac{σ}{ε_{0}} . ˆ n$
Which is electric field outside the conductor. Above electric field can be written as,
$\to E = {\to E}_{1} + {\to E}_{2}$ ..........(2)
where ${\to E}_{1}$ = electric field at point $P_{0}$ just outside the conductor (adjacent to point P on the surface) due to charge at point P and ${\to E}_{2}$ = electric field at point P (or at $P_{0}$ ) flue to remaining charges on the given charged hollow conductor.
When hollow charged conductor does not have any hole at point P on the surface we have ${\to E}_{1}$ and $E_{2}$ pointing along $ˆ n$ and so from equation (2), we can write,
$E = E_{1} + E_{2} = \frac{σ}{ε_{0}}$ ...........(3)
Now consider point $P_{p}$ , adjacent to point P and just inside the conductor in figure (a), where resultant electric field $\to E$ is $\to 0$ . Hence,
$\to E = {\to E}_{1} + {\to E}_{2} = \to 0$
$∴ {\to E}_{1} = - {\to E}_{2}$
$∴ {\to E}_{1} = E_{2}$ (Taking magnitude).......(4)
From eqn. (3) and (4)
$2 E_{2} = \frac{σ}{ε_{0}}$
$∴ E_{2} = \frac{σ}{2 ε_{0}}$ ..........(5)
Now, when we have a hole at point P electric field at point P,- in the hole due to remaining charges will be,
$E_{2} = \frac{σ}{2 ε_{0}} ˆ n$ .............(6)

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-ELECTRIC CHARGES AND FIELDS -SECTION B NUMERICALS (ADDITONAL EXERCISE)

Home
Ask Doubt
Profile