Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss's law. [Hint. use Coulomb's law directly and evaluate the necessary integral].
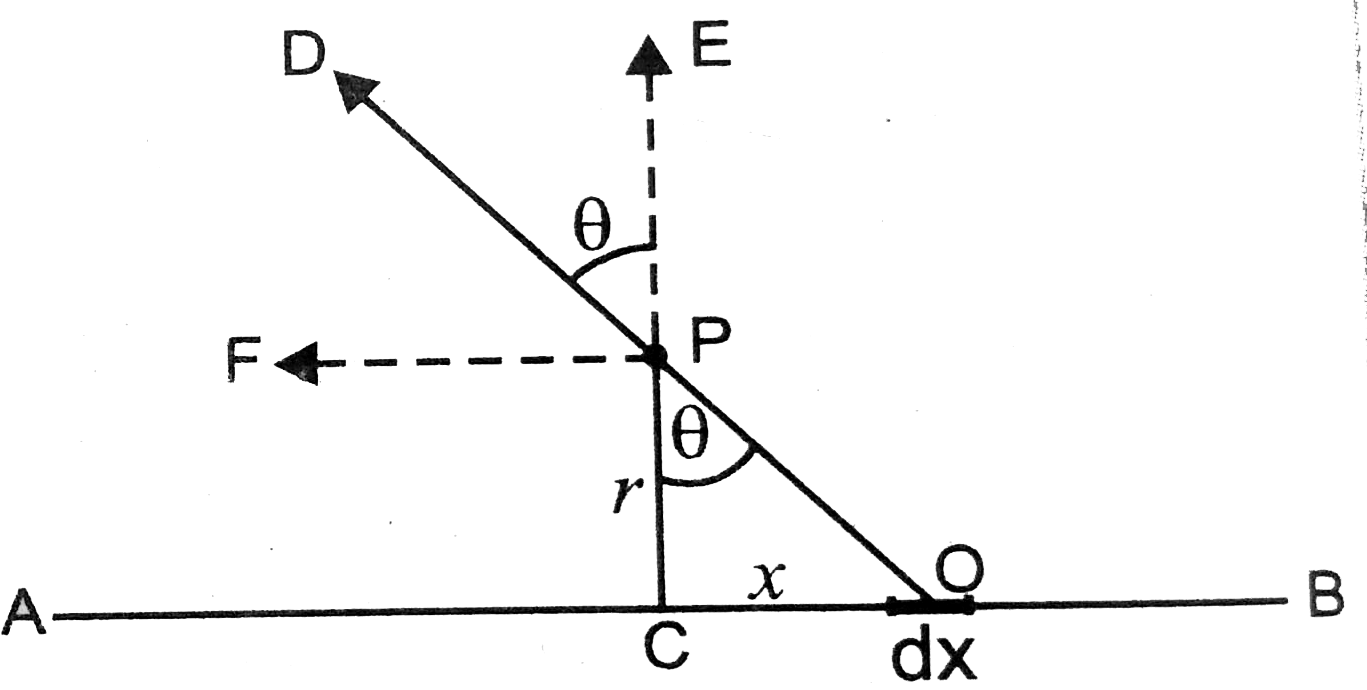
In Fig, AB is a long thin wire of uniform linear charge density, λ. We have to obtain formula for electric field due to this wire at any point P at a perpendicular distnace PC=r form the wire.
Consider a small element of length, dx of the wire with center 0, such that OC=x
Charge on the element, q=λdx
∴ Electric intensity at p due to the element,
dE=14π∈0λdxOP2=λdx4π∈0(r2+x2)
−→dE is along OPD. If ∠OPC=0,−→dE can be resolved into two recantugular components : dE cos θ along PE⊥AB and dE sinθ along PF∣∣BA. The parallel components component will be cancelled by the parallel component of the field due to charge on a simillar element dx of wire on the other half. The radial component gets added.
∴ effective component of electric intensity due to the charge element, −→dE=dE=dEcosθ
dE=λdxcosθ4π∈0(r2+x2) ....(i)
From ΔOCP,x=rtanθ∴dx=rsec2θdθ
Now, r2+x2=r2+r2tan2θ=r2(1+tan2θ)=r2sec2θ
From (i), dE'=λrsec2θdθ4π∈0r2sec2θcosθ=λ4π∈0rcosθdθ
As wire has infinite length, its ends A and B are infinite distance apart. Therefore, θ varies from −π/2→+π/2 :. Electric intensity at P due to the whole wire,
E'∫π/2−π/2λ4π∈0rcosθdθ=λ4π∈0r[sinθ]π/2−π/2=λ2π∈0r
Similar Questions
Knowledge Check
The electric field intensity due to a thin infinity long straight wire of uniform linear charge density λ at O is-
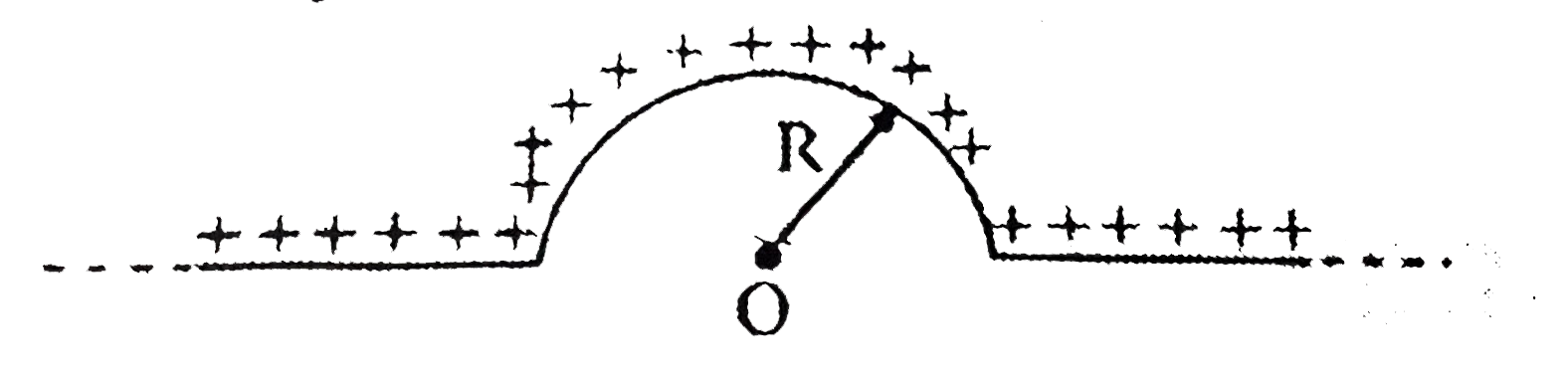 Aλ2πε0RBλ√22πε0RCλ√52πε0RDzero
Aλ2πε0RBλ√22πε0RCλ√52πε0RDzeroTwelve infinite long wire of uniform linear charge density (λ) are passing along the twelve edges of a cube. Find electric flux through any face of cube. ,
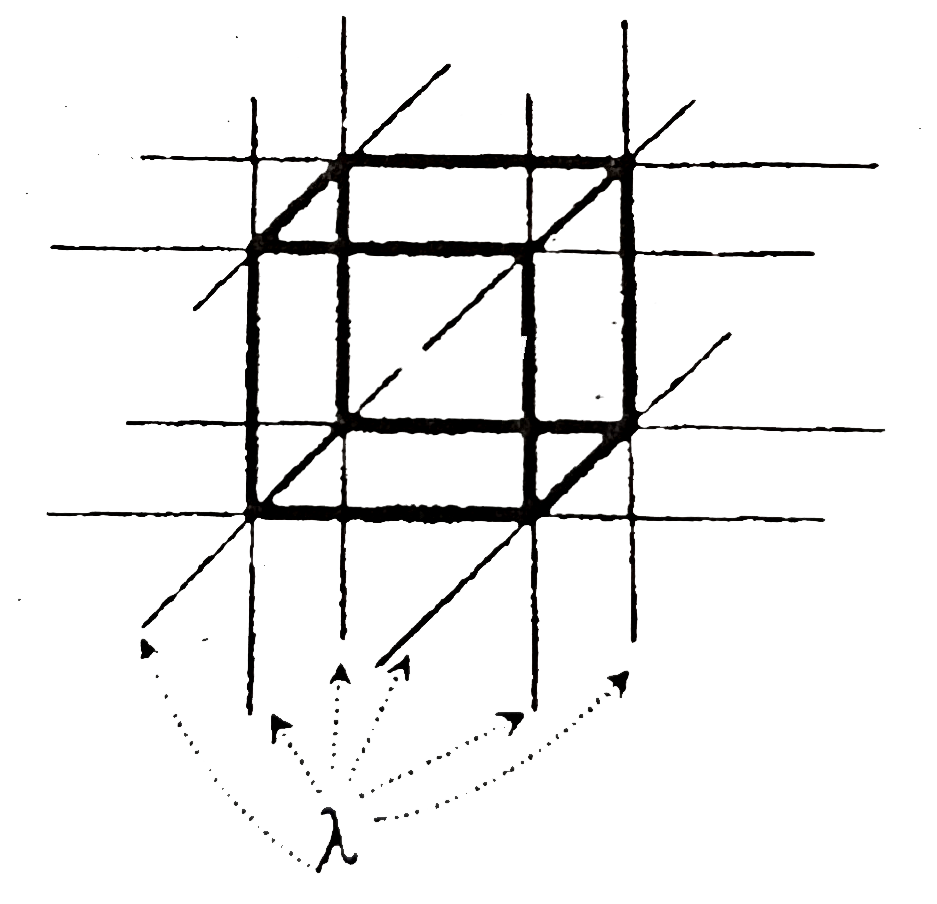 A(λl2ε0)B(λlε0)C(λl3ε0)D(3λlε0)
A(λl2ε0)B(λlε0)C(λl3ε0)D(3λlε0)The electric field strength due to a circular loop of charge of radius R are uniform linear density of charge λ, at its centre is proportonal to
AλRBλ/RCλ/R2DNone of these
Write the expression of electric field due to an infinitely long, straight, wire having linear charge density λ at a point that is at a distance r from it.
View SolutionState Gauss' law.Using this law obtain the expression for the electric field due to an infinitely long straight conductor of linear charge density λ
(ii) A wire AB of length L has linear charge λ=kx, where x is measured from the end A of the wire. The wire is enclosed by a Gaussian hollow surface.Find the expression for the electric flux through the surface.
View SolutionCalculation OF electric field using gauss law
View Solution(a) State Gauss's law. Using this law, obtain the expression for the electric field due to an infinitely long straight conductor of linear charge desntiy λ.
(b) A wire AB of length L has linear charge density λ=kx, where x is measured from the end A of the wire.
This wire is enclosed by a Gaussian hollow surface. Find the expression for the electric flux through this surface.
View SolutionIn the given arrangement find the electric field at C in the figure. Here the U-shaped wire is uniformly charged with linear charge density λ. [0]
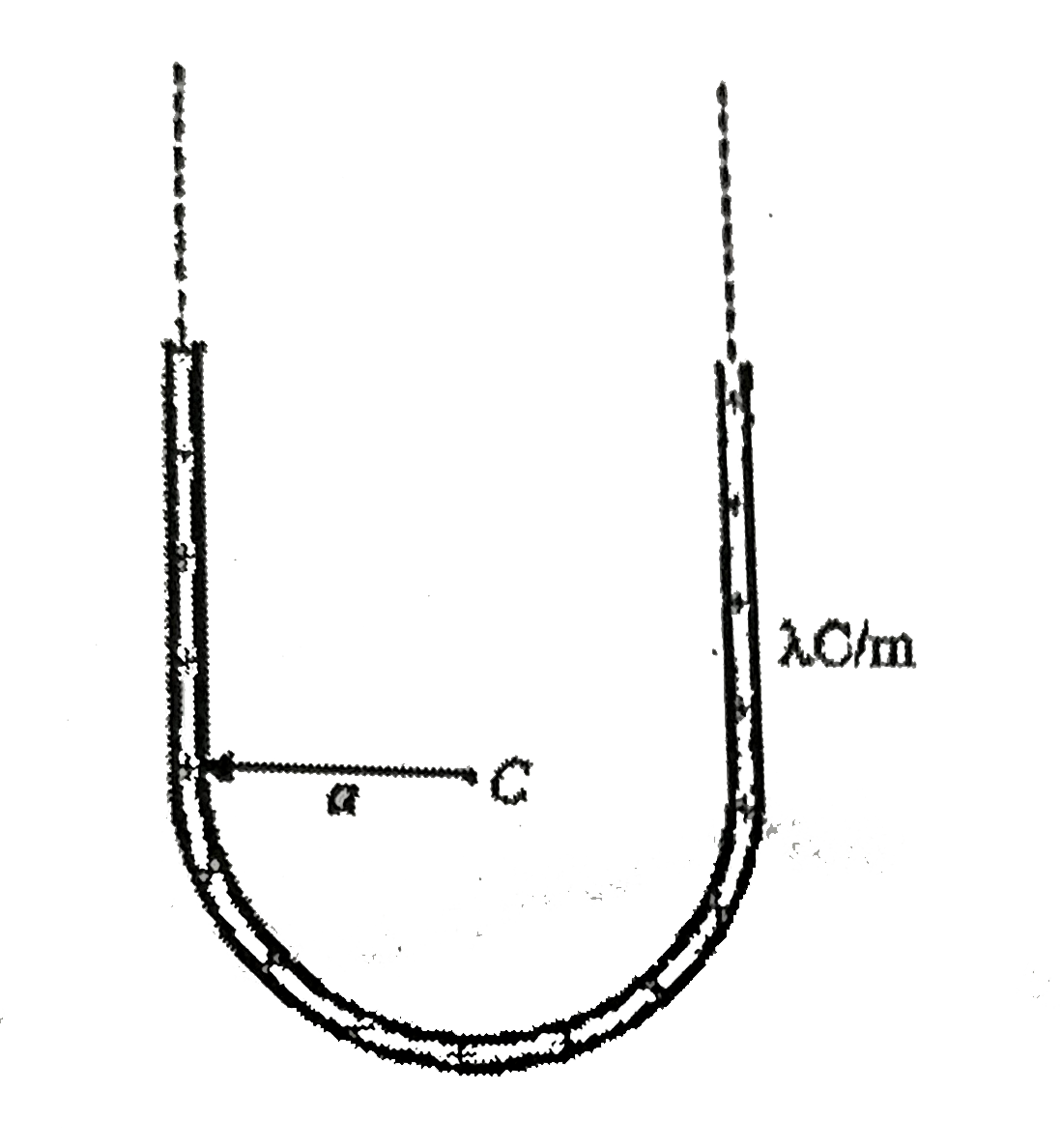
View Solution


