गाउस नियम का उपयोग किए बिना किइस एकसमान रैखिक आवेश घनत्व λ के लम्बे पतले तार के कारण विधुत क्षेत्र के लिए सूत्र प्राप्त कीजिए। [संकेत - सीधे ही कूलॉम नियम का उपयोग करके आवश्यक समाकलन का मान निकालिए ]।
माना AB एक लम्बा पतला तार है जिस पर रैखिक आवेश घनत्व λ है। उससे r दुरी पर एक बिंदु P है जिस पर विधुत क्षेत्र के लिए सूत्र ज्ञात करना है।
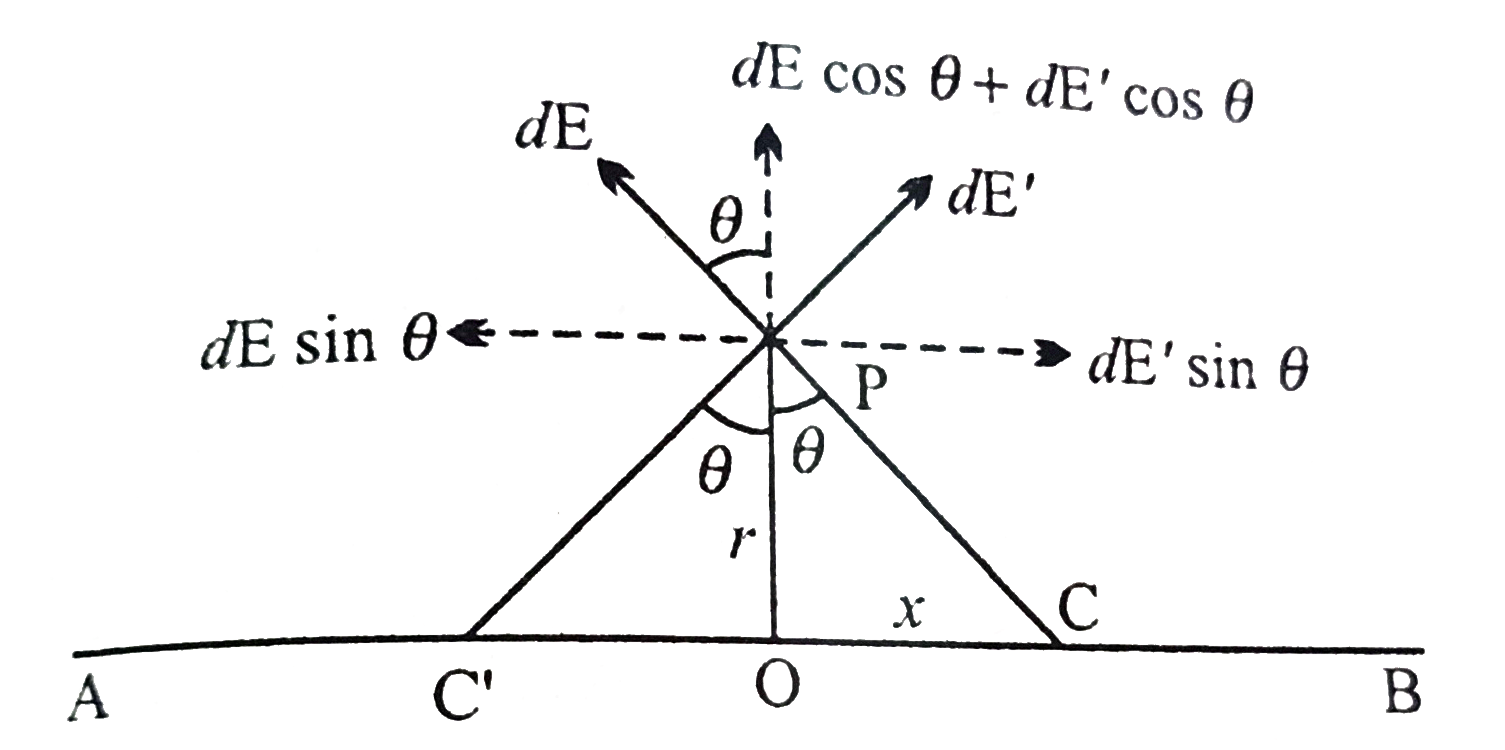
O से x दुरी पर dx लम्बाई के एक अल्पांश C कि कल्पना करे। अल्पांश C पर कुल आवेश
q=λdx ...(1)
अल्पांश C के आवेश के कारण बिंदु P पर विधुत क्षेत्र dE=14πε0.qCP2, इसकी दिशा −−→CP के अनुदिश होगी।
समी (1 ) से मान रखने पर,
de=14πε0.λdxCP2
दे को दो घटको में वियोजित किया जा सकता है -
(i)dEcosθ के अनुदिश
(ii) dEsinθ,OP के लंबवत
बिंदु O के विपरीत और उतनी ही दुरी x पर dx लम्बाई के एक-दूसरे अल्पांश C ' कि कल्पना करे, तो इस अल्पांश के कारण बिंदु P पर विधुत क्षेत्र
dE'14πε0.qC'P2, इसकी दिशा →CP के अनुदिश होगी।
इसे भी दो घटको में वियोजित किया जा सकता है -
(i) dE'cosθ,OP के अनुदिश
(ii) dE'sinθOP के लंबवत
किन्तु CP=C'P, अतः OP के लंबवत घातक एक-दूसरे को निरस्त कर देंगे तथा OP के अनुदिश घातक आपस में जुड़ जायेगे। इसी प्रकार यदि बिंदु O के दोनों और समान दुरी पर समान लम्बाई के अल्पांश कि कल्पना करे तो समस्त अल्पाँशो के कारण OP के लंबवत घातक एक-दूसरे को निरस्त कर देंगे किंदु OP के अनुदिश घटक आपस में जुड़ जाएंग।
अतः बिंदु P पर परिणामी विधुत क्षेत्र
E=∫dEcosθ
=∫14πε0.λdxCP2cosθ, [समी (2 ) से]
=λ4πε0.∫dx.cosθr2+x2
किन्तु CP2=r2+x2
∴E=λ4πε0∫dx.cosθr2+x2 ...(3)
ΔPCO में tanθ=xr
या x=rtanθ
⇒dx=rsec2θdθ
तथा r2+x2=r2+r2tan2θ=r2(1+tan2θ)=r2sec2θ
समी (3 ) में मान रखने पर, E=λ4πε0∫rsec2dθ.cosθr2sec2θ
या E=λ4πε0.∫cosθdθr
यदि ताल लम्बा है तो, θ का मान −π2 से π2 पर परिवर्तित होगा।
∴E=λ4πε0∫π2−π2cosθdθr
=λ4πε0r[sinθ]π2−π2
=λ4πε0r[sinπ2−sin(−π2)]
=λ4πε0r(1+1)=λ2πε0r
यही अभीष्ट सूत्र है।
Topper's Solved these Questions
- BOOK - NAVBODHCHAPTER - वैधुत आवेश और क्षेत्र EXERCISE - बहुविकल्पीय प्रश्न प्लस49videos
वैधुत आवेश और क्षेत्र
- BOOK - NAVBODHCHAPTER - वैद्युत आवेश तथा क्षेत्रEXERCISE - तथ्यात्मक प्रश्न12videos
वैद्युत आवेश तथा क्षेत्र
- BOOK - NAVBODHCHAPTER - संचार व्यवस्था EXERCISE - NCERT पाठ्य पुस्तक के प्रश्नोत्तर9videos
संचार व्यवस्था
Similar Questions
एक आवेश q को L लम्बाई के घन के केंद्र O पर रखा गया है। एकसमान आवेश q केंद्र O से L दुरी पर रखा गया है। फलक ABCD से गुजरने वाला वैधुत फ्लक्स होगा -
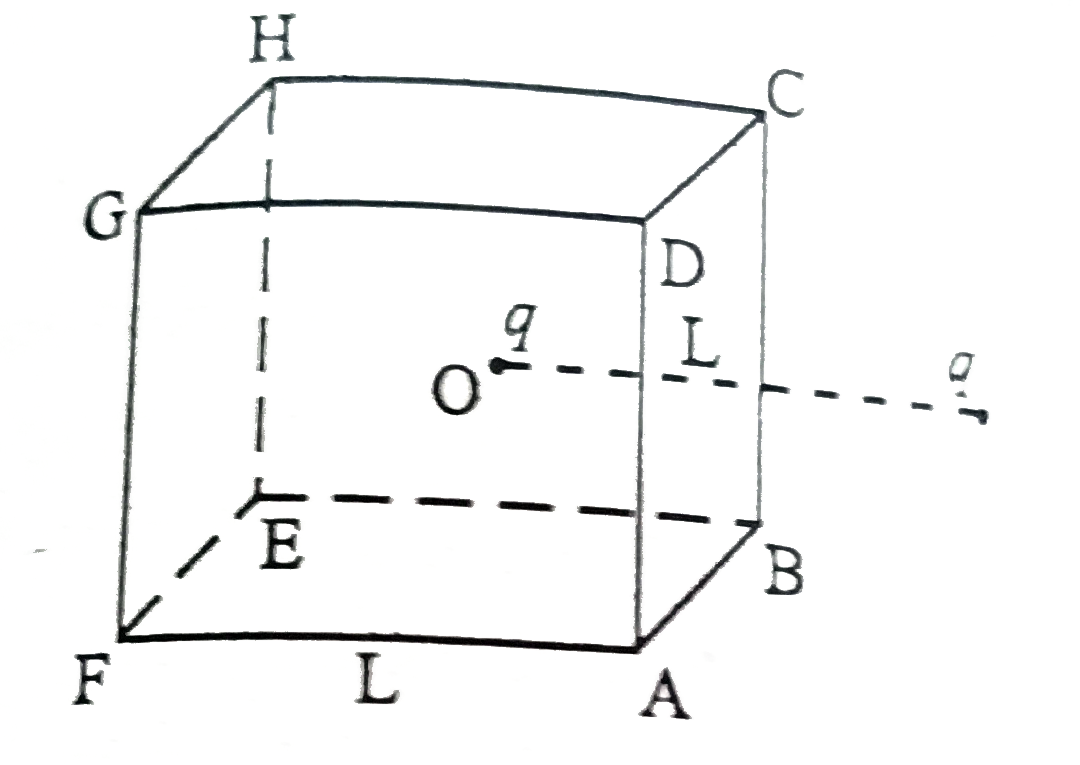 47:35View Solution
47:35View Solutionसामान्य विधूतरोधी होता है , किन्तु वायुयान के रबर टायर कुछ चालक बनाये जाते है , क्यों ?
53:12View Solutionव्योम तरंगो के उपयोग द्वारा क्षितिज के पार संचार के लिए निम्नलिखित अवृत्तयियो में से कोण -सी आवृतिया उपयुक्त रहेगी -
57:42View Solutionअनंत लंबाई के एकसमान आवेशित सीधे तार के कारण विद्युत क्षेत्र || कुछ प्रश्न
01:24:57View Solutionअनंत लंबाई के एकसमान आवेशित सीधे तार के कारण विद्युत क्षेत्र
47:38View Solutionविधुत धारा || धारा घनत्व || ओम का नियम || ओम के नियम की सीमाएँ
58:55View Solutionकूलॉम का नियम |कूलॉम के नियम का सदिश रूप |OMR|Summary
01:04:50View Solutionराउलट का नियम#!#राउलट के नियम के उपयोग#!#डेल्टन का नियम#!#वाष्प अवस्था में मोल अंश
44:14View Solutionकूलॉम के नियम का सदिश रूप | माध्यम में कूलॉम का नियम
01:07:37View Solutionबायोट-सावर्ट का नियम | एक सीधे तार के कारण चुंबकीय क्षेत्र का परिचय
01:09:57View Solutionआवेश का वितरण कितने प्रकार का होता है #!#रेखीये आवेशित चालक तार के कारण विधुत क्षेत्र की तीव्रता
40:44View Solutionगाउस का नियम|गाउस के नियम के अनुप्रयोग|ठोस चालक अथवा खोखले गोले के कारण विद्युत् क्षेत्र|OMR |Summary
01:15:27View Solutionकूलॉम के नियम पर आधारित प्रश्न |आवेश घनत्व के प्रकार |प्रश्न |विद्धुत क्षेत्र |OMR|Summary
01:20:43View Solutionविधुत फ्लक्स #!#गाउस का नियम
View Solutionगाउस के नियम का अनुप्रयोग
07:10View Solutionविधुत फ्लक्स #!#गॉस का नियम #!#गॉस के नियम के अनुप्रयोग
34:57View Solution

