A skier leaves the top of a slope with an initial speed of 5.0 m/s. Her speed at the bottom of the slope is 13 m/s. What is the height of the slope ?
1.1m
4.6m
6.4m
7.3m
The correct Answer is:D
To find the height of the slope that the skier descends, we can use the principle of conservation of energy, specifically the work-energy theorem. This theorem states that the work done by the forces acting on an object is equal to the change in its kinetic energy.
1. Identify Given Values:
- Initial speed of the skier, vi=5.0m/s
- Final speed of the skier, vf=13.0m/s
- Acceleration due to gravity, g=9.8m/s2
2. Write the Work-Energy Theorem:
The work done by gravity is equal to the change in kinetic energy:
W=ΔKE=KEf−KEi
where KE=12mv2.
3. Calculate the Initial and Final Kinetic Energies:
- Initial kinetic energy, KEi=12mv2i=12m(5.0)2=12m(25)=12.5m
- Final kinetic energy, KEf=12mv2f=12m(13.0)2=12m(169)=84.5m
4. Calculate the Change in Kinetic Energy:
ΔKE=KEf−KEi=84.5m−12.5m=72m
5. Set Up the Equation for Work Done by Gravity:
The work done by gravity can also be expressed as:
W=mgh
where h is the height of the slope.
6. Equate the Work Done to the Change in Kinetic Energy:
mgh=72m
We can cancel m from both sides (assuming m≠0):
gh=72
7. Solve for Height h:
h=72g=729.8
h≈7.35m
Final Answer:
The height of the slope is approximately 7.35m.
- Initial speed of the skier, vi=5.0m/s
- Final speed of the skier, vf=13.0m/s
- Acceleration due to gravity, g=9.8m/s2
The work done by gravity is equal to the change in kinetic energy:
W=ΔKE=KEf−KEi
where KE=12mv2.
- Initial kinetic energy, KEi=12mv2i=12m(5.0)2=12m(25)=12.5m
- Final kinetic energy, KEf=12mv2f=12m(13.0)2=12m(169)=84.5m
ΔKE=KEf−KEi=84.5m−12.5m=72m
The work done by gravity can also be expressed as:
W=mgh
where h is the height of the slope.
mgh=72m
We can cancel m from both sides (assuming m≠0):
gh=72
h=72g=729.8
h≈7.35m
The height of the slope is approximately 7.35m.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)
10 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
9 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PROBLEMS
58 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
A small ball is projected up a smooth inclined plane with an initial speed of 10m/s at 30∘ from the bottom edge of the slope. It returns to the edge after 2s. The ball is in contact with the inclined plane throughout the process. The inclination angle (in degree) of the plane is N. The value of N/6 is
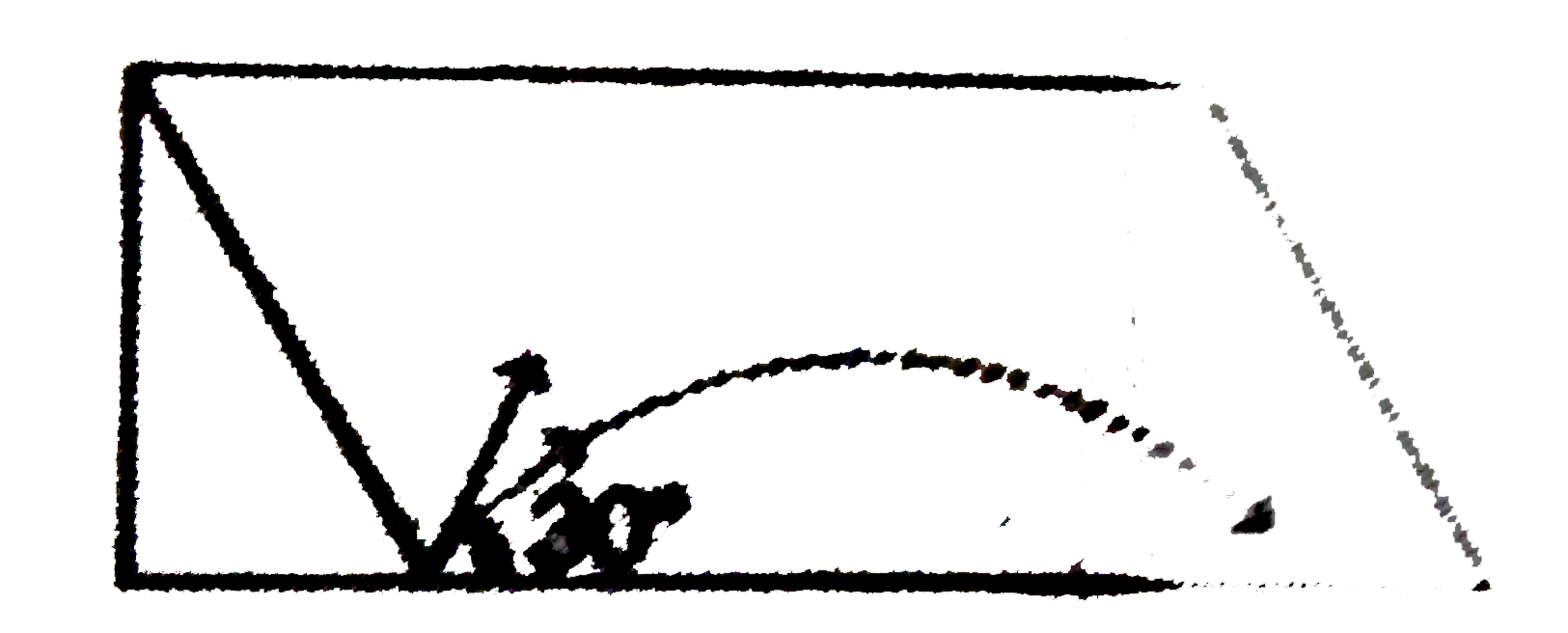
View SolutionWhat kind of energy does the skier have at the top of the slope?
View Solution
Knowledge Check
A small ball is projected up a smooth inclined plane with an initial speed of 10m/s along the direction at 30∘ to the bottom edge of the slope. It returns to the edge after 2s. The ball is in constant with the inclined plane throughout the process. What is the inclination angle of the plane?
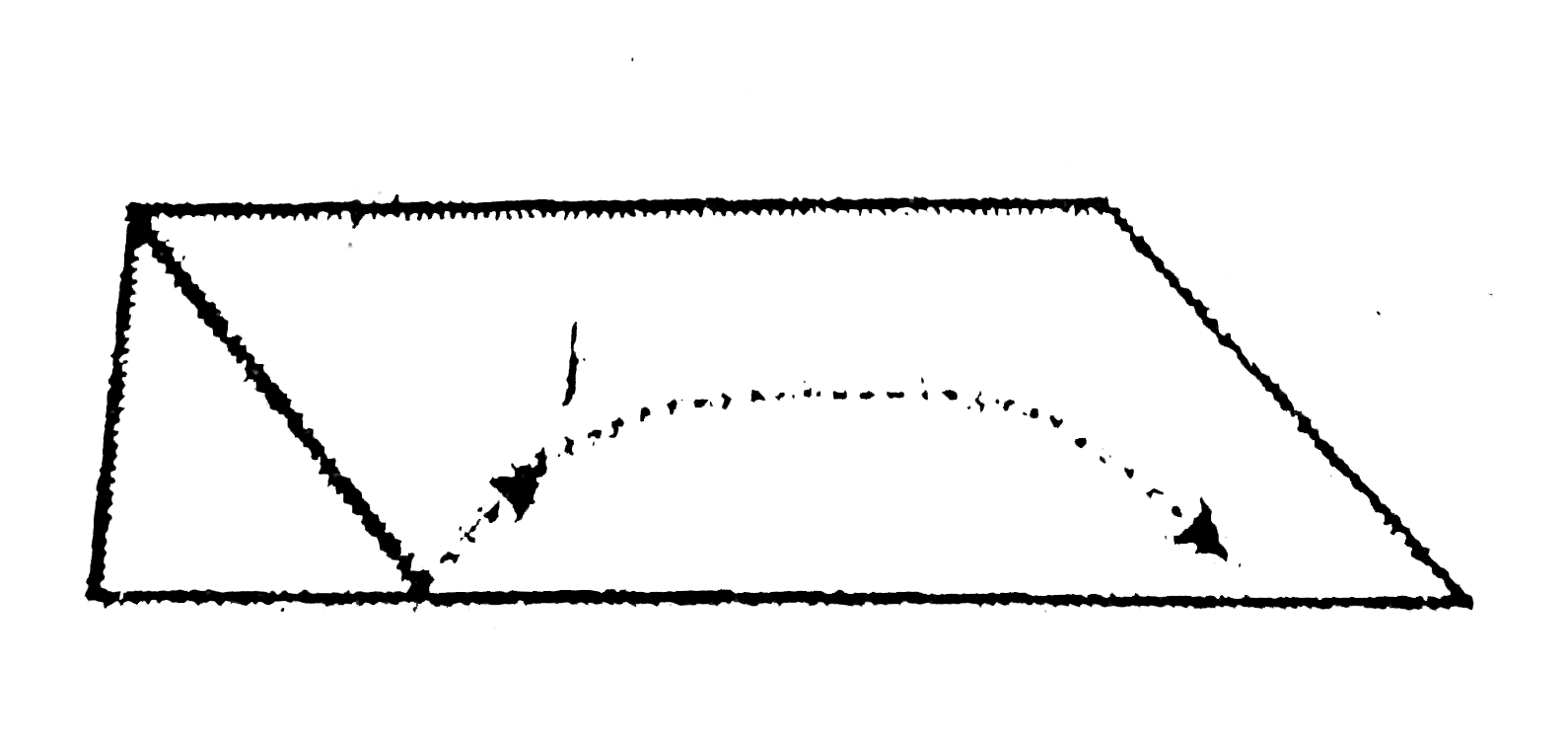 A15∘B60∘C37∘D30∘
A15∘B60∘C37∘D30∘A small ball is projected up a smooth inclined plane with an initial speed of 10m/s along the direction at 30∘to the bottom edge of the slope .It returns to the edge after 2s . The ball is in contact with the inclied plane throughout the process. The angle of inclination θ is :−.
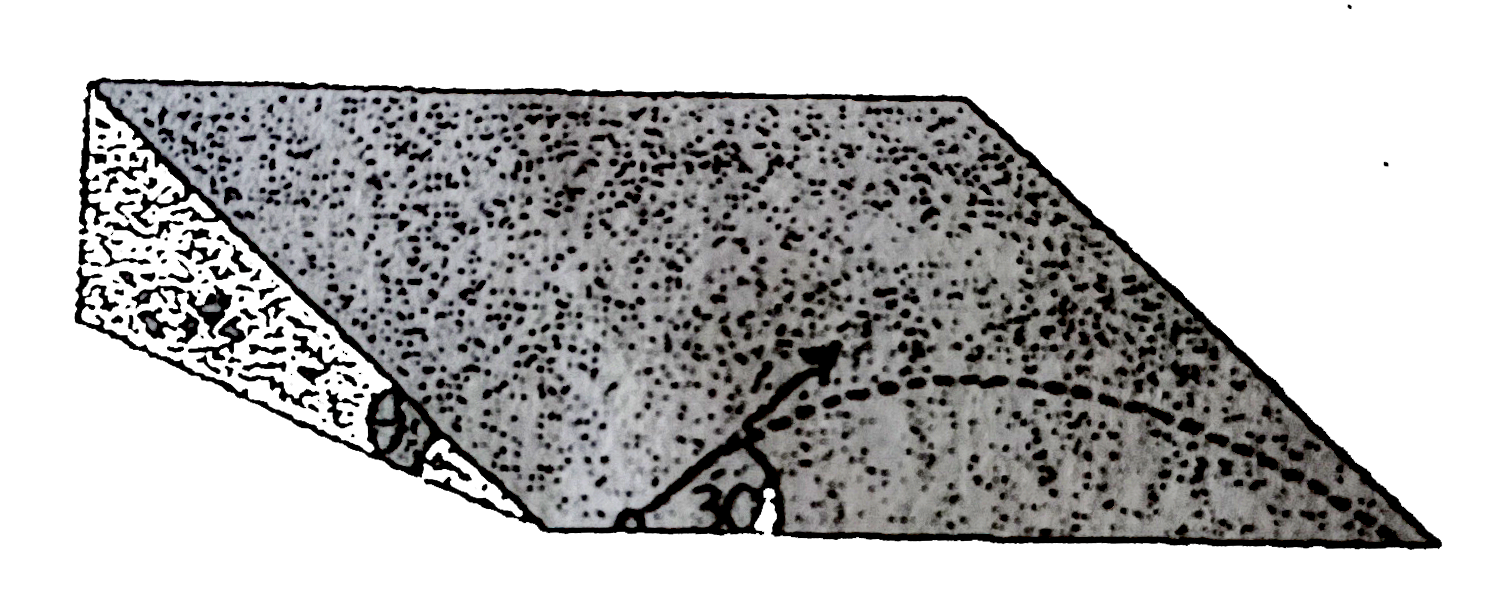 A45∘B53∘C30∘D37∘
A45∘B53∘C30∘D37∘A block of mass m is released from the top of a mooth inclined plane of height h its speed at the bottom of the plane is proportion to
Am0BmCm2Dm−1
A rock is thrown downward from an unknown height above the ground with an initial speed of 10 m/s. It strikes the ground 3.0 s later. Determine the initial height of the rock above the ground .
View SolutionA projectivle is fired form the top of a 40 m hnigh cliff with an initial speed of 50 m/s at an unknown angle. Find its speed when it hits the ground.
View SolutionA stone is thrown vertically upwards from the top of a building, with a speed of 14.7m/s. if it returns to the earth in 8s, calculate the height of the building.
View SolutionA skier is pulled by towrope up frictionless ski slope that makes an angle of 12∘ with the horizontal . The rope moves parallel to the slope with a constant speed of 1.0 m/s. The force of the rope does 880 J of work on the skier as the skier moves a distance of 7.0 m up the incline. (a) If the rope moved with a constant speed of 2.0 m/s, how much work would the force of the rope do on the skier as the skier moved a distance of 8.0 m up the incline ? At what rate is the force of the rope doing work on the skier when the rope moves with a speed of (b) 1.0 m/s and (c) 2.0 m/s ?
View SolutionWhat does the slope of a speed-time graph indicate ?
View Solution
