A rock is thrown downward from an unknown height above the ground with an initial speed of 10 m/s. It strikes the ground 3.0 s later. Determine the initial height of the rock above the ground .
The correct Answer is:74 m
To determine the initial height of the rock above the ground, we can use the equations of motion. Here's the step-by-step solution:
Step 1: Identify the known values
- Initial speed (u) = 10 m/s (downward)
- Time (t) = 3 s
- Acceleration (a) = g = 9.8 m/s² (downward)
Step 2: Set up the equation of motion
We will use the second equation of motion:
s=ut+12at2
where:
- s is the displacement (which will be the height h but taken as negative since it's downward),
- u is the initial velocity,
- a is the acceleration,
- t is the time.
Step 3: Substitute the known values into the equation
Since the rock is thrown downward, we take downward as negative:
- u=−10m/s
- a=−9.8m/s2
- t=3s
Substituting these values into the equation:
−h=(−10)(3)+12(−9.8)(32)
Step 4: Calculate the displacement
Calculating each term:
1. −10×3=−30
2. 12×−9.8×9=−44.1
Now, substituting these values back into the equation:
−h=−30−44.1
−h=−74.1
Step 5: Solve for height
To find h:
h=74.1m
Final Answer
The initial height of the rock above the ground is 74.1 meters.
---
- Initial speed (u) = 10 m/s (downward)
- Time (t) = 3 s
- Acceleration (a) = g = 9.8 m/s² (downward)
We will use the second equation of motion:
s=ut+12at2
where:
- s is the displacement (which will be the height h but taken as negative since it's downward),
- u is the initial velocity,
- a is the acceleration,
- t is the time.
Since the rock is thrown downward, we take downward as negative:
- u=−10m/s
- a=−9.8m/s2
- t=3s
−h=(−10)(3)+12(−9.8)(32)
Calculating each term:
1. −10×3=−30
2. 12×−9.8×9=−44.1
−h=−30−44.1
−h=−74.1
To find h:
h=74.1m
The initial height of the rock above the ground is 74.1 meters.
Topper's Solved these Questions
- MOTION ALONG A STRAIGHT LINEBook:RESNICK AND HALLIDAYChapter:MOTION ALONG A STRAIGHT LINEExercise:PRACTICE QUESTIONS ( Single Correct Choice Type)
Explore 54 Videos
- MOTION ALONG A STRAIGHT LINEBook:RESNICK AND HALLIDAYChapter:MOTION ALONG A STRAIGHT LINEExercise:PRACTICE QUESTIONS ( More than One Correct Choice Type )
Explore 6 Videos
- MOTION ALONG A STRAIGHT LINEBook:RESNICK AND HALLIDAYChapter:MOTION ALONG A STRAIGHT LINEExercise:Checkpoints
Explore 5 Videos
- MAGNETIC FORCEBook:RESNICK AND HALLIDAYChapter:MAGNETIC FORCEExercise:Practice Questions (Integer type )
Explore 7 Videos
- MOTION IN TWO AND THREE DIMENSIONSBook:RESNICK AND HALLIDAYChapter:MOTION IN TWO AND THREE DIMENSIONSExercise:PRACTICE QUESTIONS (MATRIX-MATCH)
Explore 10 Videos
Similar Questions
A block of mass m is dropped from height h above the ground. Find out the speed of the block when it reaches the ground.
View SolutionA ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find a. the time it takes to reach the ground, b. the horiontal distance it travels before reaching the ground, c. the velocity (direction and magnitude) with which it strikes the ground.
View Solution
Knowledge Check
In the above problem, the initial speed with which water strikes the ground in ms−1 is
A10B5C5√2D10√2All the particles thrown with same initial velocity would strike the ground.
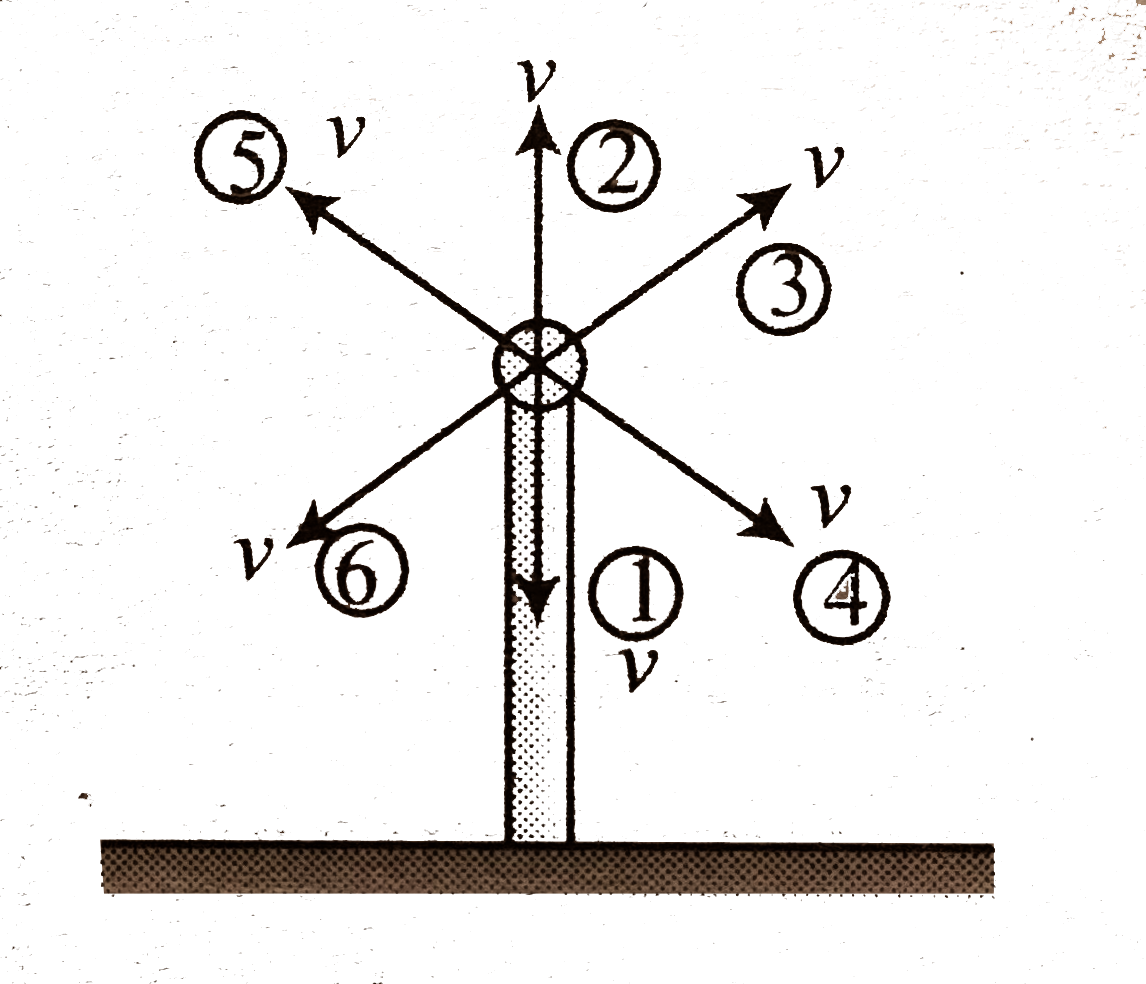 .Awith same speed.BsimultaneouslyCtime would be least for the particle thrown with velocity v downward i.e., particle 1.Dtime would be maximum for the particle 2.
.Awith same speed.BsimultaneouslyCtime would be least for the particle thrown with velocity v downward i.e., particle 1.Dtime would be maximum for the particle 2.A ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
A√2h/gB√8h/gC√u2+2ghgDug+√2hg
A ball is thrown horizontally from a point 100m above the ground with a speed of 20m/s. Find (a) the time it takes to reach the ground, (b) the horizontal distance it travels before reaching the ground, (c) the velocity (direction and magnitude) with which it strikes the ground.
View SolutionA ball is thrown straight upward with a speed v from a point h meter above the ground. The time taken for the ball to strike the ground is
View SolutionAn arrow is shot horizontally from a height of 4.9 m above the ground. The initial speed of the arrow is 45 m/s. Neglecting friction, how long will it take the arrow to hit the ground?
View SolutionA body thrown horizontally from the top of a building with a speed 20m/s, strikes the ground 40m away from the foot of tower. The height of the tower is
View SolutionA stone is thrown from the top of a tower at an angle of 30∘ above the horizontal level with a velocity of 40 m/s. it strikes the ground after 5 second from the time of projection then the height of the tower is
View Solution