A 1900-kg car experiences a combined force of air resistance and friction that has the same magnitude whether the car goes up or down a hill at 27 m/s. Going up a hill, the car's engine needs to produce 47 hp more power to sustain the constant velocity than it does going down the same hill. At what angle is the hill inclined above the horizontal ?
1.4∘
2.5∘
1.1∘
2.0∘
The correct Answer is:D
To solve the problem, we need to determine the angle of inclination of the hill (θ) based on the power difference required when the car is moving uphill versus downhill. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Forces Acting on the Car
When the car is moving uphill, the forces acting on it include:
- The gravitational force component acting down the slope: mgsinθ
- The friction and air resistance force FR acting opposite to the direction of motion.
When the car is moving downhill, the forces acting on it include:
- The gravitational force component acting down the slope: mgsinθ
- The friction and air resistance force FR acting up the slope.
Step 2: Write the Equations for Power
The power required to move the car uphill (P1) and downhill (P2) can be expressed as:
- P1=(FR+mgsinθ)⋅V
- P2=(mgsinθ−FR)⋅V
Where:
- V=27m/s (the constant velocity of the car)
Step 3: Set Up the Power Difference Equation
According to the problem, the power difference when going uphill and downhill is given as:
P1−P2=47hp
Converting horsepower to watts:
47hp=47×746W=35022W
Substituting the expressions for P1 and P2:
(FR+mgsinθ)⋅V−(mgsinθ−FR)⋅V=35022
Step 4: Simplify the Equation
Expanding and simplifying the equation:
FRV+mgsinθV−mgsinθV+FRV=35022
2FRV=35022
Thus, we can express FR:
FR=350222V
Step 5: Substitute Values
Substituting V=27m/s:
FR=350222×27=3502254≈648.5N
Step 6: Relate Forces to Find θ
Now, we can relate FR to the angle of inclination:
Using the equation for the forces when the car is going uphill:
FR+mgsinθ=0
Thus:
mgsinθ=FR
Substituting FR:
mgsinθ=648.5
Step 7: Solve for sin θ
Substituting m=1900kg and g=9.8m/s2:
1900⋅9.8⋅sinθ=648.5
sinθ=648.51900⋅9.8
Calculating:
sinθ=648.518620≈0.0348
Step 8: Find θ
Taking the inverse sine:
θ=sin−1(0.0348)≈2.0∘
Final Answer
The angle of inclination of the hill above the horizontal is approximately 2 degrees.
---
When the car is moving uphill, the forces acting on it include:
- The gravitational force component acting down the slope: mgsinθ
- The friction and air resistance force FR acting opposite to the direction of motion.
- The gravitational force component acting down the slope: mgsinθ
- The friction and air resistance force FR acting up the slope.
The power required to move the car uphill (P1) and downhill (P2) can be expressed as:
- P1=(FR+mgsinθ)⋅V
- P2=(mgsinθ−FR)⋅V
- V=27m/s (the constant velocity of the car)
According to the problem, the power difference when going uphill and downhill is given as:
P1−P2=47hp
Converting horsepower to watts:
47hp=47×746W=35022W
(FR+mgsinθ)⋅V−(mgsinθ−FR)⋅V=35022
Expanding and simplifying the equation:
FRV+mgsinθV−mgsinθV+FRV=35022
2FRV=35022
Thus, we can express FR:
FR=350222V
Substituting V=27m/s:
FR=350222×27=3502254≈648.5N
Now, we can relate FR to the angle of inclination:
Using the equation for the forces when the car is going uphill:
FR+mgsinθ=0
Thus:
mgsinθ=FR
Substituting FR:
mgsinθ=648.5
Substituting m=1900kg and g=9.8m/s2:
1900⋅9.8⋅sinθ=648.5
sinθ=648.51900⋅9.8
Calculating:
sinθ=648.518620≈0.0348
Taking the inverse sine:
θ=sin−1(0.0348)≈2.0∘
The angle of inclination of the hill above the horizontal is approximately 2 degrees.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)
10 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
9 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PROBLEMS
58 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
A compact car travelling at 27m/s on a level highway experiences a frictional force of 300 N due to air resistance and the friction of types with the road. What is the horse power of the engine of the car ?
View SolutionA car of mass m 1600 kg, while moving on any road, experience resistance to its motion given by (m+nV2) newton, where m and n are positive constants. On a horizontal road the car moved at a constant speed of 40 m/s when the engine developed a power of 53 KW. When the engine developed an output of 2 KW the car was able to travel on a horizontal road at a constant speed of 10 m/s. (a) Find the power that the engine must deliver for the car to travel at a constant speed of 40 m/s on a horizontal road. (b) The car is able to climb a hill at a constant speed of 40 m/s with its engine working at a constant rate of 69 KW. Calculate the inclination of the hill (in degree)
View Solution
Knowledge Check
A 63-kg skier goes up a snow-convered hill that makes an angle of 25∘ with the horizontal . The initial speed of the skier is 6.6 m/s. After coasting a distance of 1.9 m up the slope, the speed of the skier is 4.4 m/s. Find the work done by the kinetic frictional force that acts on the skis .
A−760JB+270JC+300JD−270J
The conducting rod shown in Fig. 30-37 has length Land is being pulled along horizontal, frictionless conducting rails at a constant velocity →v. The rails are connected at one end with a metal strip. A uniform magnetic field →B, directed out of the page, fills the region in which the rod moves. Assume that L = 10 cm, v = 5.0 m/s, and B = 1.2 T. What are the (a) magnitude and (b) direction (up or down the page) of the emf induced in the rod? What are the (c) size and (d) direction of the current in the conducting loop? Assume that the resistance of the rod is 0.40 Ω and that the resistance of the rails and metal strip is negligibly small. (e) At what rate is thermal energy being generated in the rod? (f) What external force on the rod is needed to maintain →v? (g) At what rate does this force do work on the rod?
View SolutionA truck of mass M has 4 wheels. The surface area of the metal disc in each wheel is A. When brakes are applied the brake shoe in each wheel rubs against the metal disc. This produces heat. We will assume that this heat is used to heat the disc in the wheel only. Each disc has mass m and is made of material of specific heat capacity s. One day the truck was going downhill on a road inclined at angle θ to the horizontal. To maintain a constant speed v the driver had to apply brakes. The only other dissipative force, apart from the brake force, on the truck is the air resistance force that is equal to F. Assume no heating of discs due to air friction.
(a) Find the initial rate of rise of temperature of each metal disc after the brakes are applied.
(b) Find the final temperature (T) of the disc assuming that it is a black body and it loses heat only through radia- tion. Take the atmospheric temperature to be T0
View SolutionIn Fig a car is driven at constant speed over a circular hill and then into a circular valley with the same radius. At the top of the hill, the normal force on the driver from the car seat is 0. The driver's mass is 80.0 kg. what is the magnitude of the normal force on the driver from the seat when the car passes through the bottom of the valley?
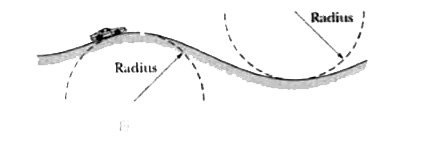
View SolutionA car weighing 1120kg is going up an incline of 1 in 56 at the rate of 20m in 2s. Find the power of the engine if frictional force is 64N.
View SolutionA truck can move up a road which has a gradient of 1 m rise every 50 m with a speed of 24 kmph ? How fast will the same truck move down the hill with the same horse power ? The air resistance to the motion of the truck is 1/25 of its weight.
View SolutionA car can pull a trailer of twice its mass up a certain slope at a maximum speed v=1m/s. Without the trailer the maximum speed of the car up the same slope is 2v. The resistance to the motion is proportinal to mass and square of speed. If the car (without trailer) starts to move down the same slope, with its engine shut off, eventually it will acquire a constant speed vt, then find v2t (in m2/s2)
View SolutionRam is a college student in Delhi. Ram and his family are going by car to visit a hill station. Ram himself is driving the car. Ram drives the car very carefully. Before starting to drive, Ram has fastened the car seat belt himself properly. He has also made his father, mother and younger brother fasten their car seat belts. on the flat highwat road, Ram is keeping the car speed within a range of 50 to 60 kmph (which is well within the prescribed speed limit on this highway). He does nto accelerate the car unnecessarily. After driving for about five hours continuously on a flat road, there is a sight of hills in view. On approaching the hilly road, Ram increases the speed of his car. Ram's younger brother Anish, who is a student of class VI, is surprised to see his brother increasing the speed of car suddenly. Anish asks Ram why the speed of car has been increased. Ram explains the reason for increasing the speed of car to everyone.
(a) What type of energy is possessed by the car while running on the flat road?
(b) What type of energy transformation take place in a car engine?
(c) When the car is moving on the flat road, it has to do work to overcome mainly two types of forces. Name these two types of forces.
(d) When the car is moving on an uphill road, it has to do work to overcome three types of forces. Name these three types of forces.
(e) Why does Ram increase the speed of his car on approaching the hilly road?
(f) What types of energy is possessed by the car going up on the hilly road?
(g) What values are displayed by Ram in this episode?
View Solution
