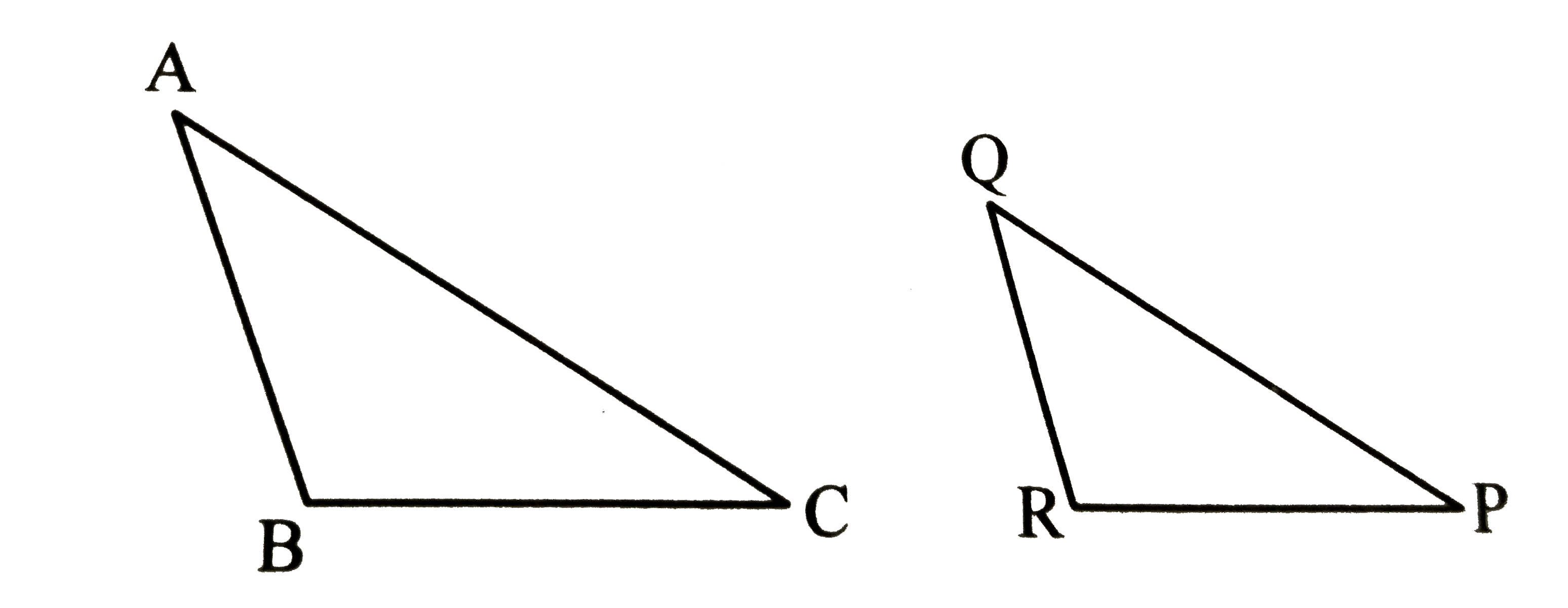
ΔABCandΔPQR are congruent under the correspondence : ABC↣RQP write the parts of ΔABC that correspond to ? (i) ¯¯¯¯¯¯PQ (ii) ∠Q (iii) ¯¯¯¯¯¯RP
To solve the problem, we need to identify the corresponding parts of triangle ABC based on the given correspondence of the triangles ABC and PQR, where ABC corresponds to RQP.
1. Identify the Correspondence:
- Given that triangle ABC is congruent to triangle RQP, we have the correspondence:
- A corresponds to R
- B corresponds to Q
- C corresponds to P
2. Find the Corresponding Part for ¯¯¯¯¯¯¯¯PQ:
- Since P corresponds to C and Q corresponds to B, the side ¯¯¯¯¯¯¯¯PQ corresponds to the side ¯¯¯¯¯¯¯¯BC in triangle ABC.
- Therefore, ¯¯¯¯¯¯¯¯PQ corresponds to ¯¯¯¯¯¯¯¯BC.
3. Find the Corresponding Part for ∠Q:
- From the correspondence, we know that angle Q corresponds to angle B in triangle ABC.
- Therefore, ∠Q corresponds to ∠B.
4. Find the Corresponding Part for ¯¯¯¯¯¯¯¯RP:
- Since R corresponds to A and P corresponds to C, the side ¯¯¯¯¯¯¯¯RP corresponds to the side ¯¯¯¯¯¯¯¯AC in triangle ABC.
- Therefore, ¯¯¯¯¯¯¯¯RP corresponds to ¯¯¯¯¯¯¯¯AC.
Final Correspondences:
- (i) ¯¯¯¯¯¯¯¯PQ corresponds to ¯¯¯¯¯¯¯¯BC
- (ii) ∠Q corresponds to ∠B
- (iii) ¯¯¯¯¯¯¯¯RP corresponds to ¯¯¯¯¯¯¯¯AC
- Given that triangle ABC is congruent to triangle RQP, we have the correspondence:
- A corresponds to R
- B corresponds to Q
- C corresponds to P
- Since P corresponds to C and Q corresponds to B, the side ¯¯¯¯¯¯¯¯PQ corresponds to the side ¯¯¯¯¯¯¯¯BC in triangle ABC.
- Therefore, ¯¯¯¯¯¯¯¯PQ corresponds to ¯¯¯¯¯¯¯¯BC.
- From the correspondence, we know that angle Q corresponds to angle B in triangle ABC.
- Therefore, ∠Q corresponds to ∠B.
- Since R corresponds to A and P corresponds to C, the side ¯¯¯¯¯¯¯¯RP corresponds to the side ¯¯¯¯¯¯¯¯AC in triangle ABC.
- Therefore, ¯¯¯¯¯¯¯¯RP corresponds to ¯¯¯¯¯¯¯¯AC.
- (i) ¯¯¯¯¯¯¯¯PQ corresponds to ¯¯¯¯¯¯¯¯BC
- (ii) ∠Q corresponds to ∠B
- (iii) ¯¯¯¯¯¯¯¯RP corresponds to ¯¯¯¯¯¯¯¯AC
Topper's Solved these Questions
Similar Questions
Knowledge Check
Fill in the blanks .
(i) In two similar triangles , ABC and PQR , if their corresponding altitudes AD and PS are in the ratio 4 : 9 , then ar(ΔABC):ar(ΔPQR)=¯¯¯¯¯¯(P) .
(ii) Area of an equilateral triangle described on the side of a square is ¯¯¯¯¯¯(O) the area of equilateral triangle described on its diagonal .
(iii) The altitude of an equilateral triangle with side 'a' equals oberline((R ))APQR16:81Twicea2BPQR4:9Half2aCPQR16:81Half√3a2DPQR4:9Twice√3a2
In ΔABCandΔPQR, in a one to one correspondence.
ABQR=BCPR=CAPQ, then
View SolutionIn ΔABC and ΔPQR , in a one-to-one correspondance ABQR=BCPR=CAPQ then……

View SolutionIf ΔABCandΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use ?
View SolutionIf ∆ABC ≅ ∆FED under the correspondence ABC ↔ FED, write all the corresponding congruent parts of the triangles
View SolutionWrite the real and imaginary parts of the following
(i) 7
(ii) 3i
(iii) √57i
View SolutionIf ΔABC~ΔDEF and AB:PQ=5:7 then write the ratio of A(ΔABC):A(ΔPQR).
View SolutionWhich of the following statements are true and which of them are false?
(i) All squares are congruent.
(ii) If two squares have equal areas, they are congruent.
(iii) If two figures have equal areas, they are congruent.
(iv) If two triangles are equal in area, they are congruent.
(v) If two sides and one angle of a triangle are equal to the corresponding two sides and angle of another triangle, the triangles are congruent.
(vi) If two angles and any side of a triangle are equal to the corresponding angles and the side of another triangle then the triangles are congruent.
(vii) If three angles of a triangle are equal to the corresponding angles of another triangle then the triangles are congruent.
(viii) If the hypotenuse and an acute angle of a right triangle are equal to the hypotenuse and the corresponding acute angle of another right triangle then the triangles are congruent.
(ix) If the hypotenuse of a right triangle is equal to the hypotenuse of another right triangle then the triangles are congruent.
View Solution
