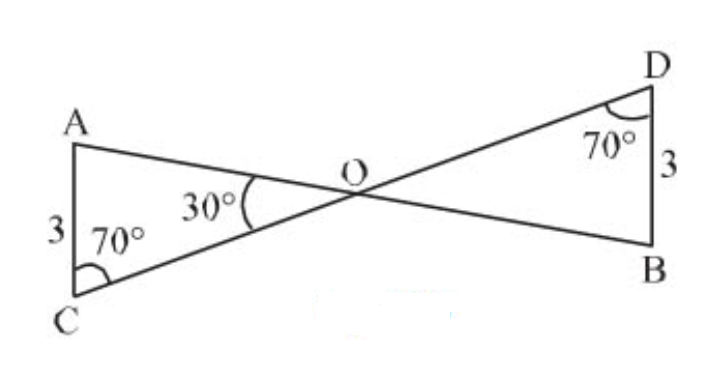
In the given figure, can you use ASA congruence rule and conclude that △AOC≅△BOD?
Video Solution
Text Solution
In the two triangles AOC and BOD, ∠C=∠D (each 70∘ )
Also, ∠AOC=∠BOD=30∘ (vertically opposite angles)
So, ∠A of △AOC=180∘–(70∘+30∘)=80∘
(using angle sum property of a triangle)
Similarly, ∠Bof△BOD=180∘–(70∘+30∘)=80∘
Thus, we have ∠A=∠B,AC=BD and ∠C=∠D
Now, side AC is between ∠A and ∠C and side BD is between ∠B and ∠D.
So, by ASA congruence rule, △AOC≅△BOD.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure, ΔRTQ≅ΔPSQ by ASA congruency condition. Which of the following pairs does not satisfy the condition.
 APQ=QRB∠P=∠RC∠TQP=∠SQRDNone of these
APQ=QRB∠P=∠RC∠TQP=∠SQRDNone of theseFrom the given P−T graph of CO2, you may conclude that it will be
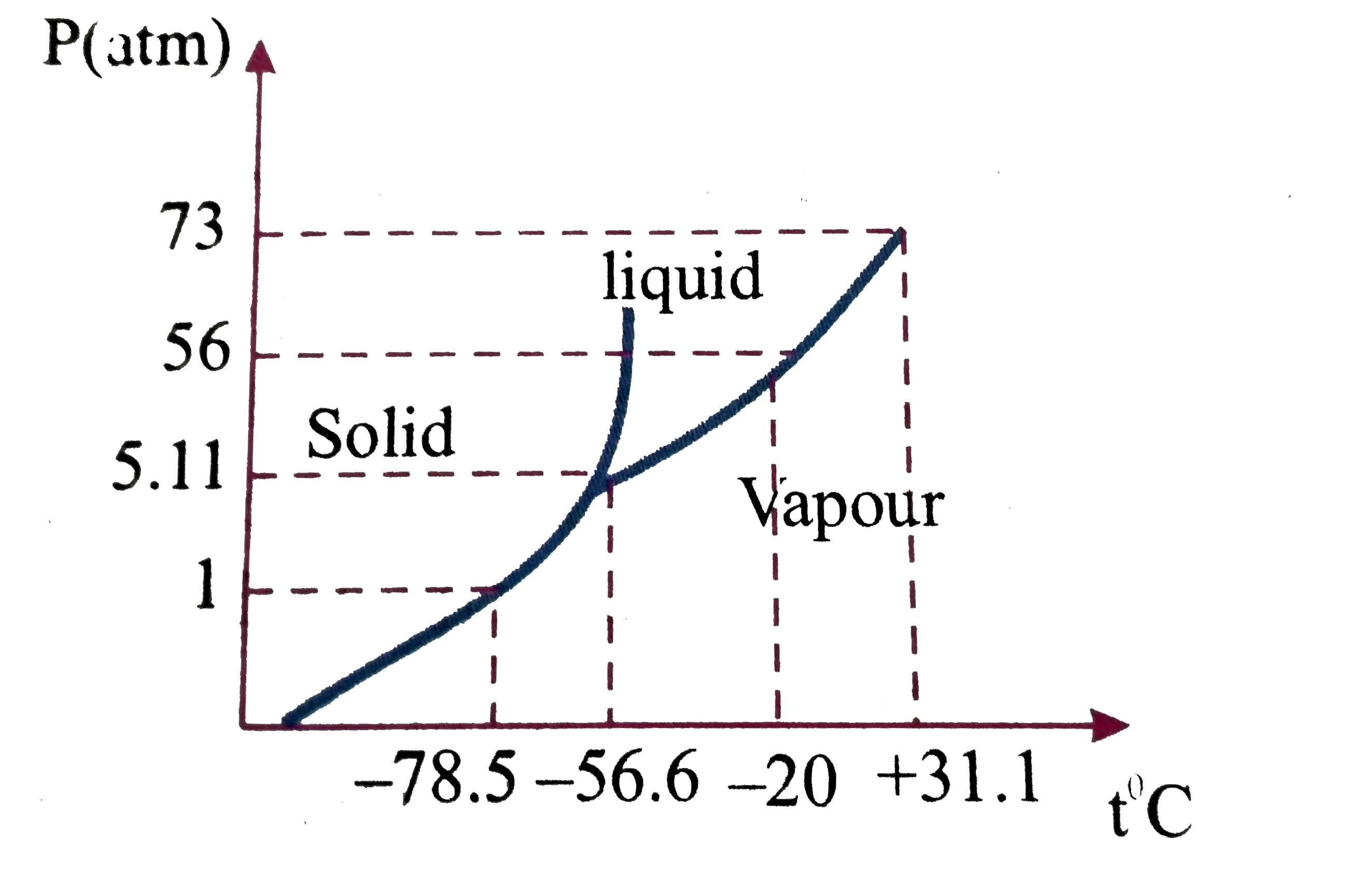 .AVapour at −79∘C under 1 atmBLiquid at −20∘C and 56 atmCsolid at −60∘C and 70 atmDCo-existing in three phase at −56.6∘C and 5.11 atm.
.AVapour at −79∘C under 1 atmBLiquid at −20∘C and 56 atmCsolid at −60∘C and 70 atmDCo-existing in three phase at −56.6∘C and 5.11 atm.In the given figure, two straight lines AB and CD intersect at a point and ∠AOC = 50∘. Then, ∠BOD = ?
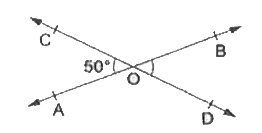 A40∘B50∘C130∘D60∘
A40∘B50∘C130∘D60∘
In the given figure, two straight lines AB and CD intersect at a point such that ∠AOC=50∘. Find: (i) ∠BOD
(ii) ∠BOC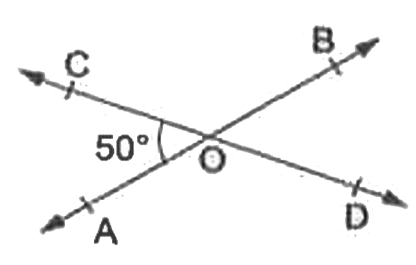
View SolutionIn the given figure , if a= b = c then ∠AOC= ______ ??
View SolutionIn the given figure, AOB is a straight line and OC is a ray such that ∠AOC=(3x+20)∘ and ∠BOC=(2x−10)∘. Find the value of x and hence find (i) ∠AOC
(ii)∠BOC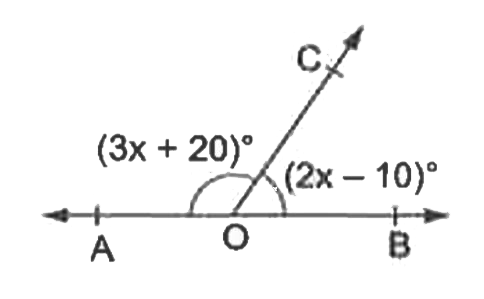
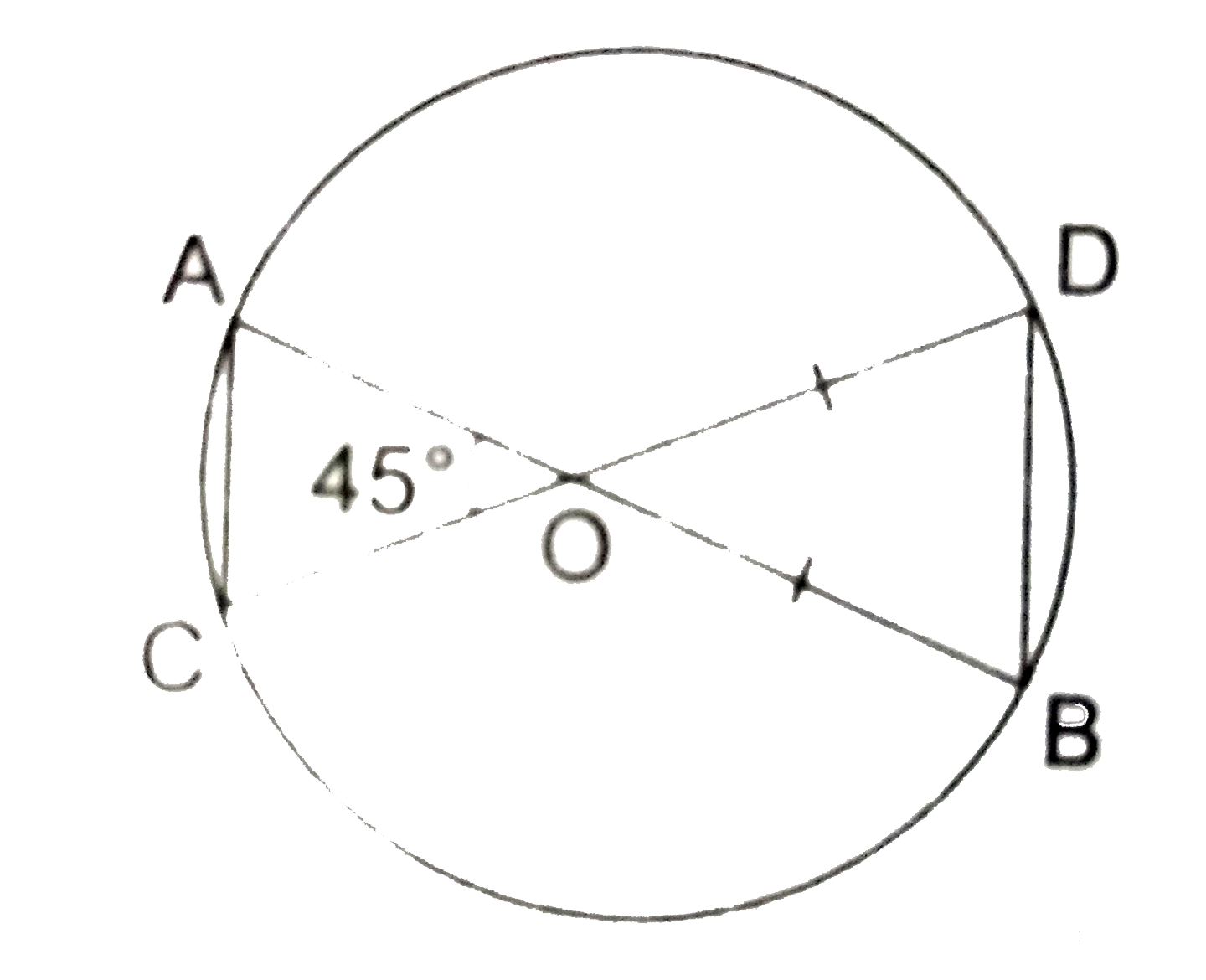
View SolutionIn the given figure, O is the point of intersection of two chords AB and CD such that OB=ODand∠AOC=45∘. Then ,ΔOACandΔODB are
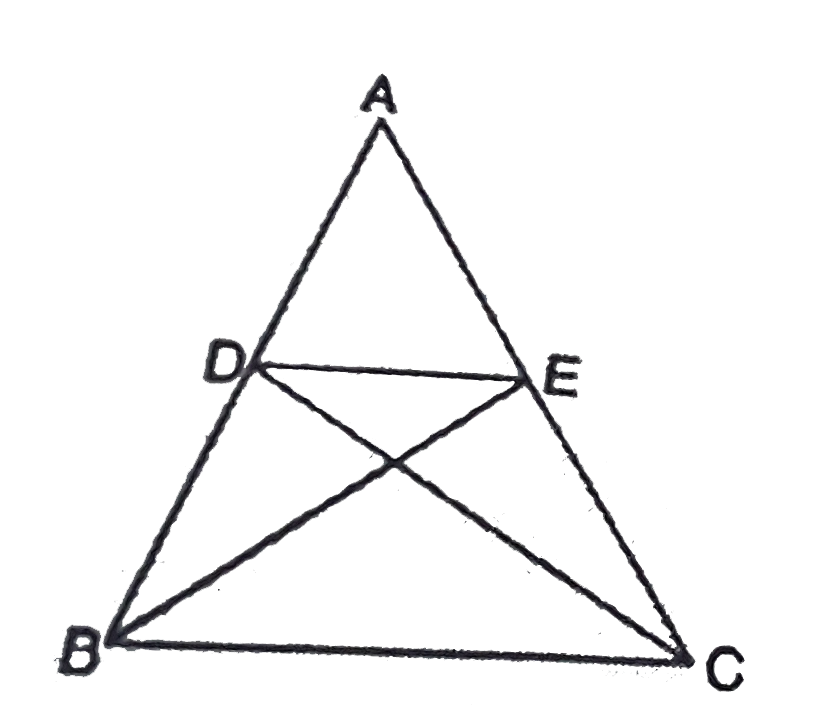
View Solutionin the given figure, if △ABE≅△ACD prove that △ADE~△ABC.
View Solution