In the given figure, O is the point of intersection of two chords AB and CD such that OB=ODand∠AOC=45∘. Then ,ΔOACandΔODB are
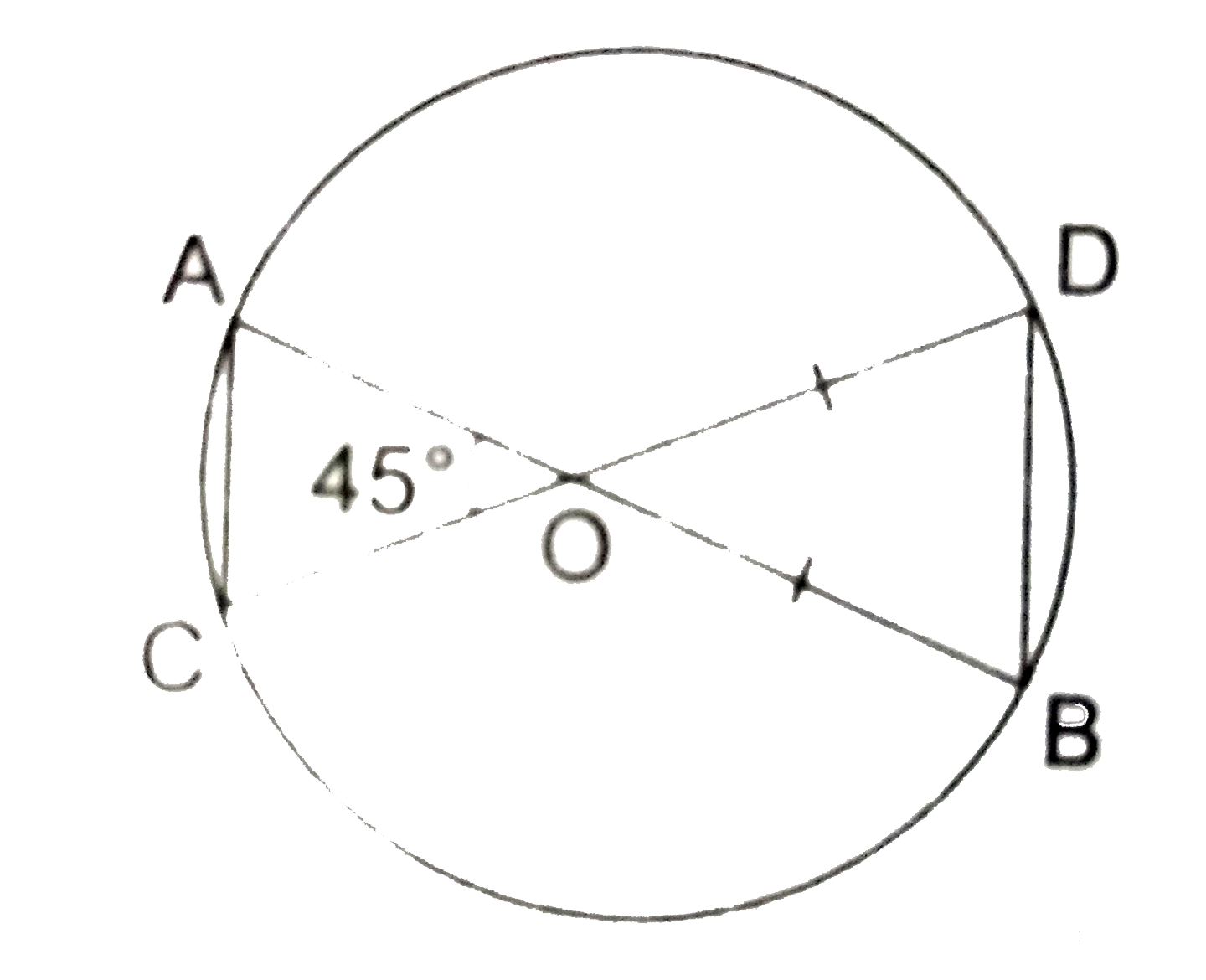
equilateral and similar
equilateral but not similar
isosceles and similar
isosceles but not similar
The correct Answer is:C
In ΔOACandΔODB, we have
∠AOC=∠DOB ( ver. Opp. ∠) and ∠OAC=∠ODB ( ∠ in the same segment)
∴ΔOAC~ΔODB→OCOB=OAOD=ACBD
∴OCOD=1⇒OC=OA[∴OB=OD (given)]
Clearly, OA≠OD.
∴OAOD≠1⇒ACBD≠⇒AC≠BD
∴ΔOACandΔODB are isosceles and similar.
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTPILE-CHOICE QUESTIONS (MCQ) ( MATCHING OF COLUMNS)
Explore 1 Video
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Test Yourself
Explore 20 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7E
Explore 30 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
In the given figure, the two lines AB and CD intersect at a point O such that ∠BOC=125∘. Find the values of x, y, and z.
View SolutionIn the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point p within the circle. If AB=15cm,PB=9cm, then find the length of PD.
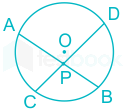
View Solution
Knowledge Check
The point of intersection of the angle bisectors of a triangle is :
AorthocentreBcentroidCincentreDcircumcentreThe point of intersection of the angle bisectors of a triangle is :
AorthocentreBcentroidCincentreDcircumcenterIn the given figure, two straight lines AB and CD intersect at a point and ∠AOC = 50∘. Then, ∠BOD = ?
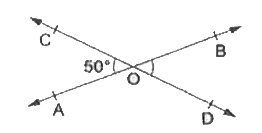 A40∘B50∘C130∘D60∘
A40∘B50∘C130∘D60∘
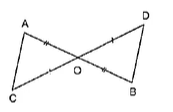
In Figure, O is the mid point of AB and CD . Prove that AOC≅BOD AC=BD (iii) ACBD
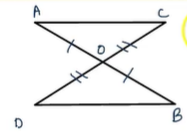
View SolutionIn the given figure, two straight lines AB and CD intersect at a point such that ∠AOC=50∘. Find: (i) ∠BOD
(ii) ∠BOC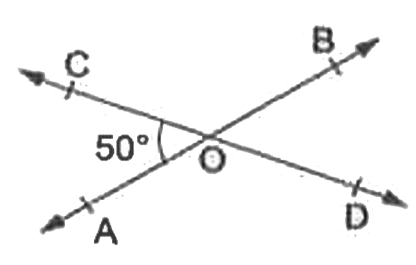
View SolutionIn Figure O is the mid-point of AB and CD. Prove that AOC≅ BOD (b) AC=BD (iii) AC∣∣BD
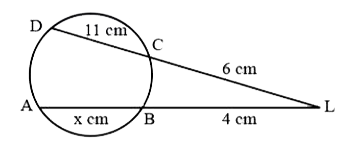
View SolutionIn the given figure, chords AB and CD are intersecting each other at point L. Find the length of AB.
View SolutionIn the figure, two chords AB and CD intersect each other at the point P.
Prove that : ΔAPC~ΔDPB

View Solution

