If ∆ABC ≅ ∆FED under the correspondence ABC ↔ FED, write all the corresponding congruent parts of the triangles
To solve the problem, we need to identify the corresponding congruent parts of the triangles ∆ABC and ∆FED, given that they are congruent (∆ABC ≅ ∆FED).
1. Identify the Correspondence:
We are given that triangle ABC corresponds to triangle FED. This means:
- A corresponds to F
- B corresponds to E
- C corresponds to D
2. Write the Corresponding Congruent Angles:
Since the triangles are congruent, their corresponding angles are also equal. Therefore:
- Angle A ≅ Angle F
- Angle B ≅ Angle E
- Angle C ≅ Angle D
3. Write the Corresponding Congruent Sides:
Similarly, the corresponding sides of the triangles are also equal. Thus, we have:
- Side AB ≅ Side FE
- Side BC ≅ Side ED
- Side AC ≅ Side FD
4. Summarize the Corresponding Parts:
We can summarize the congruent parts as follows:
- Angles:
- Angle A ≅ Angle F
- Angle B ≅ Angle E
- Angle C ≅ Angle D
- Sides:
- Side AB ≅ Side FE
- Side BC ≅ Side ED
- Side AC ≅ Side FD
Final Answer:
The corresponding congruent parts of the triangles are:
- Angles:
- Angle A ≅ Angle F
- Angle B ≅ Angle E
- Angle C ≅ Angle D
- Sides:
- Side AB ≅ Side FE
- Side BC ≅ Side ED
- Side AC ≅ Side FD
We are given that triangle ABC corresponds to triangle FED. This means:
- A corresponds to F
- B corresponds to E
- C corresponds to D
Since the triangles are congruent, their corresponding angles are also equal. Therefore:
- Angle A ≅ Angle F
- Angle B ≅ Angle E
- Angle C ≅ Angle D
Similarly, the corresponding sides of the triangles are also equal. Thus, we have:
- Side AB ≅ Side FE
- Side BC ≅ Side ED
- Side AC ≅ Side FD
We can summarize the congruent parts as follows:
- Angles:
- Angle A ≅ Angle F
- Angle B ≅ Angle E
- Angle C ≅ Angle D
- Sides:
- Side AB ≅ Side FE
- Side BC ≅ Side ED
- Side AC ≅ Side FD
The corresponding congruent parts of the triangles are:
- Angles:
- Angle A ≅ Angle F
- Angle B ≅ Angle E
- Angle C ≅ Angle D
- Sides:
- Side AB ≅ Side FE
- Side BC ≅ Side ED
- Side AC ≅ Side FD
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLESBOOK - NCERTCHAPTER - CONGRUENCE OF TRIANGLESEXERCISE - SOLVED EXAMPLES
9 Videos
- CONGRUENCE OF TRIANGLESBOOK - NCERTCHAPTER - CONGRUENCE OF TRIANGLESEXERCISE - SOLVED EXAMPLES
9 Videos
- COMPARING QUANTITIESBOOK - NCERTCHAPTER - COMPARING QUANTITIESEXERCISE - SOLVED EXAMPLES
21 Videos
- DATA HANDLINGBOOK - NCERTCHAPTER - DATA HANDLINGEXERCISE - EXERCISE 3.3
3 Videos
Similar Questions
Knowledge Check
For the given triangles, write the correspondence, if they are congruent.
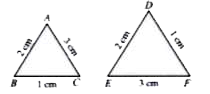 AΔABC≅ΔDEFBΔABC≅ΔEDFCΔABC≅ΔFDEDnot congruent
AΔABC≅ΔDEFBΔABC≅ΔEDFCΔABC≅ΔFDEDnot congruentIf for ΔABCandΔDEF , the correspondence CAB↔EDF gives a congruence then which of the following is not true ?
AAC = DEBAB = EFC∠A=∠DD∠B=∠FIf for ΔABC and <DEF the correspondence CAB↔EDF gives a congruence, then which of the following is not true?
AAC = DFBAB = EFC<A=<DD<B=<F
ΔABCandΔPQR are congruent under the correspondence : ABC↣RQP write the parts of ΔABC that correspond to ? (i) ¯¯¯¯¯¯PQ (ii) ∠Q (iii) ¯¯¯¯¯¯RP
View SolutionIt is necessary to write the correspondence of vertices correctly for writing congruence of triangles in symbolic form .
View SolutionWhich of the following statements are true and which of them are false?
(i) All squares are congruent.
(ii) If two squares have equal areas, they are congruent.
(iii) If two figures have equal areas, they are congruent.
(iv) If two triangles are equal in area, they are congruent.
(v) If two sides and one angle of a triangle are equal to the corresponding two sides and angle of another triangle, the triangles are congruent.
(vi) If two angles and any side of a triangle are equal to the corresponding angles and the side of another triangle then the triangles are congruent.
(vii) If three angles of a triangle are equal to the corresponding angles of another triangle then the triangles are congruent.
(viii) If the hypotenuse and an acute angle of a right triangle are equal to the hypotenuse and the corresponding acute angle of another right triangle then the triangles are congruent.
(ix) If the hypotenuse of a right triangle is equal to the hypotenuse of another right triangle then the triangles are congruent.
View Solution
Prove that for a given correspondence, if three angles of one triangles are congruent to the corresponding three angles of the other triangle, then the two triangles are similar.
View SolutionIfΔPQRandΔXYZare congruent under the correspondence QPR↔XYZ, then
∠R=…….
View Solution
