A liquid of density 900 kg/m flows through a horizontal pipe that has a cross-sectional area of 1.90×10−2m2 in region A and a cross-sectional area of 9.50×10−2m2 in region B. The pressure difference between the two regions is 720×103 Pa. What are (a) the volume flow rate and (b) the mass flow rate?
To solve the problem, we will follow these steps:
Step 1: Understand the Given Data
- Density of the liquid, ρ=900kg/m3
- Cross-sectional area at region A, AA=1.90×10−2m2
- Cross-sectional area at region B, AB=9.50×10−2m2
- Pressure difference between the two regions, ΔP=PB−PA=720×103Pa
Step 2: Apply the Equation of Continuity
The equation of continuity states that the volume flow rate must be constant throughout the pipe:
Q=AA⋅vA=AB⋅vB
From this, we can express vB in terms of vA:
vB=AAAB⋅vA
Substituting the values:
vB=1.90×10−29.50×10−2⋅vA=1.909.50⋅vA≈0.2⋅vA
Step 3: Apply Bernoulli's Equation
For a horizontal pipe, Bernoulli's equation can be simplified as:
12ρv2A+PA=12ρv2B+PB
Rearranging gives:
PB−PA=12ρ(v2A−v2B)
Substituting vB:
ΔP=12ρ(v2A−(0.2vA)2)
ΔP=12ρ(v2A−0.04v2A)=12ρ(0.96v2A)
Now substituting ΔP and ρ:
720×103=12⋅900⋅0.96v2A
720×103=432v2A
Step 4: Solve for vA
v2A=720×103432
Calculating:
v2A≈1666.67⇒vA≈√1666.67≈40.82m/s
Step 5: Calculate Volume Flow Rate Q
Using the area AA:
Q=AA⋅vA=1.90×10−2⋅40.82≈0.776m3/s
Step 6: Calculate Mass Flow Rate ˙m
Using the density:
˙m=ρ⋅Q=900⋅0.776≈698.02kg/s
Final Answers
(a) Volume Flow Rate, Q≈0.776m3/s
(b) Mass Flow Rate, ˙m≈698.02kg/s
---
- Density of the liquid, ρ=900kg/m3
- Cross-sectional area at region A, AA=1.90×10−2m2
- Cross-sectional area at region B, AB=9.50×10−2m2
- Pressure difference between the two regions, ΔP=PB−PA=720×103Pa
The equation of continuity states that the volume flow rate must be constant throughout the pipe:
Q=AA⋅vA=AB⋅vB
From this, we can express vB in terms of vA:
vB=AAAB⋅vA
Substituting the values:
vB=1.90×10−29.50×10−2⋅vA=1.909.50⋅vA≈0.2⋅vA
For a horizontal pipe, Bernoulli's equation can be simplified as:
12ρv2A+PA=12ρv2B+PB
Rearranging gives:
PB−PA=12ρ(v2A−v2B)
Substituting vB:
ΔP=12ρ(v2A−(0.2vA)2)
ΔP=12ρ(v2A−0.04v2A)=12ρ(0.96v2A)
Now substituting ΔP and ρ:
720×103=12⋅900⋅0.96v2A
720×103=432v2A
v2A=720×103432
Calculating:
v2A≈1666.67⇒vA≈√1666.67≈40.82m/s
Using the area AA:
Q=AA⋅vA=1.90×10−2⋅40.82≈0.776m3/s
Using the density:
˙m=ρ⋅Q=900⋅0.776≈698.02kg/s
(a) Volume Flow Rate, Q≈0.776m3/s
(b) Mass Flow Rate, ˙m≈698.02kg/s
Topper's Solved these Questions
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
48 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type )
10 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - CHECKPOINT
8 Videos
- ELECTROMAGNETIC WAVES BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
Ethanol of density ρ=791kg/m3 flows smoothly through a horizontal pipe that tapers (as in Fig ) in cross-sectional area from A1=1.20×10−3m2 to A2=A1/2 . The pressure difference between the wide and narrow sectional of pipe is 4120 Pa. What is the volume flow rate Rv of the ethanol ?
View SolutionA current of 4.8 A is flowing in a copper wire of cross-sectional area 3×10−4m2. Find the current density in the wire.
View Solution
Knowledge Check
A solenoid of cross-sectional area 2×10−4m2 and 900 turns has 0.6Am2 magnetic moment. Then the current flowing through it is
A2.4AB2.34mAC3.33AD3.33mAAn ideal liquid (water) flowing through a tube of non-uniform cross section area at A and B are 40cm2 and 20cm2 respectively. If pressure difference between A & B is 700 Nm2 then volume flow rate is
 A2732 cm3sB2142 cm3sC1832 cm3sD3218 cm3s
A2732 cm3sB2142 cm3sC1832 cm3sD3218 cm3s
Water flowing steadily through a horizontal pipe of non-unifrom cross-section. If the pressure of water is 4×104N/m2 at a point where cross-section is 0.02m2 and velocity of flow is 2ms−1 . The pressure at a point where cross-section reduces to 0.01m2 is 3.4×10n Pa. What is the value of n ?
View SolutionIf 106 electrons/s are flowing through an area of cross section of 10−4m2 then the current will be:-
View SolutionWater is moving with a speed of 5.0 m/s through a pipe with a cross-sectional area of 4.0cm2. The water gradually descends 12 m as the pipe cross-sectional area increases to 8.0cm2 (a) What is the speed at the lower level? (b) If the pressure at the upper level is 1.5×105 Pa, what is the pressure at the lower level?
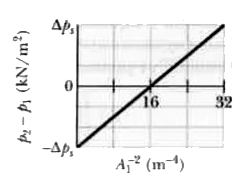
View SolutionFresh water flows horizontally from pipe section 1 of cross-sectional area A, into pipe section 2 of cross-sectional area A2 Figure gives a plot of the pressure difference p2−p1 versus the inverse area squared A−21 that would be expected for a volume flow rate of a certain value if the water flow were laminar under all circumstances. The scale on the vertical axis is set by Δps=600kN/m2. For the conditions of the figure, what are the values of (a) A2 and (b) the volume flow rate?
View SolutionWhat is the drift velocity of electrons in a copper conductor having a cross-sectional area of 5×10−6m2 if the current is 10 A. Assume there are 8.0×1028electrons/m3.
View SolutionWater is flowing with a speed of 2m/s in a horizontal pipe with cross-sectional area decreasing from 2×10−2m2 to 0.01m2 at pressure 4×104 pascal. What will be the pressure at smaller cross-section?
View Solution
