What gauge pressure must a machine produce in order to suck mud of density 1800 kg/m3 up a tube by a height of 2.0 m?
To solve the problem of determining the gauge pressure required to suck mud with a density of 1800 kg/m³ up a tube by a height of 2.0 m, we can follow these steps:
1. Understand the Concept of Gauge Pressure:
Gauge pressure is the pressure relative to atmospheric pressure. When sucking a fluid (in this case, mud) up a tube, the pressure at the bottom of the tube must be greater than the pressure at the top by an amount sufficient to lift the fluid.
2. Identify the Relevant Variables:
- Density of mud (ρ) = 1800 kg/m³
- Height (h) = 2.0 m
- Acceleration due to gravity (g) = 9.81 m/s²
3. Use the Hydrostatic Pressure Formula:
The pressure difference (ΔP) required to lift the mud can be calculated using the formula:
ΔP=ρ⋅g⋅h
where:
- ΔP is the pressure difference,
- ρ is the density of the fluid,
- g is the acceleration due to gravity,
- h is the height the fluid is lifted.
4. Substitute the Values into the Formula:
ΔP=1800kg/m3×9.81m/s2×2.0m
5. Calculate the Pressure Difference:
ΔP=1800×9.81×2.0
ΔP=1800×19.62
ΔP=35316Pa
6. Convert to Gauge Pressure:
Since gauge pressure is the pressure relative to atmospheric pressure, the required gauge pressure to suck the mud up is:
Pgauge=ΔP=35316Pa≈3.53×104Pa
Final Answer:
The gauge pressure that the machine must produce in order to suck mud of density 1800 kg/m³ up a tube by a height of 2.0 m is approximately 3.53×104Pa.
---
Gauge pressure is the pressure relative to atmospheric pressure. When sucking a fluid (in this case, mud) up a tube, the pressure at the bottom of the tube must be greater than the pressure at the top by an amount sufficient to lift the fluid.
- Density of mud (ρ) = 1800 kg/m³
- Height (h) = 2.0 m
- Acceleration due to gravity (g) = 9.81 m/s²
The pressure difference (ΔP) required to lift the mud can be calculated using the formula:
ΔP=ρ⋅g⋅h
where:
- ΔP is the pressure difference,
- ρ is the density of the fluid,
- g is the acceleration due to gravity,
- h is the height the fluid is lifted.
ΔP=1800kg/m3×9.81m/s2×2.0m
ΔP=1800×9.81×2.0
ΔP=1800×19.62
ΔP=35316Pa
Since gauge pressure is the pressure relative to atmospheric pressure, the required gauge pressure to suck the mud up is:
Pgauge=ΔP=35316Pa≈3.53×104Pa
The gauge pressure that the machine must produce in order to suck mud of density 1800 kg/m³ up a tube by a height of 2.0 m is approximately 3.53×104Pa.
Topper's Solved these Questions
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
48 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type )
10 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - CHECKPOINT
8 Videos
- ELECTROMAGNETIC WAVES BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
If you can produce a minimum gauge pressure of −2.5×10−3 atm in your lungs, to what maximum height can you suck tea (density 1000 kg/m3 ) up a straw?
View SolutionA solid of density 5000kgm3 weghs 0.5 kg f in air. It is completely immersed in water of density 1000kgm3.
(a) Calculate the apparent weight of the solid in water.
(b) what will be its apparent weight if water is replaced by a liquid of density 8000 kgm3?
View Solution
Knowledge Check
Barometer is constructed using liquid . What would be height of liquid column when mercury barometer reads 76cm
A13.6mB136mC0.76mD1.36mWhat is the height of air column which will produce a pressure of 1 atm? Density of air is 1.3 kg/m3.
A6.45 kmB7.20 kmC7.95 kmD8.40 kmWhat is the velocity of wave in monatomic gas having pressure 1 kilo pascal and density 2.6 kg/m3
A8.9×103m/sB3.6m/sCZeroDNone of these .
Find the total pressure inside a sperical air bubble of radius 0.2 mm. The bubble is at a depth 5 cm below the surface of a liquid of density 2×103 kg m−3 and surface tension 0.082 N m−1. (Given : atmospheric pressure = 1.01 ×105Nm−2)
Hint : Pi=Po+2SR
Po = atmospheric pressure + gauge pressure of liquid column.
View SolutionTo what height does the liquid rise in a capillary tube of radus 0.25 mm, when dipped in a liquid of density 0.8×103kgm−3 and surface tension 0.05 N m−1? Given (cosθ=0.4)
View Solutionan open - ended U-tube cross - sectional area contains water (density 103Kg m−3). Initially the water level stands at 0.29 m from the bottom in each arm. Kerosene oil (a wtare - immiscible liquid) of density 800 kg m−3 is added to the left arm until its length is 0.1 m, as shown in the schematic figure below. The ratio (h1h2) of the heights of the liquid in the two arms is
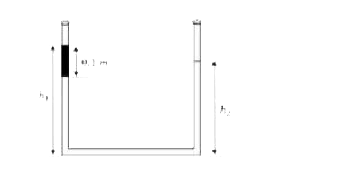
View SolutionA cube of ice of side length 10 cm is floating in water of density 1000 kg/m3. Then pick up the correct statement (density of ice = 900 kg/m3)
View SolutionFor air at room temperature the atmospheric pressure is 1.0×105Nm−2 and density of air is 1.2 kgm−3. For a tube of length 1.0 m closed at one end the lowest frequency generated is 84 Hz. The value of y (ratio of two specific heats) for air is
View Solution
