A flotation device is in the shape of a right cylinder, with a height of 0.650 m and a face area of 4.00m2 on top and bottom, and its density is 0.300 times that of fresh water. It is initially held fully submerged in fresh water, with its top face at the water surface. Then it is allowed to ascend gradually until it begins to float. How much work does the buoyant force do on the device during the ascent?
To solve the problem, we need to calculate the work done by the buoyant force on the flotation device as it ascends from being fully submerged to the point where it begins to float. Here’s a step-by-step breakdown of the solution:
Step 1: Calculate the volume of the flotation device
The volume V of a cylinder is given by the formula:
V=A×h
where A is the face area and h is the height of the cylinder.
Given:
- A=4.00m2
- h=0.650m
Calculating the volume:
V=4.00m2×0.650m=2.60m3
Step 2: Calculate the weight of the flotation device
The weight W of the flotation device can be calculated using the formula:
W=density×V×g
where g is the acceleration due to gravity (approximately 9.81m/s2).
The density of fresh water is 1000kg/m3, and the density of the flotation device is 0.300×1000kg/m3=300kg/m3.
Calculating the weight:
W=300kg/m3×2.60m3×9.81m/s2=7843.8N
Step 3: Calculate the buoyant force acting on the flotation device
The buoyant force Fb is equal to the weight of the water displaced by the flotation device. This can be calculated as:
Fb=density of water×V×g
Using the density of fresh water:
Fb=1000kg/m3×2.60m3×9.81m/s2=25506N
Step 4: Determine the net force acting on the flotation device
The net force Fnet acting on the flotation device as it ascends is given by:
Fnet=Fb−W
Calculating the net force:
Fnet=25506N−7843.8N=17662.2N
Step 5: Calculate the distance the flotation device ascends
The flotation device will ascend until the buoyant force equals its weight. At this point, it will float. The height hf at which it begins to float can be calculated using the relationship:
Fb=W
Let hf be the height of the submerged part of the device when it starts to float. The volume of water displaced at this height is:
Vf=A×hf
Setting the buoyant force equal to the weight:
1000kg/m3×Vf×g=W
Substituting for Vf:
1000kg/m3×(4.00m2×hf)×9.81m/s2=7843.8N
Solving for hf:
hf=7843.81000×4.00×9.81=0.200m
Step 6: Calculate the work done by the buoyant force
The work done Wb by the buoyant force during the ascent is given by:
Wb=Fb×hf
Calculating the work done:
Wb=25506N×0.200m=5101.2J
Final Answer
The work done by the buoyant force on the device during the ascent is approximately 5101.2J.
---
The volume V of a cylinder is given by the formula:
V=A×h
where A is the face area and h is the height of the cylinder.
- A=4.00m2
- h=0.650m
V=4.00m2×0.650m=2.60m3
The weight W of the flotation device can be calculated using the formula:
W=density×V×g
where g is the acceleration due to gravity (approximately 9.81m/s2).
W=300kg/m3×2.60m3×9.81m/s2=7843.8N
The buoyant force Fb is equal to the weight of the water displaced by the flotation device. This can be calculated as:
Fb=density of water×V×g
Using the density of fresh water:
Fb=1000kg/m3×2.60m3×9.81m/s2=25506N
The net force Fnet acting on the flotation device as it ascends is given by:
Fnet=Fb−W
Calculating the net force:
Fnet=25506N−7843.8N=17662.2N
The flotation device will ascend until the buoyant force equals its weight. At this point, it will float. The height hf at which it begins to float can be calculated using the relationship:
Fb=W
Let hf be the height of the submerged part of the device when it starts to float. The volume of water displaced at this height is:
Vf=A×hf
Setting the buoyant force equal to the weight:
1000kg/m3×Vf×g=W
Substituting for Vf:
1000kg/m3×(4.00m2×hf)×9.81m/s2=7843.8N
Solving for hf:
hf=7843.81000×4.00×9.81=0.200m
The work done Wb by the buoyant force during the ascent is given by:
Wb=Fb×hf
Calculating the work done:
Wb=25506N×0.200m=5101.2J
The work done by the buoyant force on the device during the ascent is approximately 5101.2J.
Topper's Solved these Questions
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
48 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type )
10 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - CHECKPOINT
8 Videos
- ELECTROMAGNETIC WAVES BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
Figure shows a vertical wall of horizontal length L = 5.0 m and depth H = 3.0 m that is fully submerged in water , with its top surface of the water . What is the force on the wall due to the water pressure ?

View SolutionSalt water is slightly dense than fresh water. Will a boat float higher in salt water on in fresh water?
View Solution
Knowledge Check
The radius of the base of a right cylinder is 14m and its height is 21m. Its total surface area is :
A1848m2B1848 m3C3080dm2D3080 m2A reservoir is in the shape of a frustum of a right circular cone. It is 8 m across at the top and 4 m across at the bottom. If it is 6 m deep, then its capacity is 176 m3 (b) 196 m3 (c) 200 m3 (d) 110 m3
A224m3B176m3C225m3Dnone of theseHow much percentage of fresh water is available on Earth?
A3%B37%C3.7%D2.7%
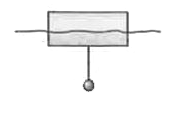
Figure shows an iron ball suspended by thread of negligible mass from an upright cylinder that floats partially submerged in water. The cylinder has a height of 6.00 cm, a face area of 12.0cm2 on the top and bottom, and a density of 0.25g/cm2 , and 1.00 cm of its height is above the water surface. What is the radius of the iron ball?
View SolutionIf a fresh egg is put into a beaker filled with water, it sinks On dissolving a lot of salt in the water, the egg begins to rise and then floats. Why ?
View SolutionWater fall from height 63m. Find temperature difference of water between top and bottom position.
View SolutionAn inflatable device with a density of 1.20 g/cm3 is fully submerged in fresh water and then inflated enough for the device's density to match that of the water. What then is the ratio of the expanded volume to the full volume of the device?
View SolutionA tank filled with fresh water has a hole in its bottom and water is flowing out of it. If the size of the hole is increased, then
View Solution
