A large aquarium of height 5.00 m is filled with fresh water to a depth of 2.00 m. One wall of the aquarium consists of thick plastic 9.00 m wide. By how much does the total force on that wall increase if the aquarium is next filled to a depth of 4.00 m?
To solve the problem, we need to calculate the increase in the total force on the wall of the aquarium when the water level rises from 2.00 m to 4.00 m. The force exerted by the water on the wall can be calculated using the hydrostatic pressure formula.
1. Understand the Problem:
- The aquarium has a height of 5.00 m and is initially filled with water to a depth of 2.00 m.
- The width of the wall is 9.00 m.
- We need to find the increase in force when the water level is raised to 4.00 m.
2. Calculate the Initial Force (F1) at 2.00 m:
- The pressure at a depth h is given by P=ρgh, where:
- ρ (density of water) = 1000 kg/m³,
- g (acceleration due to gravity) = 9.81 m/s²,
- h1=2.00 m (initial depth).
- The force on the wall is given by the formula:
F1=12ρgh21×L
- Substituting the values:
F1=12×1000×9.81×(2.00)2×9.00
- Calculating F1:
F1=12×1000×9.81×4×9=176580N
3. Calculate the Final Force (F2) at 4.00 m:
- Now, we calculate the force when the water level is at 4.00 m:
- Using the same formula:
F2=12ρgh22×L
- Where h2=4.00 m:
F2=12×1000×9.81×(4.00)2×9.00
- Calculating F2:
F2=12×1000×9.81×16×9=705840N
4. Calculate the Increase in Force (ΔF):
- The increase in force is given by:
ΔF=F2−F1
- Substituting the values:
ΔF=705840−176580=529260N
5. Final Answer:
- The total force on the wall increases by 529260 N when the aquarium is filled to a depth of 4.00 m.
- The aquarium has a height of 5.00 m and is initially filled with water to a depth of 2.00 m.
- The width of the wall is 9.00 m.
- We need to find the increase in force when the water level is raised to 4.00 m.
- The pressure at a depth h is given by P=ρgh, where:
- ρ (density of water) = 1000 kg/m³,
- g (acceleration due to gravity) = 9.81 m/s²,
- h1=2.00 m (initial depth).
- The force on the wall is given by the formula:
F1=12ρgh21×L
- Substituting the values:
F1=12×1000×9.81×(2.00)2×9.00
- Calculating F1:
F1=12×1000×9.81×4×9=176580N
- Now, we calculate the force when the water level is at 4.00 m:
- Using the same formula:
F2=12ρgh22×L
- Where h2=4.00 m:
F2=12×1000×9.81×(4.00)2×9.00
- Calculating F2:
F2=12×1000×9.81×16×9=705840N
- The increase in force is given by:
ΔF=F2−F1
- Substituting the values:
ΔF=705840−176580=529260N
- The total force on the wall increases by 529260 N when the aquarium is filled to a depth of 4.00 m.
Topper's Solved these Questions
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
48 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type )
10 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - CHECKPOINT
8 Videos
- ELECTROMAGNETIC WAVES BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
Light of wavelength 560 nm goes through a pinhole of diameter 0.20 mm and falls on a wall at a distance of 2.00 m. What will be the radius of the central bright spot formed on the wall ?
View SolutionThe plastic tube in Fig. has a cross-sectional area of 5.00 cm2. The tube is filled with water until the short arm (of length d = 0.800 m) is full. Then the short arm is figure sealed and more water is gradually poured into the long arm. When the total height of water in the long arm reaches 2.80 m, the seal is on the verging of popping. What force is then on the seal?
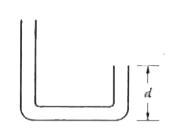
View Solution
Knowledge Check
A swimming pool has the dimensions shown in the figure . It is filled with water to a uniform depth of 8.00 m . The density of water = 1.00×103kg/m3
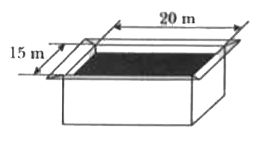
What is the total force exerted on the bottom of the swimming pool ?A2.40×107NB5.90×107NC5.40×107ND7.50×107 NThe side of glass aquarium is 1 m high and 2m long, when the aquarium is filled to the top with water what is the total force against the side-
A980×103NB9.8×103NC0.98×103ND0.098×103NA swimming pool has the dimensions shown in the figure . It is filled with water to a uniform depth of 8.00 m . The density of water = 1.00×103kg/m3
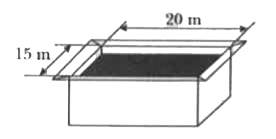
What is the total pressure exerted on the bottom of the swimming pool ?A0.79×105 PaB1.80×105 PaC1.48×105 PaD1.97×105 Pa
A horizontal force of magnitude 41.0 N pushes a block of mass 4.00 kg across a floor where the coefficient of kinetic friction is 0.600. (a) How much work is done by that applied force on the block-floor system when the block slides through a displacement of 2.00 m across the floor ? (b) During that displacement, the thermal energy of the block increases by 40.0 J. What is the increase in thermal energy of the floor ? (c) What is the increase in the kinetic energy of the block ?
View SolutionHow much volume of 10MHCI should be diluted with water to prepare 2.00L of 5MHCI?
View SolutionHow much volume of 10MHCI should be diluted with water to prepare 2.00L of 5MHCI?
View SolutionA tank with vertical walls is monted so that its base is at height of 1.2 m above the horizotnal ground. The tank is filled with water to depth 2.8 m. A holw is punched in the side wall of the tank at a depth x m below the surface of water to have maximum range of the emerging stream. then the value of x in metre is
View SolutionA parallel plate capacitor of plate area 2.00×10−2m2 is filled with two dielectric slabs, each with thickness 2.00mm. One slab has dielectric consant 3.00, and the other,4.00 as shown in the figure.

How much charge does the capacitor store when charged by a 7.00 battery?
View Solution
