Ethanol of density ρ=791kg/m3 flows smoothly through a horizontal pipe that tapers (as in Fig ) in cross-sectional area from A1=1.20×10−3m2 to A2=A1/2 . The pressure difference between the wide and narrow sectional of pipe is 4120 Pa. What is the volume flow rate Rv of the ethanol ?
To solve the problem of finding the volume flow rate Rv of ethanol flowing through a tapering pipe, we can follow these steps:
Step 1: Identify Given Data
- Density of ethanol, ρ=791kg/m3
- Cross-sectional area at the wider section, A1=1.20×10−3m2
- Cross-sectional area at the narrower section, A2=A12=1.20×10−32=0.60×10−3m2
- Pressure difference, P1−P2=4120Pa
Step 2: Apply the Continuity Equation
According to the continuity equation, the flow rate must be constant throughout the pipe:
A1V1=A2V2
From this, we can express V2 in terms of V1:
V2=A1A2V1=A1A12V1=2V1
Step 3: Apply Bernoulli's Equation
Using Bernoulli's equation between points 1 and 2:
P1+12ρV21=P2+12ρV22
Rearranging gives:
P1−P2=12ρ(V22−V21)
Substituting V2=2V1:
P1−P2=12ρ((2V1)2−V21)=12ρ(4V21−V21)=12ρ(3V21)
Thus:
4120=12⋅791⋅3V21
Step 4: Solve for V1
Rearranging the equation:
4120=23672V21
V21=4120⋅22367=82402367≈3.48
Taking the square root:
V1≈√3.48≈1.86m/s
Step 5: Calculate Volume Flow Rate Rv
Using the formula for volume flow rate:
Rv=A1V1
Substituting the values:
Rv=1.20×10−3×1.86≈2.23×10−3m3/s
Final Answer
The volume flow rate Rv of the ethanol is approximately:
Rv≈2.23×10−3m3/s
- Density of ethanol, ρ=791kg/m3
- Cross-sectional area at the wider section, A1=1.20×10−3m2
- Cross-sectional area at the narrower section, A2=A12=1.20×10−32=0.60×10−3m2
- Pressure difference, P1−P2=4120Pa
According to the continuity equation, the flow rate must be constant throughout the pipe:
A1V1=A2V2
From this, we can express V2 in terms of V1:
V2=A1A2V1=A1A12V1=2V1
Using Bernoulli's equation between points 1 and 2:
P1+12ρV21=P2+12ρV22
Rearranging gives:
P1−P2=12ρ(V22−V21)
Substituting V2=2V1:
P1−P2=12ρ((2V1)2−V21)=12ρ(4V21−V21)=12ρ(3V21)
Thus:
4120=12⋅791⋅3V21
Rearranging the equation:
4120=23672V21
V21=4120⋅22367=82402367≈3.48
Taking the square root:
V1≈√3.48≈1.86m/s
Using the formula for volume flow rate:
Rv=A1V1
Substituting the values:
Rv=1.20×10−3×1.86≈2.23×10−3m3/s
The volume flow rate Rv of the ethanol is approximately:
Rv≈2.23×10−3m3/s
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.191videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.201videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.171videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELECTROMAGNETIC WAVES
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
Similar Questions
A liquid of density 900 kg/m flows through a horizontal pipe that has a cross-sectional area of 1.90×10−2m2 in region A and a cross-sectional area of 9.50×10−2m2 in region B. The pressure difference between the two regions is 720×103 Pa. What are (a) the volume flow rate and (b) the mass flow rate?
View SolutionWater is flowing with a speed of 2m/s in a horizontal pipe with cross-sectional area decreasing from 2×10−2m2 to 0.01m2 at pressure 4×104 pascal. What will be the pressure at smaller cross-section?
View Solution
Knowledge Check
- Question 1 - Select One
A fluid of density ρ flows through a horizontal pipe having two different cross-section s of areas A and 2A, Th e pressure at the smaller cross-section is P and lluid velocity at that section is v· What is the velocity and pressure at the larger cross-sect ion
Av2,P+12ρv2Bv4,P+38ρv2Cv2,P+38ρv2Dv,P+34ρv2 - Question 2 - Select One or More
A liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then
 Athe volume of the liquid flowing through the tube in unit time is A1v1Bv2−v1=√2ghCv22−v21=2ghDthe energy per unit mass of the liquid is the same in both sections of the tube
Athe volume of the liquid flowing through the tube in unit time is A1v1Bv2−v1=√2ghCv22−v21=2ghDthe energy per unit mass of the liquid is the same in both sections of the tube - Question 3 - Select One
Water is flowing steadily through a horizontal pipe of non - uniform cross - section . If the velocity of water cross - section is 0.02m2 is 2m/s , what is the velocity of water at another point where the cross - section is 0.01m2 ?
A1 m/sB2 m/sC3 m/sD4 m/s
(i) Air (density=ρ) flows through a horizontal venturi tube that discharges to the atmosphere. The area of cross section of the tube is A1 and at the constriction it is A2. The constriction is connected to a water (density=ρ0) tank through a vertical pipe of lenght H. Find the volume flow rate (Q) of the air through tube that is needed to just draw the water into the tube.
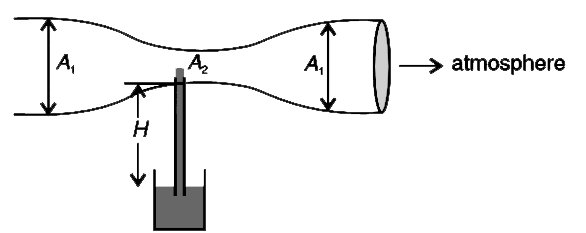
(ii) A non viscous liquid of constant density ρ flows in a stremline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in the figure. The area of cross section of the tube at two points P and Q at heights of h1 and h2 are respectively A1 and A2. The velocity of the liquid at point P is v. Find the work done on a small volume ΔV of fluid by the neighbouring fluid as the small volume moves from P to Q.
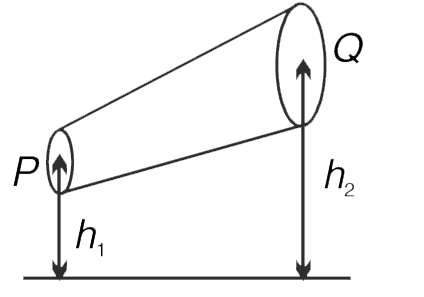 View Solution
View SolutionWater at a pressure of 4×104Nm−2 flows at 2ms−1 through a horizontal pope of 0.02m2. What is the pressure in the smaller cross-section of the pipe?
View SolutionWater flowing steadily through a horizontal pipe of non-unifrom cross-section. If the pressure of water is 4×104N/m2 at a point where cross-section is 0.02m2 and velocity of flow is 2ms−1 . The pressure at a point where cross-section reduces to 0.01m2 is 3.4×10n Pa. What is the value of n ?
View SolutionWater flow through a horizontal pipe. The area of cross-second at one place A1=10cm2, velocity of water flow is 1ms−1 and pressure is 2000 Pa. At another place area A2=5cm2. Whate is the pressure at area A2 ?
View SolutionA liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h, then
 View Solution
View Solution
