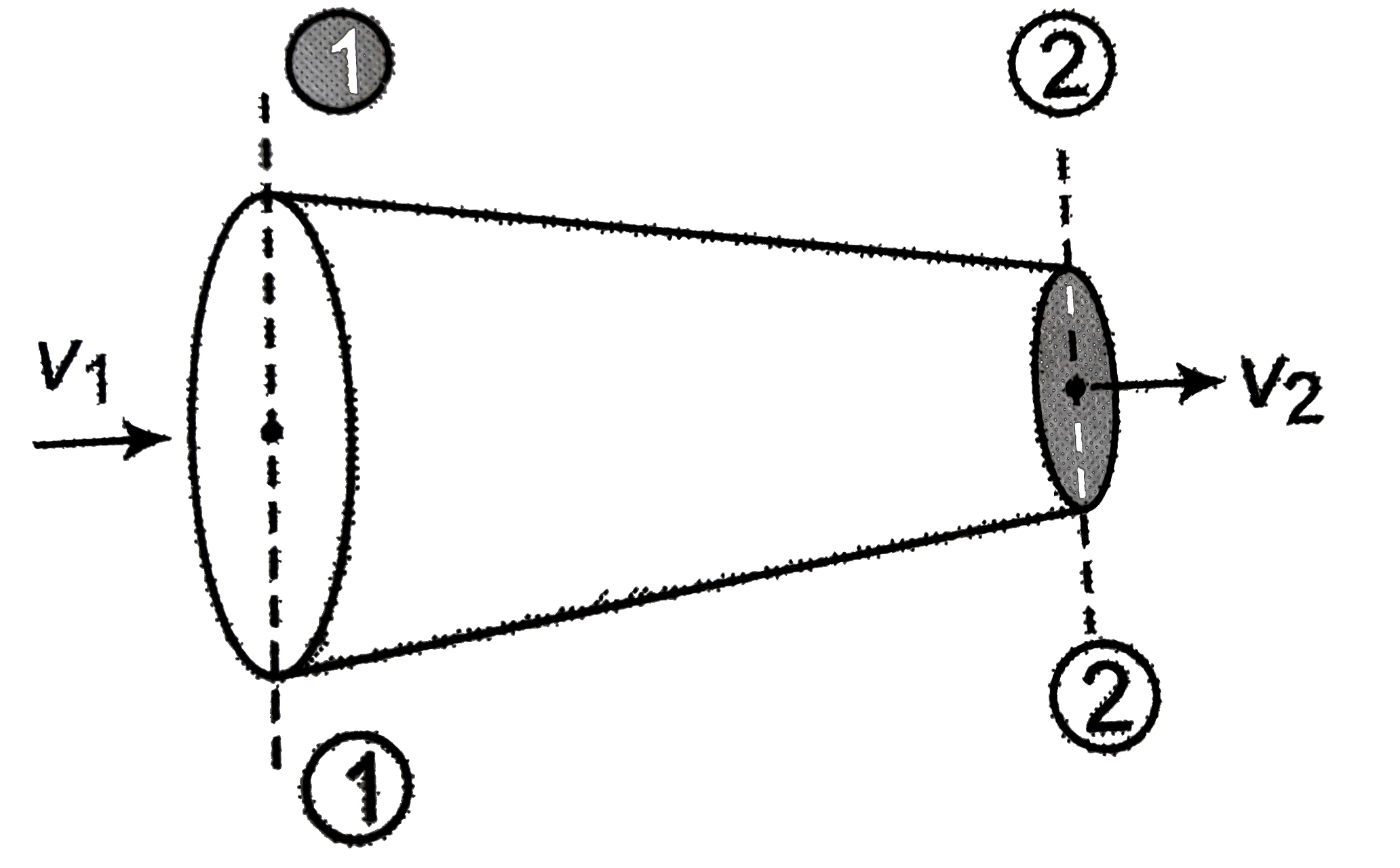
A fluid of density rho flows through a horizontal pipe having two diff

Water is flowing steadily through a horizontal pipe of non-uniform cross-section. If the pressure of water is $4 \times 10^{4} N / m^{2}$ at a point where cross-section is $0.02 m^{2}$ and velocity of flow is $2 m / s$ . What is the pressure at a point where cross-section reduces to $0.01 m^{2}$ ?
.
A $1.4 \times 10^{4} N / m^{2}$
B $3.4 \times 10^{4} N / m^{2}$
C $2.4 \times 10^{- 4} N / m^{2}$
Dnone of these
A liquid is under stream lined motion through a horizontal pipe of non uniform cross section. If the volume rate of flow at cross section $a$ is V, the volume rate of flow at cross section $\frac{a}{2}$ is
A $\frac{V}{2}$
B $2 V$
C $\frac{V}{4}$
D $V$
Water is flowing steadily through a horizontal pipe of non - uniform cross - section . If the velocity of water cross - section is $0.02 m^{2}$ is 2m/s , what is the velocity of water at another point where the cross - section is $0.01 m^{2}$ ?
A1 m/s
B2 m/s
C3 m/s
D4 m/s

A fluid of density $ρ$ flows through a horizontal pipe having two different cross-section s of areas A and 2A, Th e pressure at the smaller cross-section is P and lluid velocity at that section is v· What is the velocity and pressure at the larger cross-sect ion