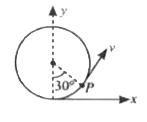
A particle of specific charge $\frac{q}{m} = π C k g^{- 1}$ is projected from the origin toward positive x-axis with a velocity of $10 m s^{- 1}$ in a uniform magnetic field $\to B = - 2 ˆ k T .$ The velocity $\to v$ of particle after time $t = \frac{1}{12} s$ will be (in $m s^{- 1}$ )

$5 [ˆ i + \sqrt{3} ˆ j]$

$5 [\sqrt{3} ˆ i - ˆ j]$

$5 [3 ˆ i + ˆ j]$

$5 [ˆ i + ˆ j]$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

A particle of specific charge $q / m = (π) C / k g$ is projected from the origin towards positive x-axis with a velocity of $10 m / s$ in a uniform magnetic field $\to B = - 2 ˆ K$ Tesla. The velocity $\to V$ of the particle after time $t = 1 / 6$ s will be
A $(5 ˆ i + 5 \sqrt{3} ˆ j) m / s$
B $10 ˆ j m / s$
C $(5 \sqrt{3} ˆ i + 5 ˆ j) m / s$
D $- 10 ˆ j m / s$
A particle of specific charge $\frac{q}{m} = π C / k g$ is projected from the origin towards positive $x$ -axis with a velocity of $10 m / s$ in a uniform magnetic field $\to B = - 2 ˆ k T$ . The velocity $\to v$ of particle after time $t = \frac{1}{12} s$ will be (in $m / s$ )
A $5 [ˆ i + \sqrt{3} ˆ j]$
B $5 [\sqrt{3} ˆ i + ˆ j]$
C $5 [\sqrt{3} ˆ i - ˆ j]$
D $5 [ˆ i + ˆ j]$
A charged particle of specific charge (charge/mass) $α$ released from origin at time $t = 0$ with velocity $\to v = v_{0} (ˆ i + ˆ j)$ in uniform magnetic field $\to B = B_{0} ˆ i .$ Coordinates of the particle at time $t = π / (B_{0} α)$ are
A $(\frac{v_{0}}{2 B_{0} α}, \frac{\sqrt{2} v_{0}}{α B_{0}}, \frac{- v_{0}}{B_{0} α})$
B $(\frac{v_{0}}{2 B_{0} α}, 0, 0)$
C $(0, \frac{2 v_{0}}{B_{0} α}, \frac{v_{0} π}{2 B_{0} α})$
D $(\frac{v_{0} π}{B_{0} α}, 0, \frac{- 2 v_{0}}{B_{0} α})$