A long conducting wire carrying a current I is bent at 120∘( see figure). The magnetic field B at a point P on the right bisector of bending angle at a distance d from the bend is
(μ0 is the permeability of free space)

3μ0I2πd
μ0I2πd
μ0I√3πd
√3μ0I2πd
The correct Answer is:D
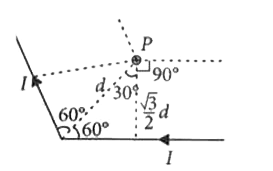
Magnetic field at P due to current through the bent wire is B=2⎡⎢
⎢⎣μ04πI(√32d)(sin90∘+sin30∘)⎤⎥
⎥⎦=2⎡⎢
⎢⎣μ04πI(√32d)(1+12)⎤⎥
⎥⎦=√3μ0I2πd
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENTBook:MTG-WBJEEChapter:MAGNETIC EFFECT OF CURRENTExercise:WB JEE Previous Years Questions
Explore 22 Videos
- LAWS OF MOTION Book:MTG-WBJEEChapter:LAWS OF MOTION Exercise:WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
Explore 2 Videos
- MAGNETICSBook:MTG-WBJEEChapter:MAGNETICSExercise:WB JEE Previous Years Questions (Category 3: One or More than one Option)
Explore 2 Videos
Similar Questions
Knowledge Check
A long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.
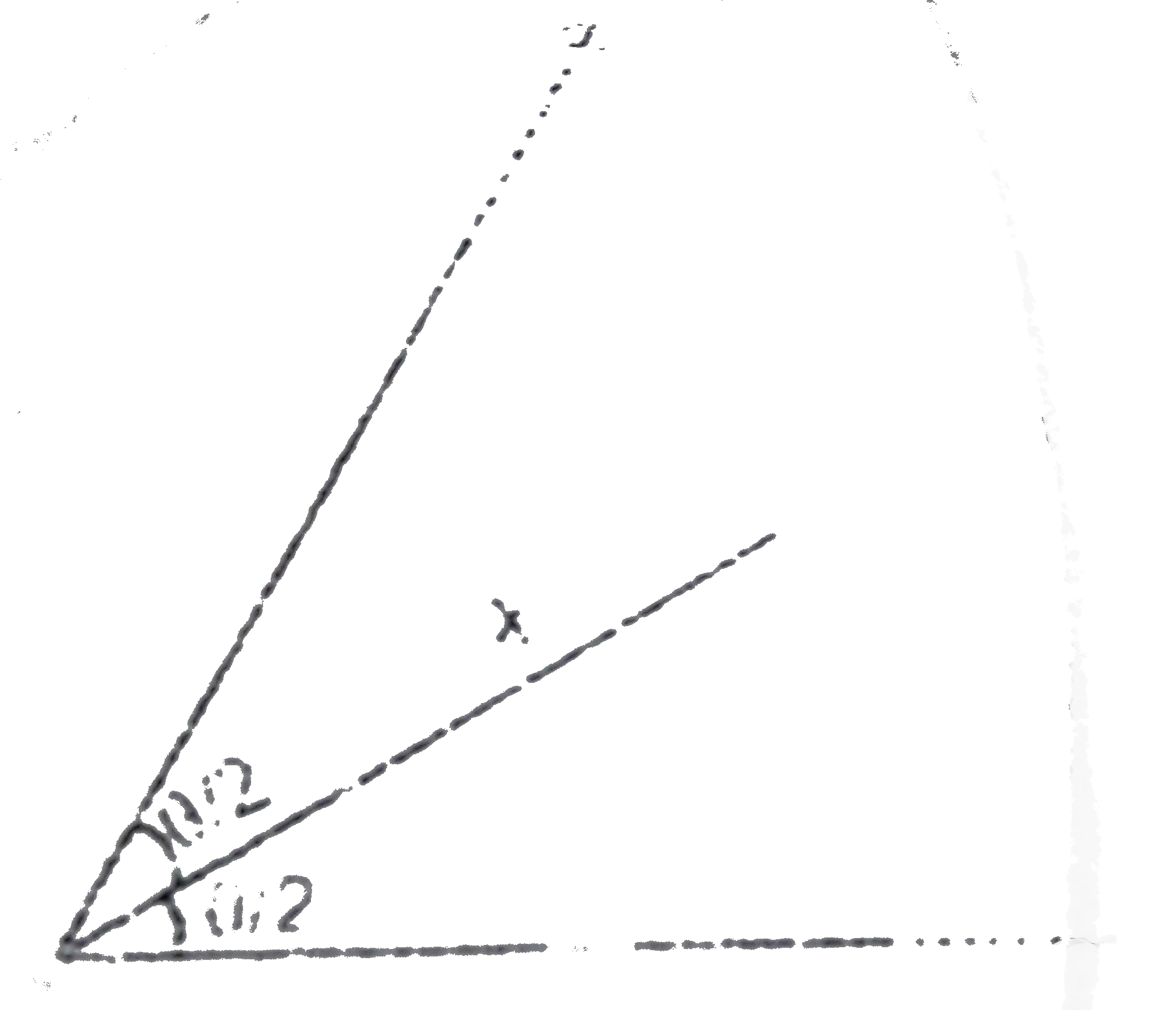 Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙
Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙A long wire carrying a current i is bent to form a plane angle. The magnitude of magnetic field at height d, above the point of bending
A√2μ0i4πdB3√2μ0i4πdC5√2μ0i4πdD7√2μ0i4πdTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
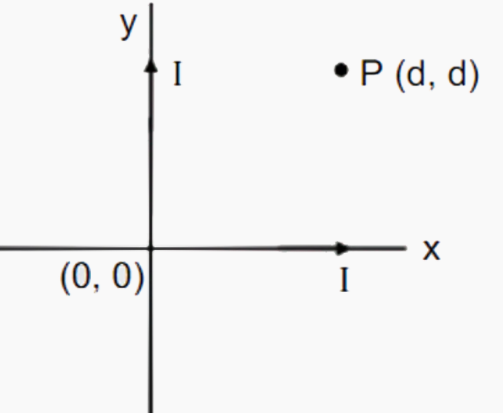 Aμ01πdBμ012πdCμ012πdDZero
Aμ01πdBμ012πdCμ012πdDZero
Current I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

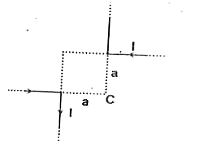
View SolutionTwo inflinitely long wires carrying current I, are bent as shown in the figure. Find the magnetic induction at point C.
View SolutionA long straight wire carries a current of 35A. What is the magnetic of the field →B at a point 20cm from the wire?
View SolutionFind magnitude and direction of magnetic field at point P in the following cases.
(a)
(b)
P is the centre of square.
(c)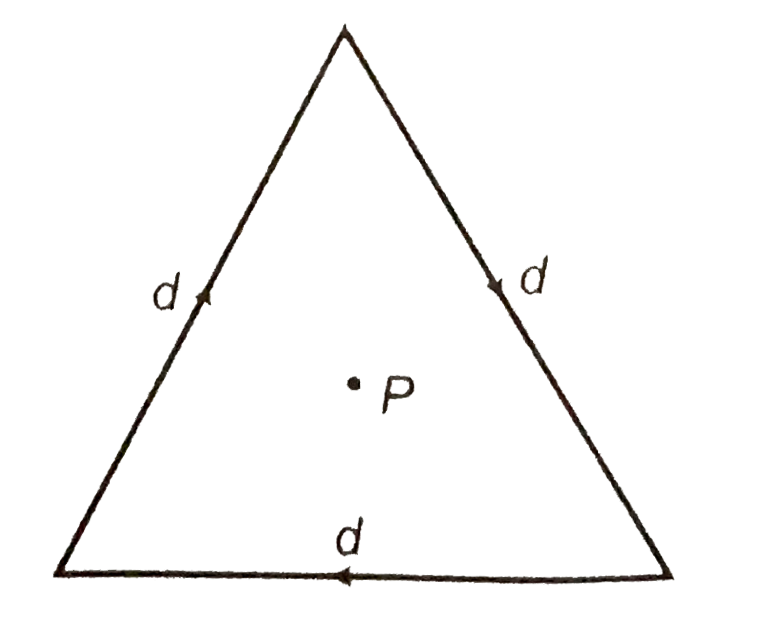
P is the centre of equilateral triangle.
(d)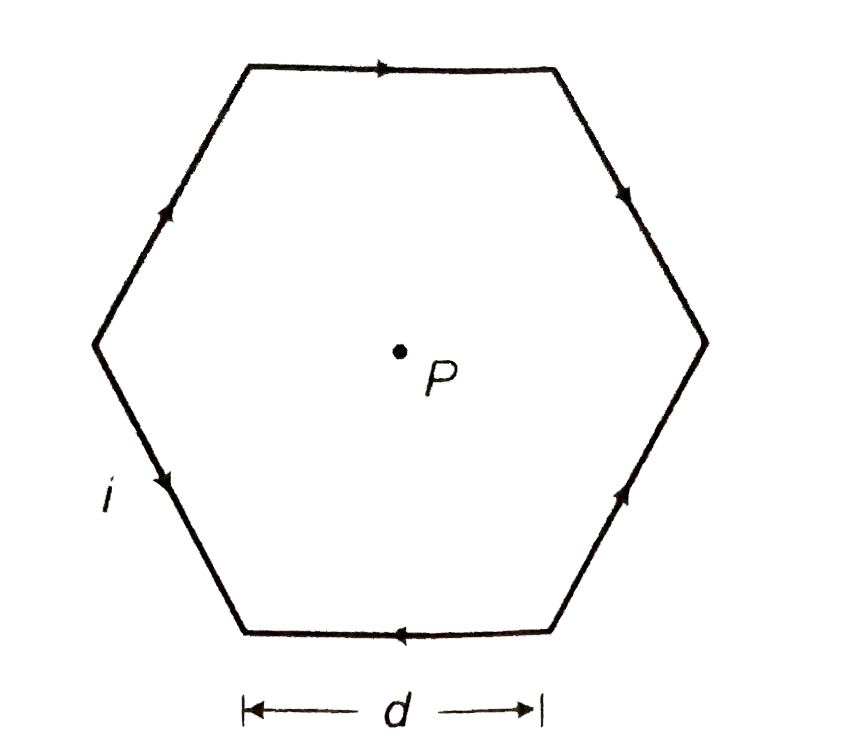
P is the centre of regular hexagon.
(e)
P is the centre of rectangular loop.
(f)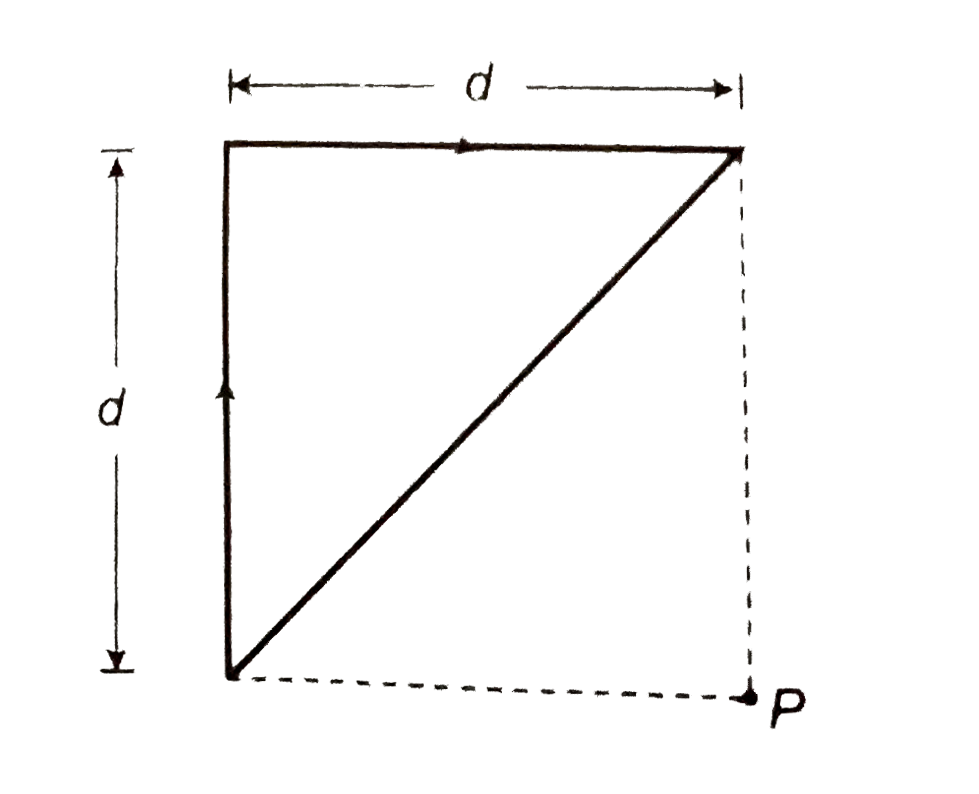
(g) A long wire carrying a current i is bent to from a plane angle θ. Find magnetic field at a point on the bisector of this angle is situated at a distance d from vertex.

(h) A long, straight wire carriers a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the sector. Let B2 be the magnetic field at this point due to this section only. find the value of d/l so that B2 differes from B1 by 1%.
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

View Solution

