The magnetic field at the point of intersection of diagonals of a square wire loop of side L carrying a current I is
μ0IπL
2μ0IπL
√2μ0IπL
2√2μ0IπL
The correct Answer is:D
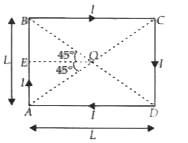
From figure, tan45∘=BEOEorOE=BE=L2
The magnetic field at point O due to current I through one side AB of the square ABCD will be
B1=μ0I4π(L2)[sin45∘+sin4520=μ02I4πL[2√2]=μ02√2I4πLOx
The total magnetic field at point O due to current I through all the foure sides of a square will be
B=4B1=μ02√2IπL
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENTBOOK - MTG-WBJEECHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - WB JEE Previous Years Questions
22 Videos
- LAWS OF MOTION BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
2 Videos
- MAGNETICSBOOK - MTG-WBJEECHAPTER - MAGNETICSEXERCISE - WB JEE Previous Years Questions (Category 3: One or More than one Option)
2 Videos
Similar Questions
The magnetic field at the point of intersection of diagonals of a square loop of side L carrying a current I is measured, Let the measured value be Nμ0IπL. What will be the value of N ?
View SolutionMagnetic field induction at the centre O of a square loop of side a carrying current I as shown in figure.
View Solution
Knowledge Check
The magnetic field at the point of intersection of diagonals of a square loop of side L carrying a current I is :
Aμ0LπLBμ0LπLC√2μ0LπLD2√2μ0LπLThe magnetic field at the point of intersection of diagonals of a square loop of side L carrying a current I is :
Aμ0LπLBμ0LπLC√2μ0LπLD2√2μ0LπLMagnetic field at the centre of coil of n turns, bent in the form of a square of side 2l, carrying current i, is
A0.5×10−5TB1.25×10−4TC3.0×10−5TD4×10−5T
Find the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
View SolutionThe magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is
View SolutionThe magnetic field at centre of a hexagonal coil of side l carrying a current I is

View SolutionMagnetic field induction at the centre of a square loop of side 'a' carrying current I as shown in figure is
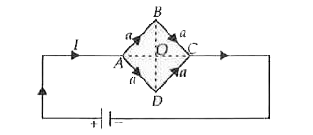
View SolutionThe magnetic field at the point O in the following current carrying square loop at the centre will be

View Solution
