A square of diagonal 18 cm is inscribed in a circle. Find the area included in the circle but not in the square.
The correct Answer is:92.57 cm2
Step by step video, text & image solution for A square of diagonal 18 cm is inscribed in a circle. Find the area included in the circle but not in the square. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBook:VK GLOBAL PUBLICATIONChapter:AREAS RELATED TO CIRCLESExercise:Proficiency Exercise (Long Answer Questions)
Explore 19 Videos
- AREAS RELATED TO CIRCLESBook:VK GLOBAL PUBLICATIONChapter:AREAS RELATED TO CIRCLESExercise:Self -Assessment Test
Explore 11 Videos
- AREAS RELATED TO CIRCLESBook:VK GLOBAL PUBLICATIONChapter:AREAS RELATED TO CIRCLESExercise:Proficiency Exercise (Short Answer Questions -I)
Explore 13 Videos
- ARITHMETIC PROGRESSIONS Book:VK GLOBAL PUBLICATIONChapter:ARITHMETIC PROGRESSIONS Exercise:SELF ASSESSMENT TEST
Explore 10 Videos
Similar Questions
Knowledge Check
A square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .
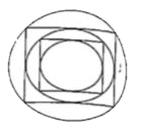
What is the sum of areas of all the squares shown in the figure ?A3R2B3√2R2C3√2R2Dnone of theseA square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .
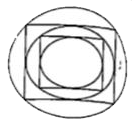
What is the ratio of sum of circumference of all the circles to the sum of perimeters of all the squares ?A(2+√3)πRB(3+√2)πRC3√3πRDnone of theseA square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .
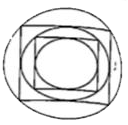
What is the radius of the inner - most circle ?AR2BR√2C√2RDnone of these
In Fig 1, a square of diagonal 8 cm is inserted in a circle. Find the area ol the shaded region.

View SolutionIf a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
View SolutionA square ABCD is inscribed in a circle of radius r. Find the area of the square.
View SolutionIn the figure given below, ABCD is a square of side 10 cm and a circle is inscribed in it. Find the area of the shaded part as shown in the figure.
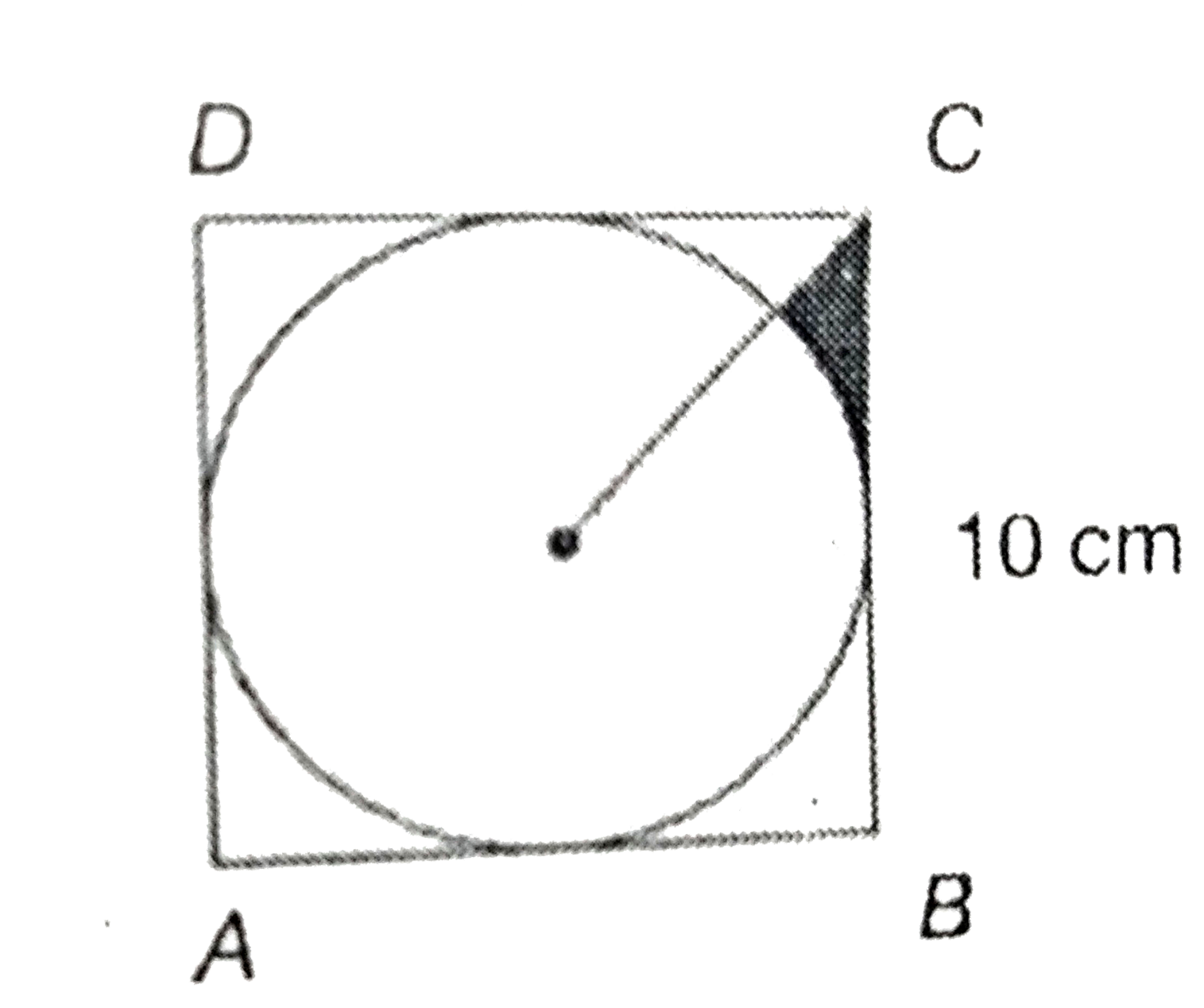
View SolutionA circle is incribed in a square. Find the ratio of area of circle to area of square.
View Solution

