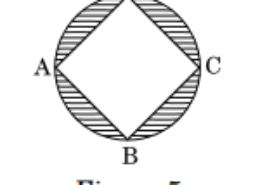
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.

Let the side of a square be a and the radius of circle be r.
Given that, length of diagonal of square = 8cm
⇒a√2=8
⇒a=4√2cm
Now, Diagonal of a square = Diameter of a circle
⇒ Diameter of circle = 8
⇒ Radius of circle = r = Diameter2
⇒r=82=4cm
∴ Area of circle = πr2=π(4)2
= 16π×cm2
and Area of square = a2=(4√2)2
32cm2
So, the area of the shaded region = Area of circle- Area of square
= (16π−32)cm2
Hence, the required area of the shaded region is (16π−32)cm2
Topper's Solved these Questions
Similar Questions
In Fig 1, a square of diagonal 8 cm is inserted in a circle. Find the area ol the shaded region.

View SolutionFind the area of the shaded region in Figure.
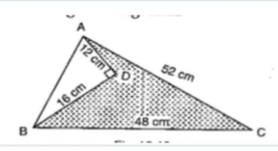
View SolutionFind the area of the shaded region in figure.

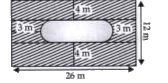
View SolutionFind the area of the shaded region in figure .
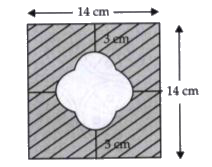
View SolutionIn figure , find the area of the shaded region
View SolutionIn given figure a semicircle of radius 7cm is inscribed in a rectangle. Find the area of the shaded region.
View SolutionIn the given giure, ABCD is a square with side 2√2 and inscribed in a circle. Find the area of the shaded region. (Use π = 3.14)
View SolutionIn Fig. 15.80, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π=3.14 ) (FIGURE)
View SolutionA square of diagonal 18 cm is inscribed in a circle. Find the area included in the circle but not in the square.
View SolutionIn the adjoining figure, PQR is an equilateral triangle inscribed in a circle of radius 7cm. Find the area of the shaded region.
View Solution

