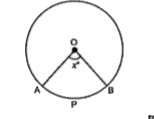
In fig., O is the centre of a circle. The area of sector OAPB is of the area of the circle. Find x.
The correct Answer is:
Step by step video, text & image solution for In fig., O is the centre of a circle. The area of sector OAPB is (5)/(18) of the area of the circle. Find x. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
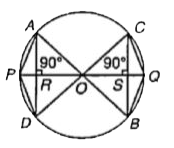
In the adjoining figure O is the centre of the circle. ∠AOD=120?∘. If the radius of the circle be 'r', then find the sum of the areas of quadrilaterals AODPandOBQC :
 A√32r2B3√3r2C√3r2Dnone of these
A√32r2B3√3r2C√3r2Dnone of theseThe area of a sector of a circle is 77 sq cm and the angle of the sector is 45∘. Find the radius of the circle.
A7 cmB14 cmC21 cmD28 cm
In Fig. 2.47, O is the centre of the circle.
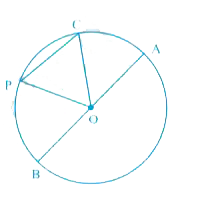
Shade sectors OAC and OPB.
View SolutionThe ratio of the area of a sector of a circle to the area of the circle is 1:4. If the area of the circle is 154cm2, the perimeter of the sector is
View SolutionIf the following figure, O is the centre of the circle and XO is perpendicular to OY. If the area of the triangle XOY is 32, then the area of the circle is :
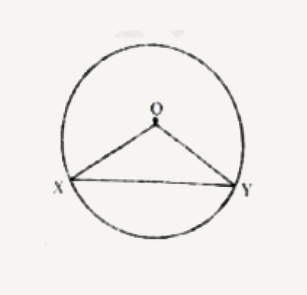
View SolutionFind the area of the segment of a circle, given that the angle of the sector is 120o and the radius of the circle is 21 cm. (Take π=22/7)
View SolutionIn the figure, O is the centre of the circle. ∠POQ=90∘ .
The area of the shaded region is 126cm2. Find the radius of the circle.
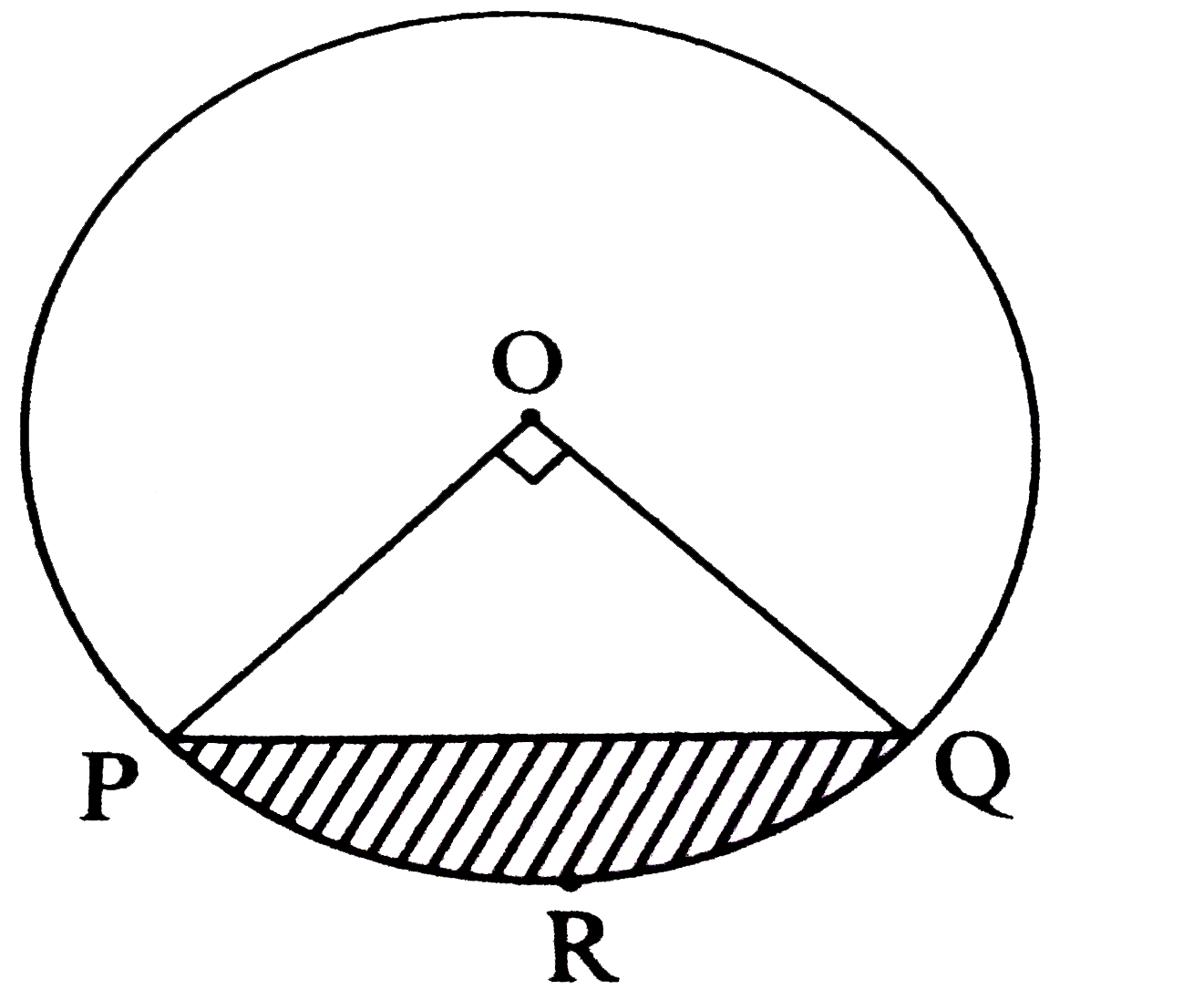
View SolutionRadius of a sector of a circle is 7 cm. If measure of arc of the sector is 30∘find the area of the sector
View Solution