Two identical resistors of magnitude R and two identical capacitors of magnitude C are used to form an RC circuit. In which case the time constant of that RC circuit is the highest?
Two resistors and two capacitors connected in series with a power supply
Two resistors and two capacitors connected in parallel with a power supply
Two resistors connected in parallel, two capacitors connected in parallel, and those two combinations are connected in series with a power supply
Two resistors connected in series, two capacitors connected in parallel, and those two combinations are connected in series with a power supply
The correct Answer is:D
To determine in which case the time constant of the RC circuit is the highest, we need to analyze how resistors and capacitors are connected in the circuit. The time constant (τ) of an RC circuit is given by the formula:
τ=Req⋅Ceq
where Req is the equivalent resistance and Ceq is the equivalent capacitance.
Step 1: Identify the configurations
We have two identical resistors (R) and two identical capacitors (C). The configurations can be:
1. Both resistors in series and both capacitors in series.
2. Both resistors in parallel and both capacitors in parallel.
3. Both resistors in series and both capacitors in parallel.
4. Both resistors in parallel and both capacitors in series.
Step 2: Calculate equivalent resistance and capacitance for each configuration
1. Both resistors in series and both capacitors in series:
- Req=R+R=2R
- Ceq=C2
- Time constant: τ=(2R)⋅(C2)=RC
2. Both resistors in parallel and both capacitors in parallel:
- Req=R2
- Ceq=C+C=2C
- Time constant: τ=(R2)⋅(2C)=RC
3. Both resistors in series and both capacitors in parallel:
- Req=2R
- Ceq=C+C=2C
- Time constant: τ=(2R)⋅(2C)=4RC
4. Both resistors in parallel and both capacitors in series:
- Req=R2
- Ceq=C2
- Time constant: τ=(R2)⋅(C2)=RC4
Step 3: Compare the time constants
From the calculations:
- Configuration 1: τ=RC
- Configuration 2: τ=RC
- Configuration 3: τ=4RC
- Configuration 4: τ=RC4
The highest time constant is found in Configuration 3, where the resistors are in series and the capacitors are in parallel, yielding τ=4RC.
Conclusion
The configuration that gives the highest time constant is when two resistors are connected in series and two capacitors are connected in parallel.
---
We have two identical resistors (R) and two identical capacitors (C). The configurations can be:
1. Both resistors in series and both capacitors in series.
2. Both resistors in parallel and both capacitors in parallel.
3. Both resistors in series and both capacitors in parallel.
4. Both resistors in parallel and both capacitors in series.
- Req=R+R=2R
- Ceq=C2
- Time constant: τ=(2R)⋅(C2)=RC
- Req=R2
- Ceq=C+C=2C
- Time constant: τ=(R2)⋅(2C)=RC
- Req=2R
- Ceq=C+C=2C
- Time constant: τ=(2R)⋅(2C)=4RC
- Req=R2
- Ceq=C2
- Time constant: τ=(R2)⋅(C2)=RC4
From the calculations:
- Configuration 1: τ=RC
- Configuration 2: τ=RC
- Configuration 3: τ=4RC
- Configuration 4: τ=RC4
The configuration that gives the highest time constant is when two resistors are connected in series and two capacitors are connected in parallel.
Topper's Solved these Questions
- CIRCUITSBook:RESNICK AND HALLIDAYChapter:CIRCUITSExercise:Practice Questions (More than One Correct Choice Type)
Explore 12 Videos
- CIRCUITSBook:RESNICK AND HALLIDAYChapter:CIRCUITSExercise:Practice Questions (Linked Comprehension)
Explore 11 Videos
- CIRCUITSBook:RESNICK AND HALLIDAYChapter:CIRCUITSExercise:Problems
Explore 45 Videos
- CENTER OF MASS Book:RESNICK AND HALLIDAYChapter:CENTER OF MASS Exercise:Practice Questions (Integer )
Explore 4 Videos
- CIRCULAR MOTIONBook:RESNICK AND HALLIDAYChapter:CIRCULAR MOTIONExercise:CHECK POINTS
Explore 6 Videos
Similar Questions
Knowledge Check
Two identical resistors of magnitude R and two identical capacitors of magnitude C are used to form an RC circuit. In which case the time constant of the RC circuit is the highest?
ATwo resistors and two capacitors connected in series with a power supply.BTwo resistors and two capacitors connected in parallel with a power supply.CTwo resistors connected in parallel, two capacitors connected in parallel, and those two combinations are in series with a power supplyDTwo resistors connected in series, two capacitors connected in parallel and those two combinations are connected in series with a power supply.The time constant of C-R circuit is
A1CRBCRCCRDRCThe capacitive time constant of the RC circuit shown in the figure.
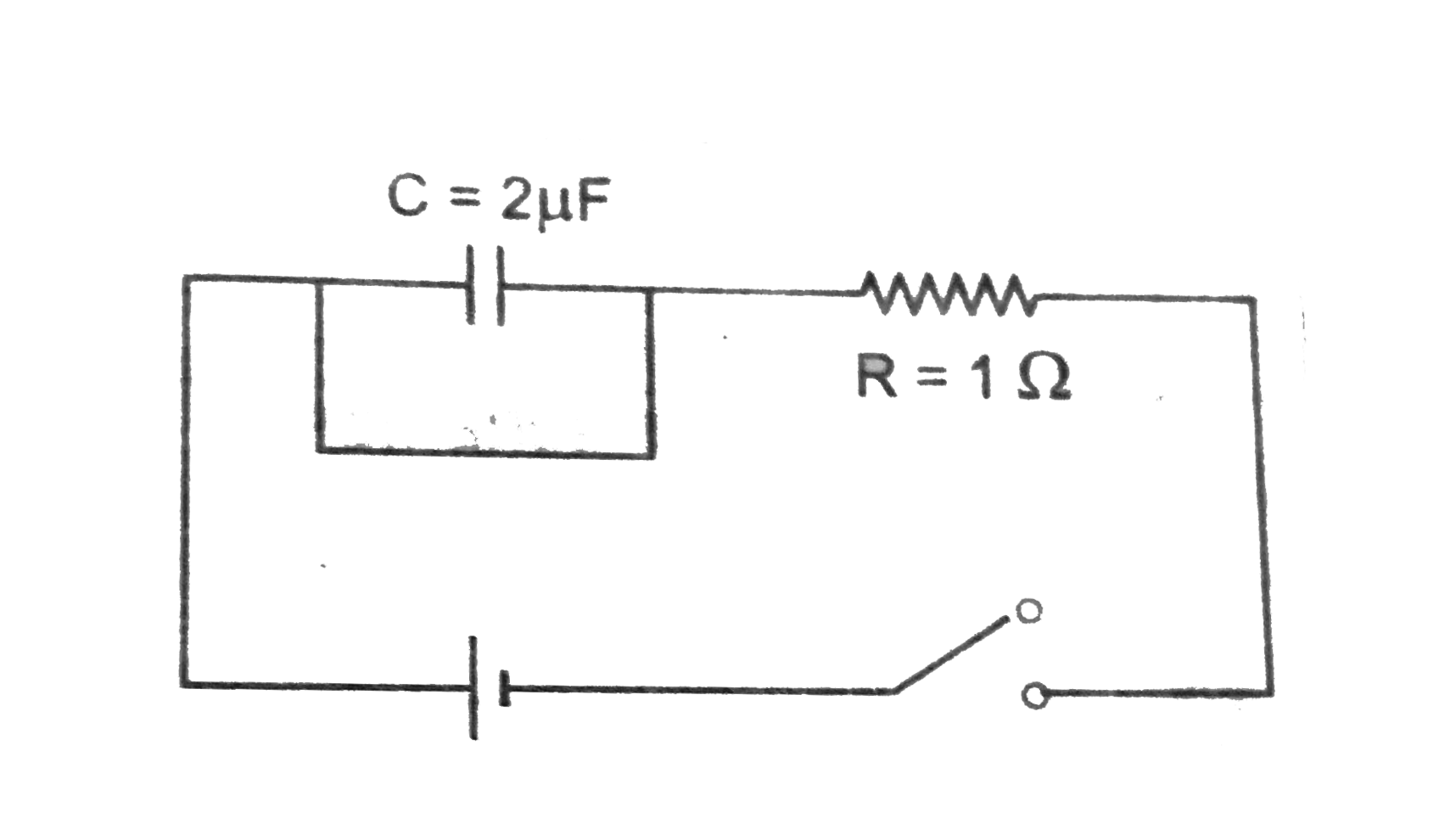 AzeroBinfinityC2 sD2μs
AzeroBinfinityC2 sD2μs
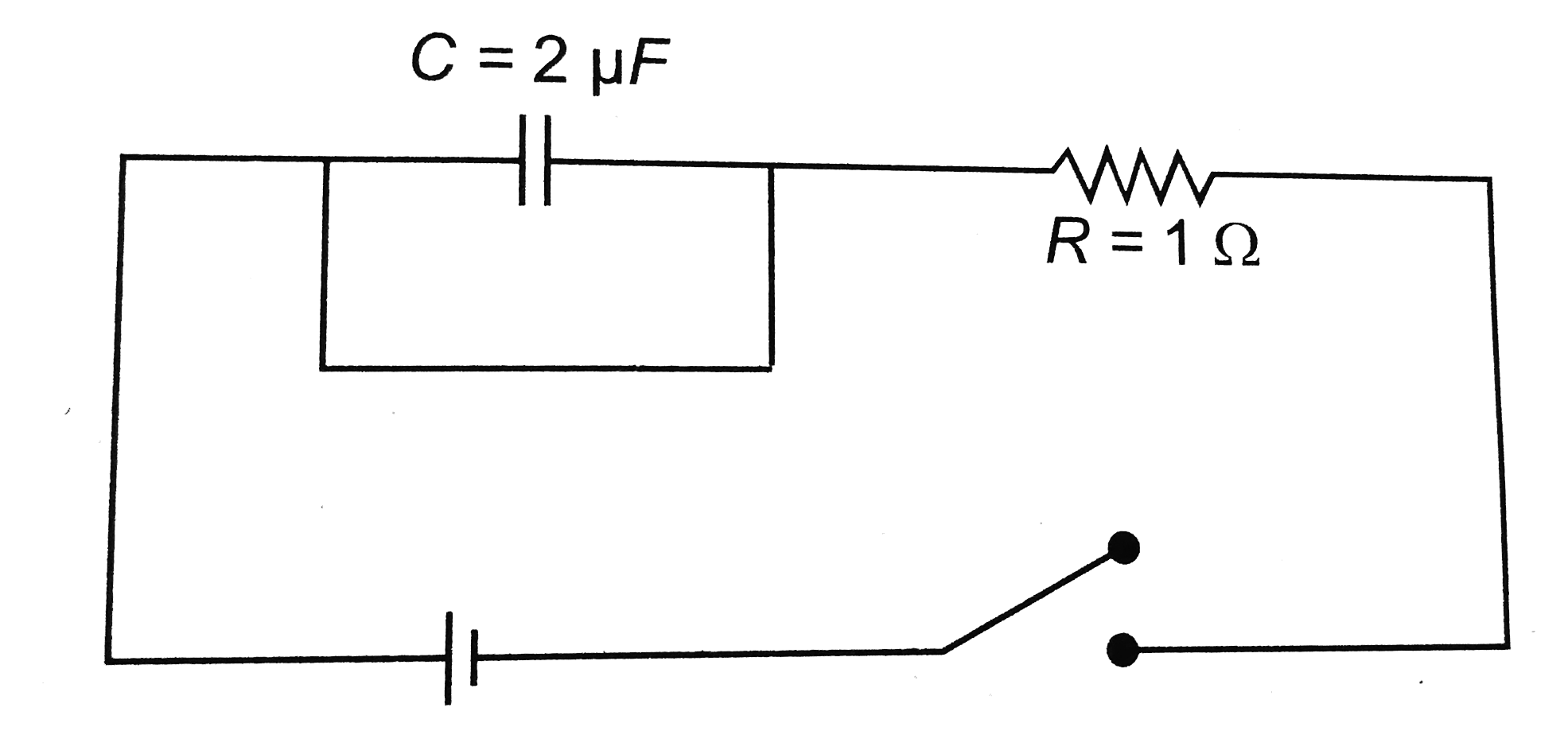
The capacitive time constant of the RC circuit shown in the figure is
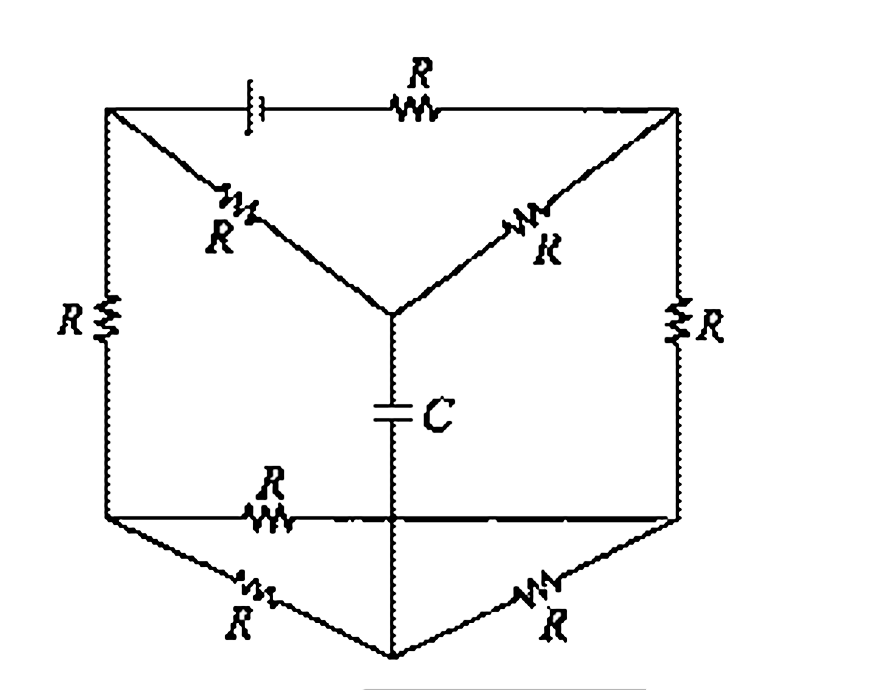
View SolutionWhat is equivalent time constant of RC circuit shown in fignre-3.340 ?
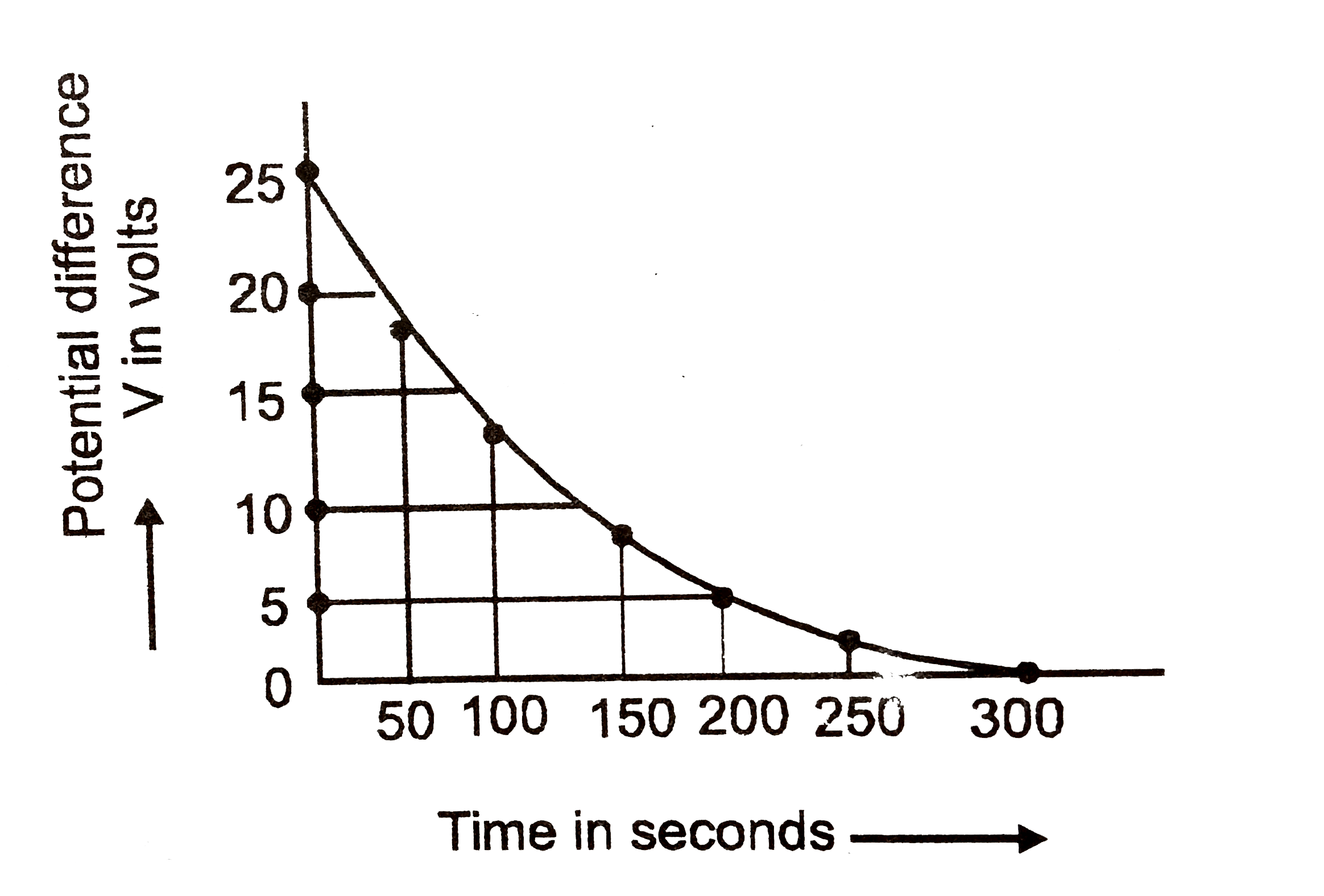
View SolutionThe figure shows an experimental plot discharging of a capacitor in an RC circuit. The time constant of this circuit lies between:
View SolutionIn the circuit shown in the diagram, E is the e.m.f of the cell, connected to two resistances. Each of magnitude R and a capacitor of capacitance C as shown in the diagram. If the switch key K is closed at time t=0, the growth of potential V across the capacitor with be correctly given by
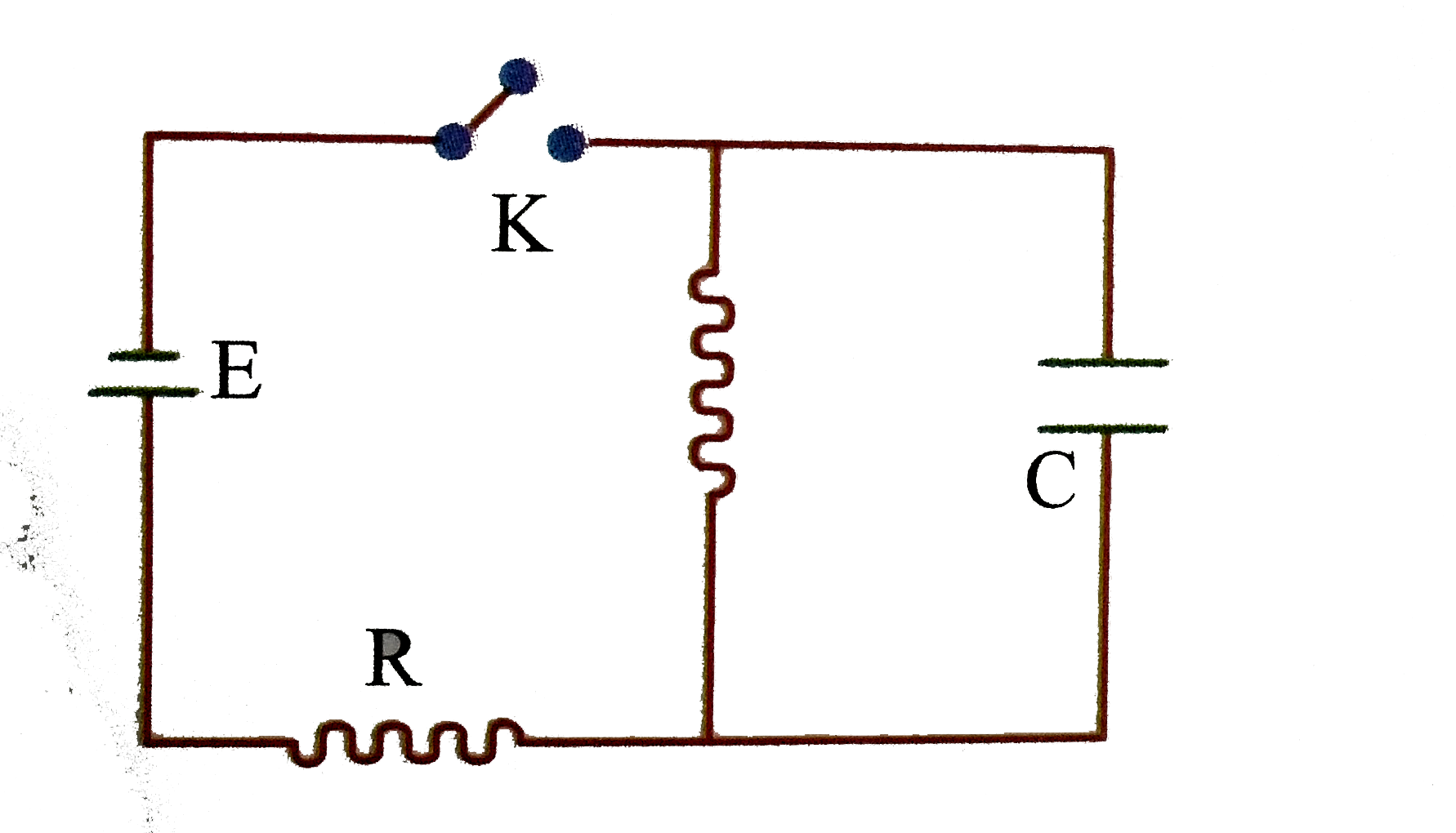 .
.
View SolutionA capacitor C is connected to two equal resistances as shown in the figure. Consider the following statemets
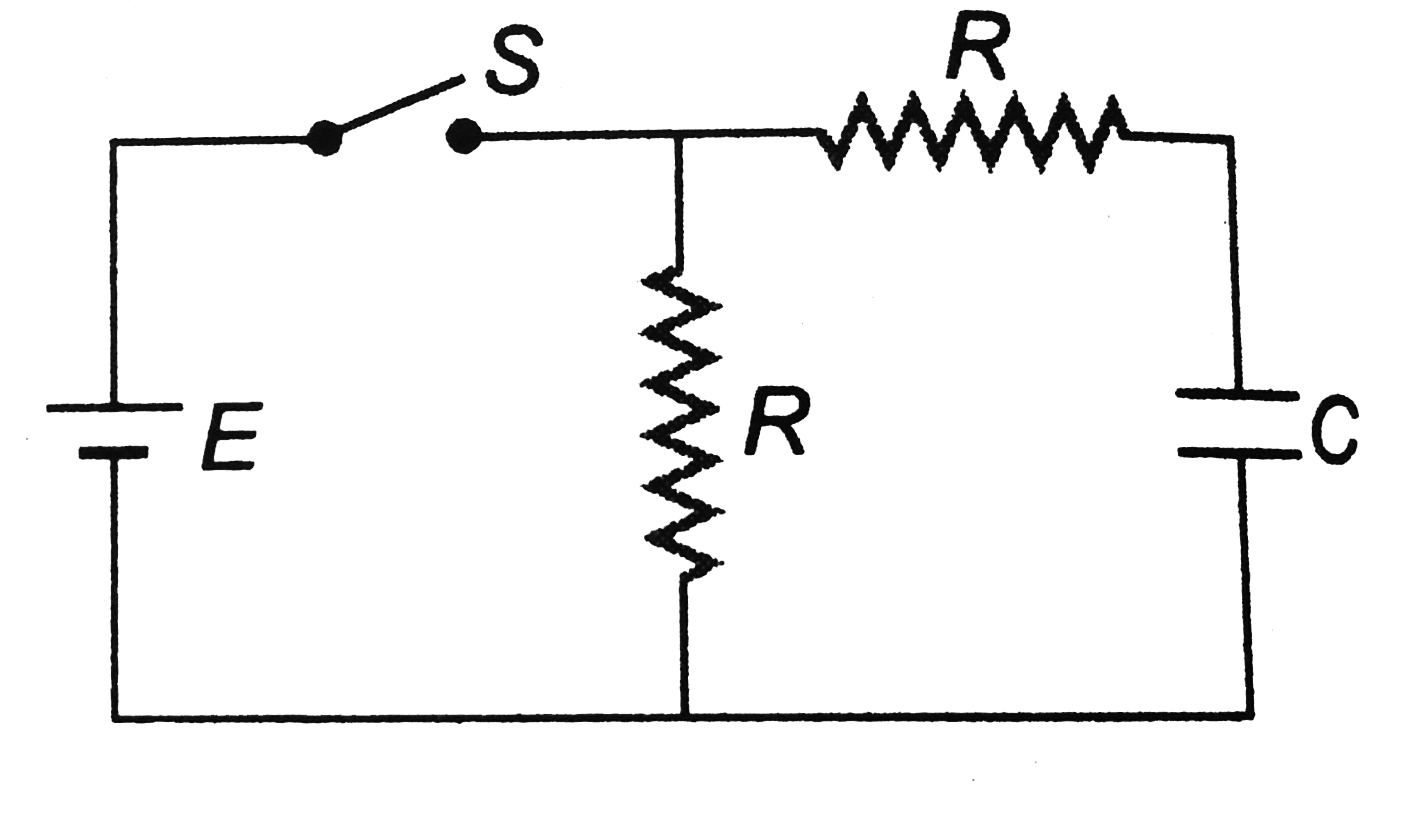
i. At the time of charging of capacitor time constant of the circuit is 2CR
ii. At the time of discharging of the capacitor the time constant of the circuit is CR
iii. At the time of discharging of the capacitor the time constant of the circuit is 2CR
iv At the time of charging of the capacitor the time constant of the circuit is 2CR
View Solution

