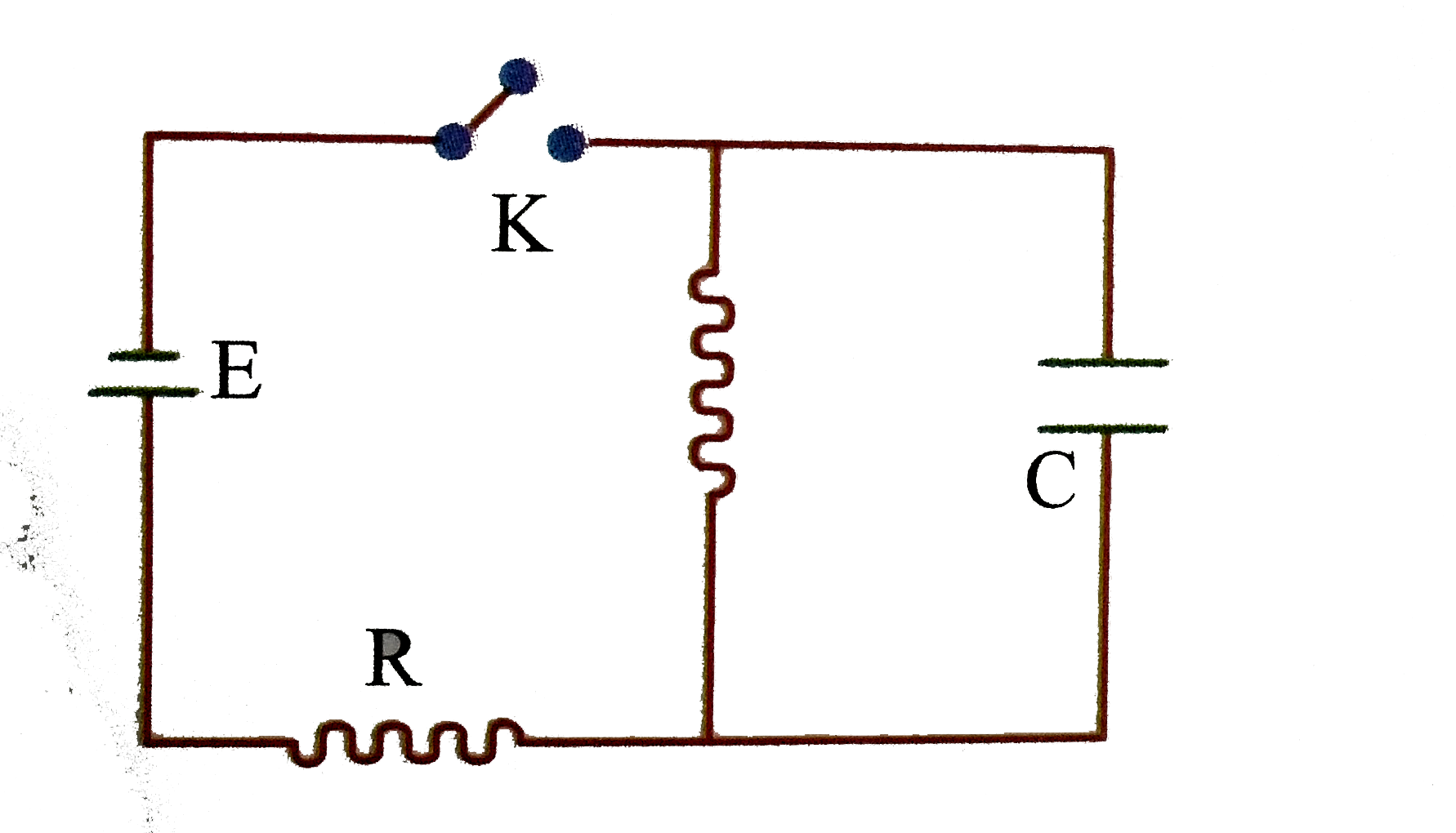
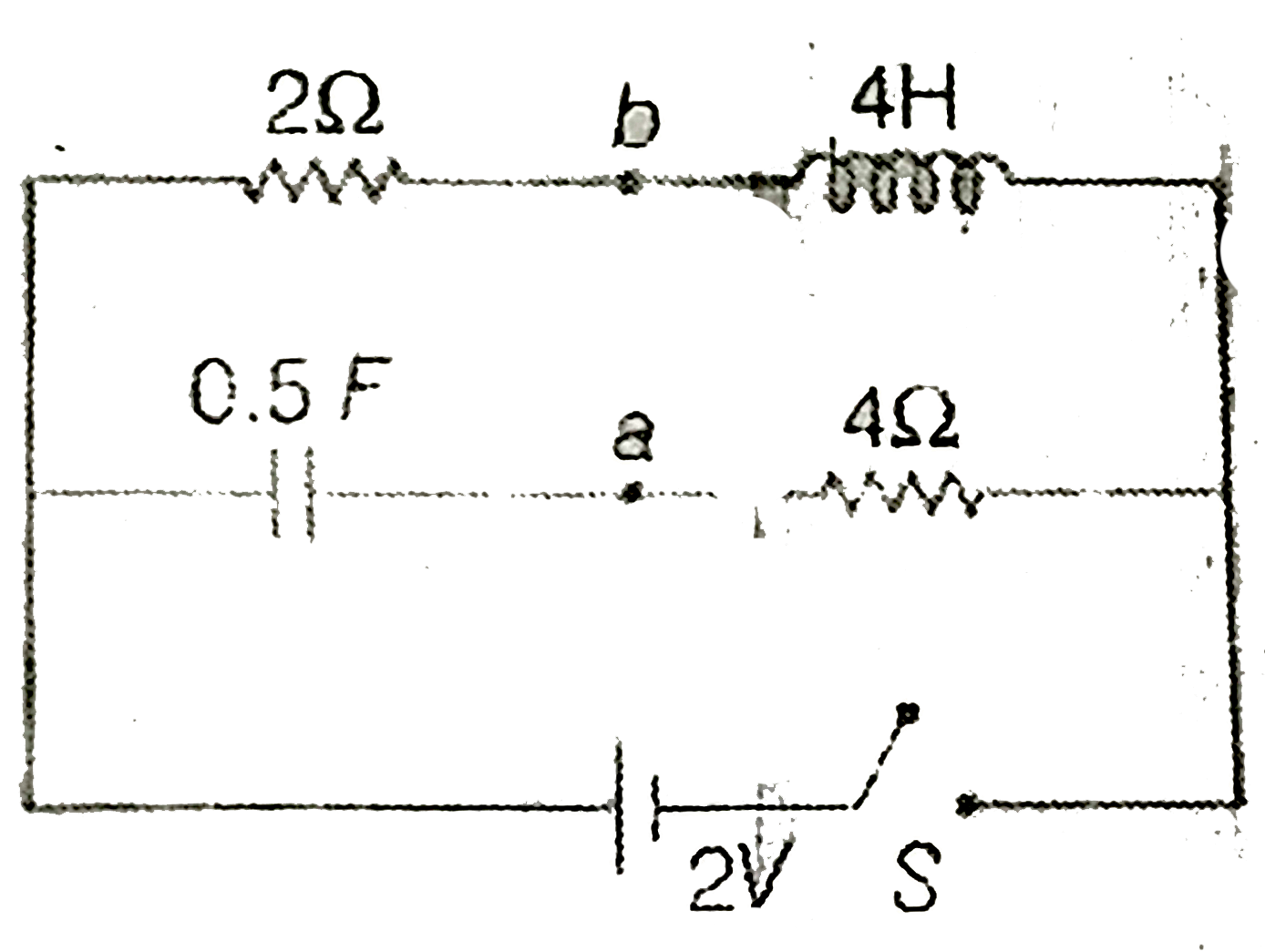In the circuit shown in the diagram, E is the e.m.f of the cell, connected to two resistances. Each of magnitude R and a capacitor of capacitance C as shown in the diagram. If the switch key K is closed at time t=0, the growth of potential V across the capacitor with be correctly given by
 .
.
V(t)=E[1−exp(−tRC)]
V(t)=E2[1−exp(−2tRC)]
V(t)=E[1−exp(−2tRC)]
V(t)=E2[1−exp(−tRC)]
The correct Answer is:B
The given problem may be approached in a simplified manner of the following considerations. Since the resistances R and R are in seriea with the battery, the potential difference across R(which charges the capacitor) will have maximum value E/2. Also, if the battery is absent, and the (charged) capacitor were to discharge, the two resistors R and R will be connected in parallel (i.e) effective resistance across the capacitor is (R/2) and hence the time-constant in the cirstant in the circuit is τ=RC/2. Thus the growth of potential in the capacitor will be given by
V(t)=E2[1−exp(−tτ)]
=E2[1−exp(−2tRC)].
Topper's Solved these Questions
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:Level-VI
Explore 28 Videos
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:Subjective
Explore 9 Videos
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:NCERT Based
Explore 13 Videos
- ATOMS Book:NARAYNAChapter:ATOMS Exercise:EXERCISE -4
Explore 47 Videos
- COMMUNICATION SYSTEMBook:NARAYNAChapter:COMMUNICATION SYSTEMExercise:Level-II(H.W)
Explore 25 Videos
Similar Questions
Knowledge Check
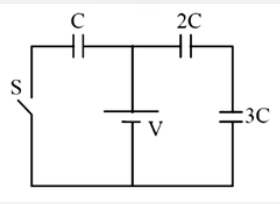
In the circuit shown each capacitor has a capcitance C. The emf of the celll is E. If the switch S is closed then
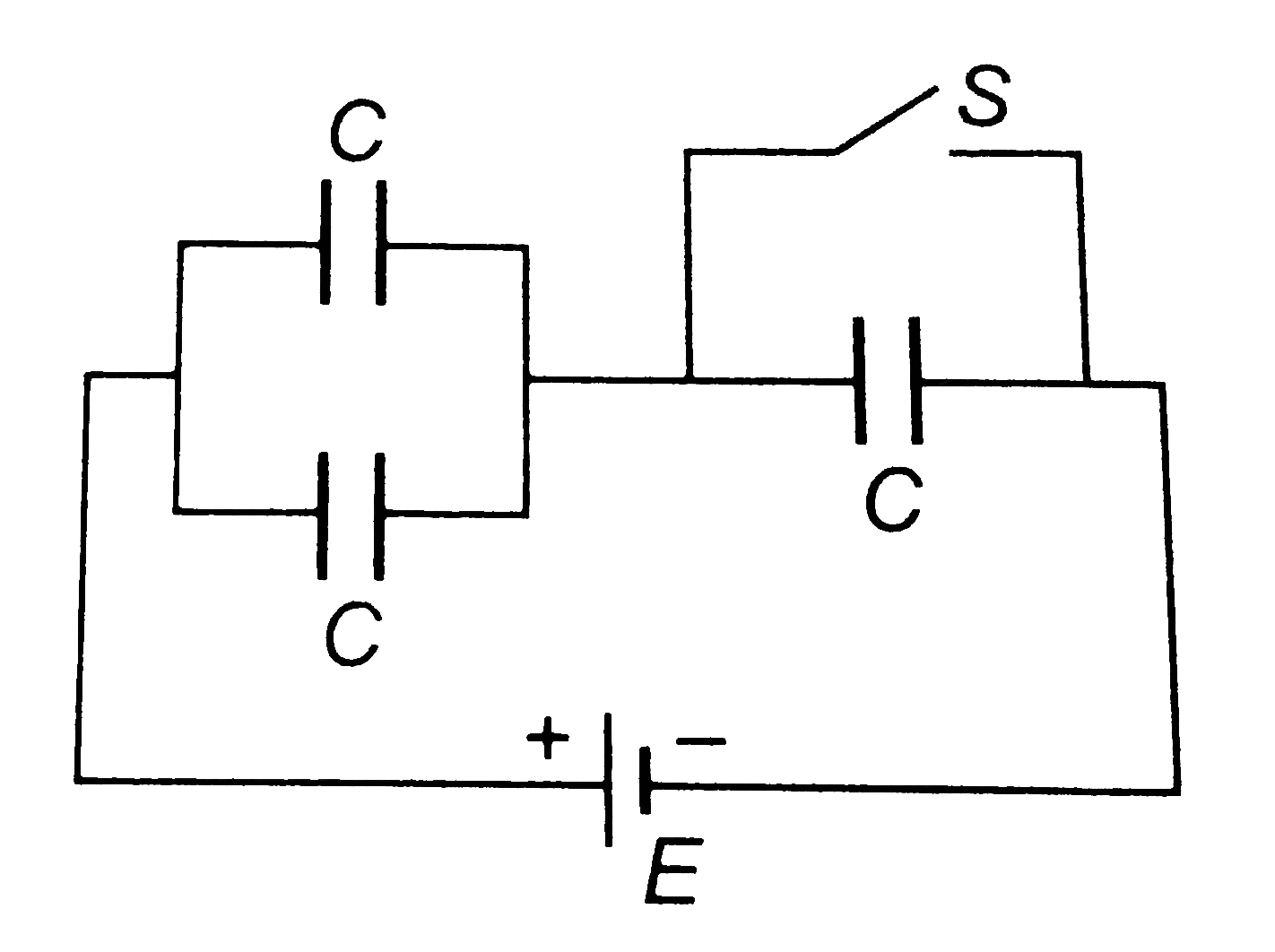 APositive charge wil flow out of the positive terminal of the cellBPositive charge will enter the positive terminal of the cellCthe amount of the charge flowing through the cell will be 13 CEDthe amount of charge flowing through the cell is (43)CE
APositive charge wil flow out of the positive terminal of the cellBPositive charge will enter the positive terminal of the cellCthe amount of the charge flowing through the cell will be 13 CEDthe amount of charge flowing through the cell is (43)CEIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant
 ARCB3RCC23RCDRCIn(23)
ARCB3RCC23RCDRCIn(23)A capacitor of capacitance C0 is charged to a potential V0 and is connected with another capacitor of capacitance C as Shown . After closing the switch S, the common potential across the two capacitors becomes V . The capacitance C is given by
 AC0(V0−V)V0BC0(V−V0)V0CC0(V+V0)VDC0(V0−V)V
AC0(V0−V)V0BC0(V−V0)V0CC0(V+V0)VDC0(V0−V)V
A capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionIn the circuit shown, the cell is ideal , with emf=15V. Ecah resistance is of 3Ω. the potential difference across the capacitor is
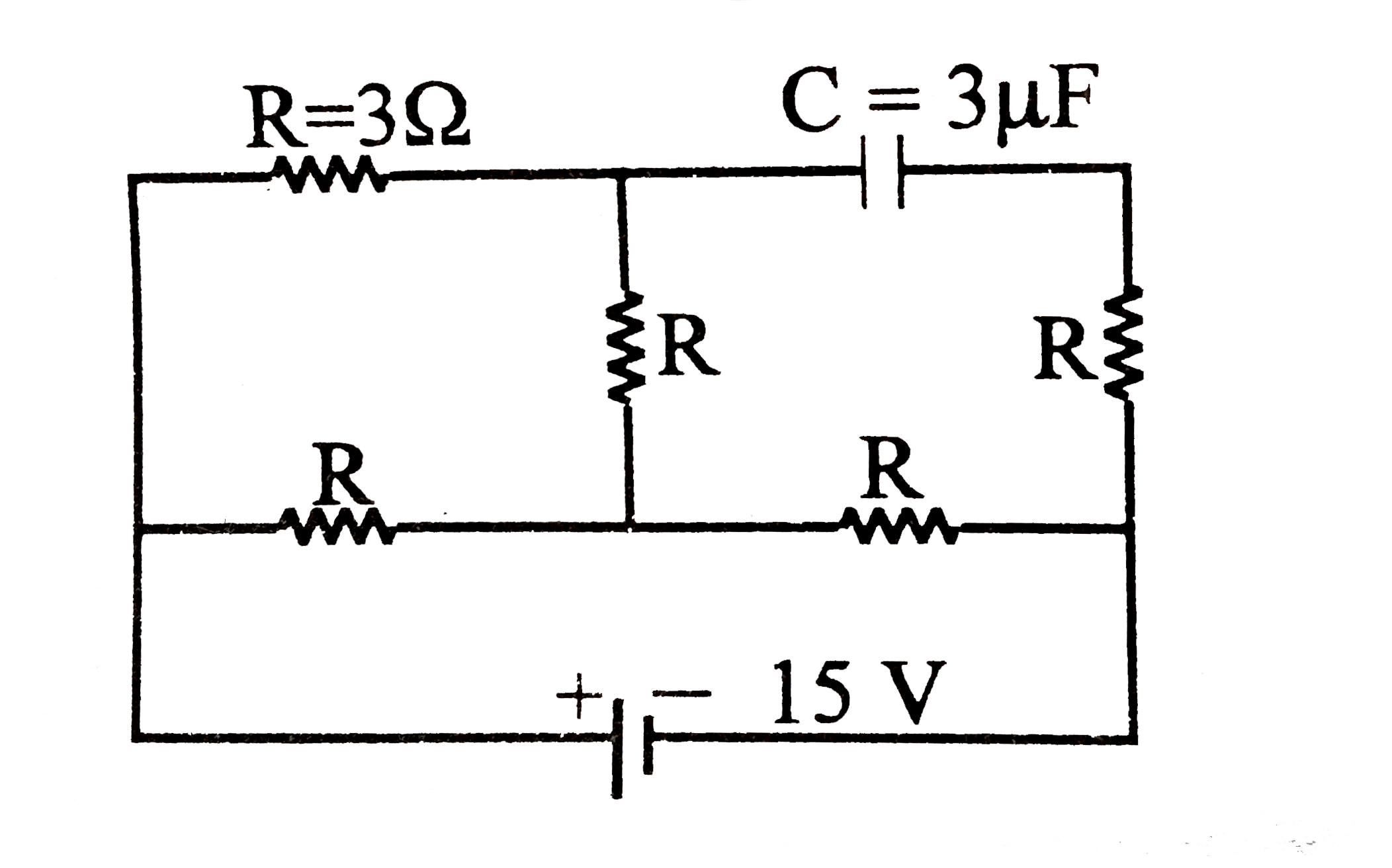
View SolutionIn the circuit shown in figure, the capacitor is charged with a cell of 5V.If the switch is closed at t=0, then at t=12s, charge on the capacitor is

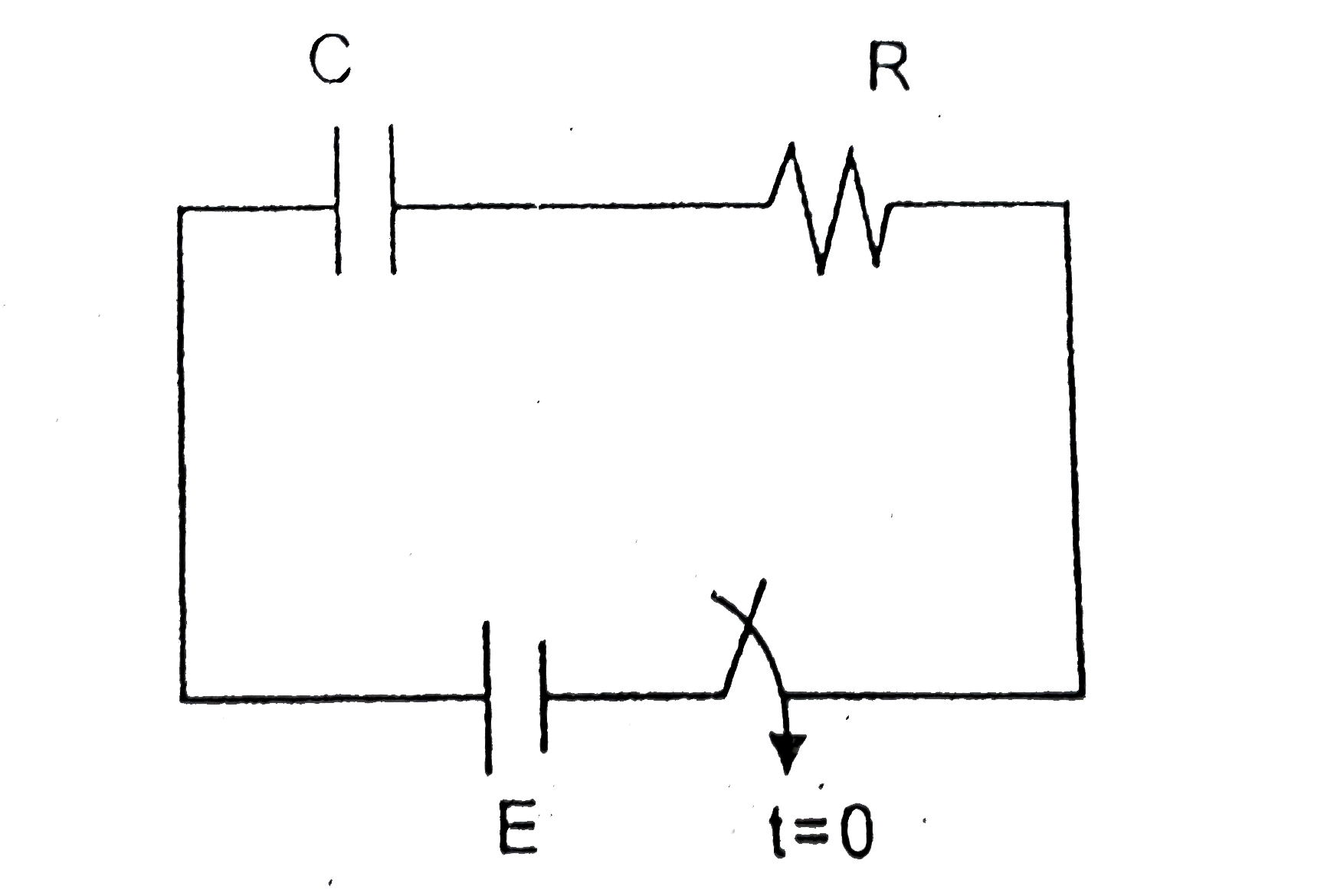
View SolutionIn the circuit shown key is closed at t=0 with capacitor initially uncharged.
View SolutionIn the circuit shown in figure switch S is closed at time t=0
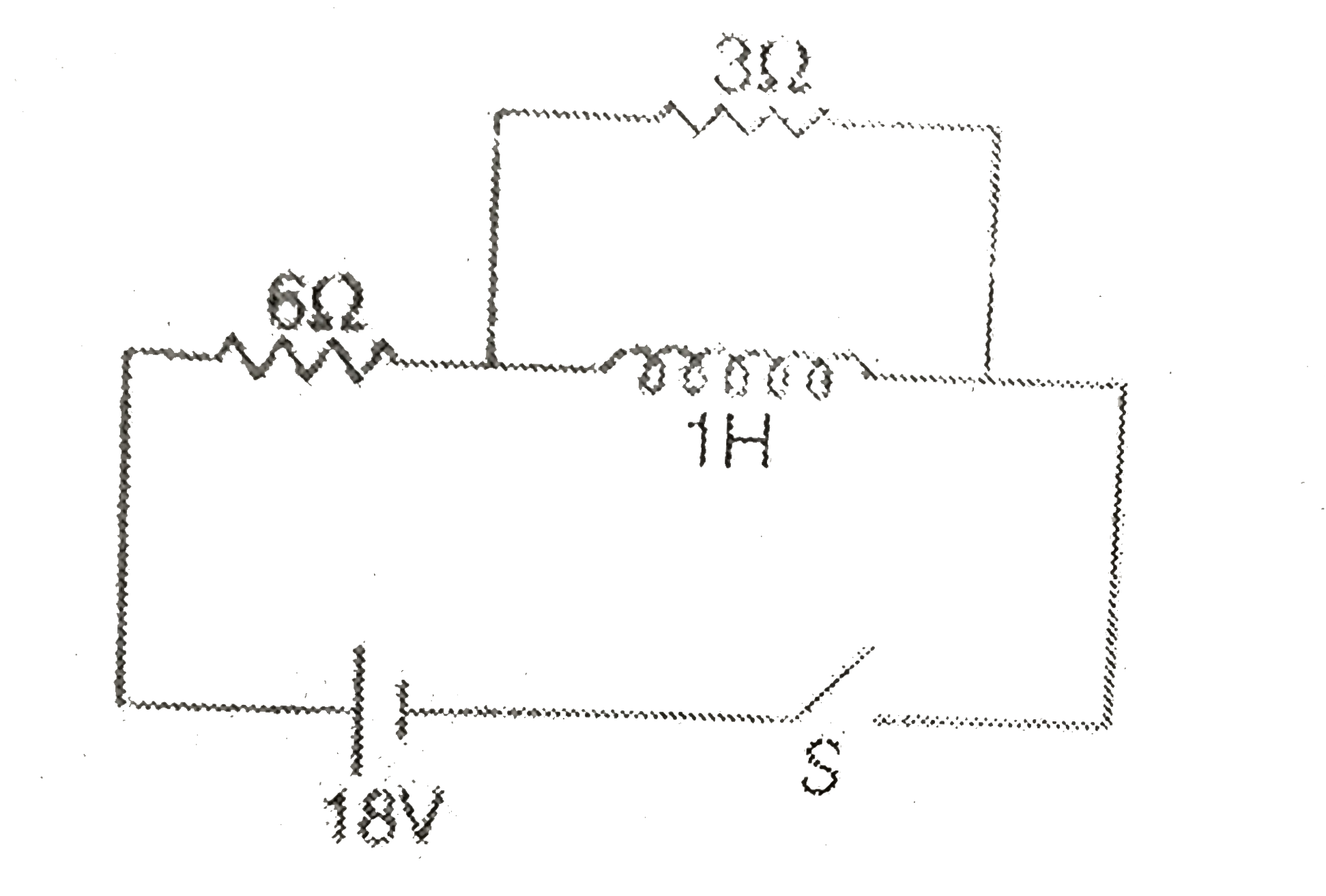
Potential difference across 3Ω resistance at time t is given by
View Solution