A capacitor of capacitance C is given a charge Q. At t=0,it is connected to an uncharged of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
Q(1−e−2tRC)
Q2(1−e−2tRC)
Q2(1−e−tRC)
Q(1−e−tRC)
The correct Answer is:B
At any instance charges on capacitors will be as shown
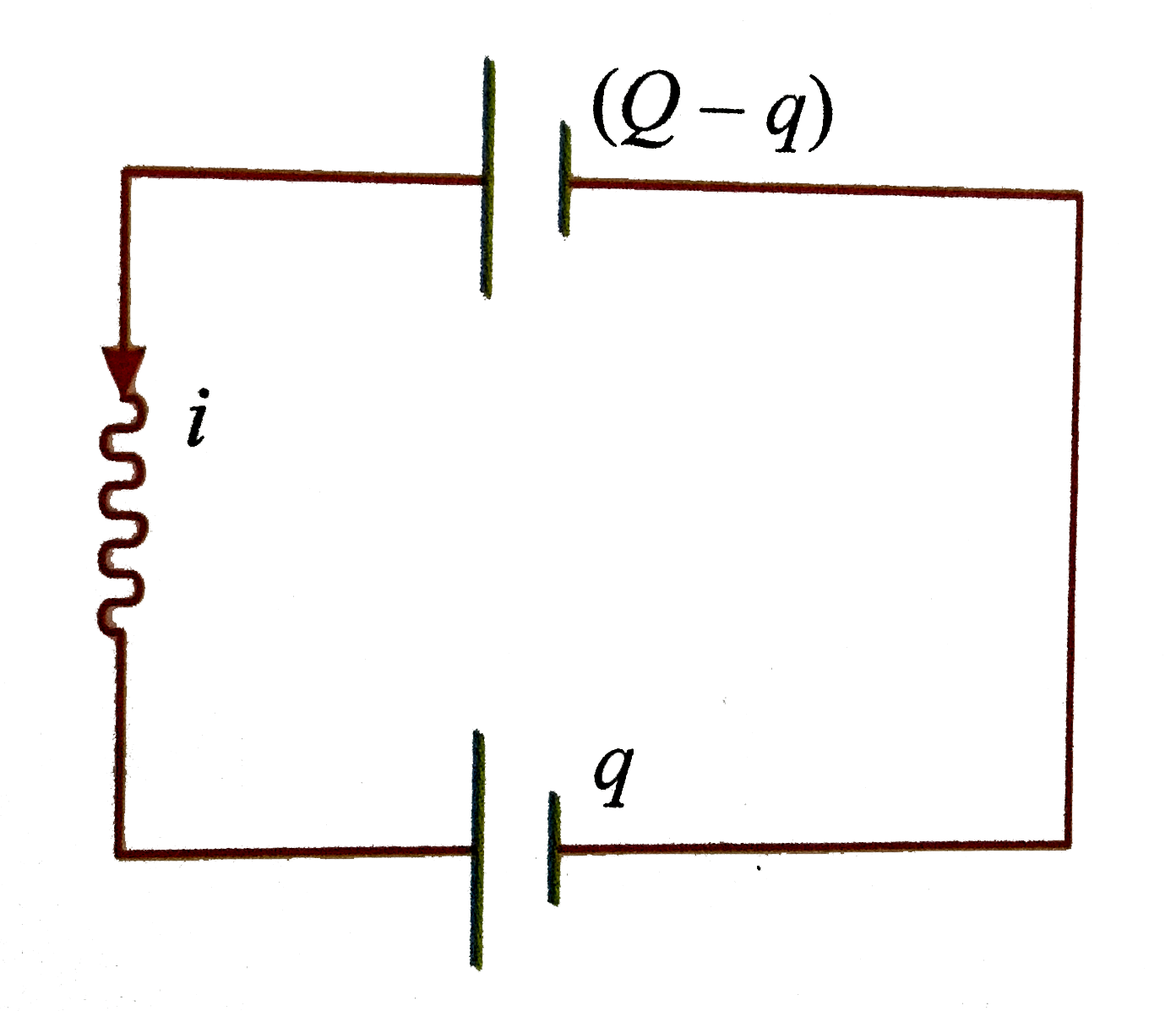
Applying KVL, we get
qC=(Q−q)C+iR=0andi=dqdt.
Topper's Solved these Questions
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:Level-VI
Explore 28 Videos
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:Subjective
Explore 9 Videos
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:NCERT Based
Explore 13 Videos
- ATOMS Book:NARAYNAChapter:ATOMS Exercise:EXERCISE -4
Explore 47 Videos
- COMMUNICATION SYSTEMBook:NARAYNAChapter:COMMUNICATION SYSTEMExercise:Level-II(H.W)
Explore 25 Videos
Similar Questions
A capacitor of capacitance C is given a charge go. At time t=0 it is connected to an uncharged capacitor of equal capacitance through a resistance R. Find the charge on the first capacitor and the second capacitor as a function of time t. Also plot the corresponding q-t graphs.
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View Solution
Knowledge Check
A capacitor of capacitance C has charge Q. it is connected to an identical capacitor through a resistance. The heat produced in the resistance is
AQ22CBQ24CCQ28CDdependent on the value of the resistanceA capacitor of capacitance C carrying charge Q is connected to a source of emf E. Finally, the charge on capacitor would be
AQBQ+CeCCEDnone of theseA capacitor of capacitance C is given charge Q and then connected in parallel to a coil of inductance L. There is no resitance in the circuit. When the charge on the capacitor becomes zero, the current in the coil will be
AQ√LCBQ√LCCQ√CLDzero
A capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance C charged by battery at V volt and then disconnected. At t = 0, it is connected to an uncharged capacitor of capacitance 2C through a resistance R. The charge on the second capacitor as a function of time is given by q=αCV3(1−e−3tβRC) then fing the value of αβ.
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V. It is then connected to another uncharged capacitor having the same capacitance. Find out the ratio of the electrostatic energy stored in the combined system to that stored initially in the single capacitor.
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V. It is then connected to another uncharged capacitor having the same capacitance. Find out the ratio of the energy stored in the combined system to that stored initially in the single capacitor.
View SolutionA capacitor of capacitance C0 is charged to potential V0. Now it is connected to another uncharged capacitor of capacitance C02. Calculate the heat loss in this process.
View Solution

