A 15 N net force is applied for 6.0 s to a 12 kg box initially at rest. What is the speed of the box at the end of the 6.0 s interval?
1.8 m/s
15 m/s
3.0m/s
7.5 m/s
The correct Answer is:D
To solve the problem step by step, we will use Newton's second law of motion and the equations of motion.
Step 1: Identify the given values
- Net force (F) = 15 N
- Mass of the box (m) = 12 kg
- Initial velocity (u) = 0 m/s (the box is initially at rest)
- Time (t) = 6.0 s
Step 2: Calculate the acceleration of the box
According to Newton's second law of motion, the net force acting on an object is equal to the mass of the object multiplied by its acceleration (F = m * a). We can rearrange this formula to find the acceleration (a):
a=Fm
Substituting the known values:
a=15N12kg
Calculating the acceleration:
a=1.25m/s2
Step 3: Use the first equation of motion to find the final velocity
The first equation of motion relates initial velocity (u), final velocity (v), acceleration (a), and time (t):
v=u+at
Since the initial velocity (u) is 0, we can simplify the equation to:
v=0+(1.25m/s2)×(6.0s)
Calculating the final velocity:
v=1.25×6.0=7.5m/s
Step 4: Conclusion
The speed of the box at the end of the 6.0 s interval is 7.5 m/s.
---
- Net force (F) = 15 N
- Mass of the box (m) = 12 kg
- Initial velocity (u) = 0 m/s (the box is initially at rest)
- Time (t) = 6.0 s
According to Newton's second law of motion, the net force acting on an object is equal to the mass of the object multiplied by its acceleration (F = m * a). We can rearrange this formula to find the acceleration (a):
The first equation of motion relates initial velocity (u), final velocity (v), acceleration (a), and time (t):
The speed of the box at the end of the 6.0 s interval is 7.5 m/s.
Topper's Solved these Questions
- FORCE AND MOTION - I Book:RESNICK AND HALLIDAYChapter:FORCE AND MOTION - I Exercise:PRACTICE QUESTIONS (More than One Correct Choice Type)
Explore 5 Videos
- FORCE AND MOTION - I Book:RESNICK AND HALLIDAYChapter:FORCE AND MOTION - I Exercise:PRACTICE QUESTIONS (Linked Comprehension)
Explore 10 Videos
- FORCE AND MOTION - I Book:RESNICK AND HALLIDAYChapter:FORCE AND MOTION - I Exercise:PROBLEMS
Explore 52 Videos
- FLUIDSBook:RESNICK AND HALLIDAYChapter:FLUIDSExercise:PRACTICE QUESTIONS (Integer Type )
Explore 5 Videos
- FORCE AND MOTION-IIBook:RESNICK AND HALLIDAYChapter:FORCE AND MOTION-IIExercise:PRACTICE QUESTIONS (Integer Type)
Explore 1 Video
Similar Questions
A force F=2t2 is applied to the cart initially at rest. The speed of the cart at t = 5 s is -
View SolutionA force of 5.0 N acts on a 15 kg body initially at rest. Compute the work done by the force in (a) the first, (b) the second, and (c) the third seconds and (d) the instantaneous power due to the force at the end of the third second.
View Solution
Knowledge Check
A constant retarding force of 50 N is applied to a body of mass 10kg moving initially with a speed of 10 ms−1. The body comes to rest after
A2 secondB4 secondC6 secondD8 secondA constant retarding force of 80 N is applied to a body of mass 50 kg which is moving initially with a speed of 20 m/s. What would be the time required by the body to come to rest ?
A15 sB14 sC12.5 sD18 sA constant retarding force of 80 N is applied to a body of mass 50 kg which is moving initially with a speed of 20 m/s. What would be the time required by the body to come to rest ?
A15sB14sC12.5sD18s
A box of bananas weighing 40.0Nrests on a horizontal surface is 0.40 and the coefficient of kinetic friction is 0.20
a. If no horizontal force is applied to the box and the box is at rest , how large is the friction force excered on the box ?
b. What is the magnitude of the friction forces if a monkey applies a horizontal force of 6.0N to the box and the box is initial at rest?
c. What minimum horizontal force must the monkey apply to start the box in motion ?
d. What minimum horizontal force must the monkey apply to keep the box moving at constant velocity once it has been starts?
e. If the monkey applies a horizontal force of 18.0N What is the magnitude of the friction force and what is the box's acceleration ?
View SolutionA 50.0-kg boy runs at a speed of 10.0 m/s and jumps onto a cart as shown in the figure. The cart is initially at rest. If the speed of the cart with the boy on it is 2.50 m/s, what is the mass of the cart?

View SolutionCalculate the kinetic energy acquired by a body of mass 5 kg initially at rest , when subjected to a force of 20 N , at the end of 8 s .
View SolutionA body of mass 5 kg initially at rest is subject to a force of 20 N. What is the kinetic energy acquired by the body at the end of 10 s ?
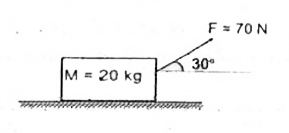
View SolutionA wooden box of mass 20 kg is kept on a rough horizontal surface. The co-efficient of static friction μs=0.41 and co-efficient of kinetic friction μk=0.3 exist between the box and the horizontal surface. A constant force F of 70N is applied to the box at an angle of 30∘ with the horizontal. Find the acceleration of the box on the surface and the frictional force on the box. Take g=10m/s2.
View Solution

