A force of 5.0 N acts on a 15 kg body initially at rest. Compute the work done by the force in (a) the first, (b) the second, and (c) the third seconds and (d) the instantaneous power due to the force at the end of the third second.
The correct Answer is:(a) 0.83 J; (b) 2.5 J; (c) 4.2 J ; (d) 5.0 W
To solve the problem step by step, we will break it down into parts (a), (b), (c), and (d) as requested.
Given:
- Force (F) = 5.0 N
- Mass (m) = 15 kg
- Initial velocity (u) = 0 m/s (body is initially at rest)
Step 1: Calculate the acceleration.
Using Newton's second law, we can find the acceleration (a) using the formula:
a=Fm
Substituting the values:
a=5.0N15kg=13m/s2
Step 2: Calculate the work done in the first second (part a).
The displacement (s) in the first second can be calculated using the formula:
s=ut+12at2
Since the initial velocity (u) is 0:
s=0+12(13)(12)=16m
Now, work done (W) is given by:
W=F⋅s
Substituting the values:
W=5.0N⋅16m=56J≈0.83J
Step 3: Calculate the work done in the second second (part b).
For the second second, we can use the formula for displacement during the nth second:
sn=u+a2(2n−1)
Substituting n=2:
s2=0+12(13)(2⋅2−1)=12(13)(3)=12m
Now, calculate the work done:
W=F⋅s2=5.0N⋅12m=2.5J
Step 4: Calculate the work done in the third second (part c).
For the third second, using the same formula:
s3=u+a2(2n−1)
Substituting n=3:
s3=0+12(13)(2⋅3−1)=12(13)(5)=56m
Now, calculate the work done:
W=F⋅s3=5.0N⋅56m=256J≈4.17J
Step 5: Calculate the instantaneous power at the end of the third second (part d).
First, we need to find the final velocity (v) at the end of the third second using:
v=u+at
Substituting t=3:
v=0+(13)(3)=1m/s
Now, the instantaneous power (P) is given by:
P=F⋅v
Substituting the values:
P=5.0N⋅1m/s=5W
Final Answers:
(a) Work done in the first second: ≈0.83J
(b) Work done in the second second: 2.5J
(c) Work done in the third second: ≈4.17J
(d) Instantaneous power at the end of the third second: 5W
- Force (F) = 5.0 N
- Mass (m) = 15 kg
- Initial velocity (u) = 0 m/s (body is initially at rest)
Using Newton's second law, we can find the acceleration (a) using the formula:
a=Fm
a=5.0N15kg=13m/s2
The displacement (s) in the first second can be calculated using the formula:
s=ut+12at2
Since the initial velocity (u) is 0:
s=0+12(13)(12)=16m
W=F⋅s
Substituting the values:
W=5.0N⋅16m=56J≈0.83J
For the second second, we can use the formula for displacement during the nth second:
sn=u+a2(2n−1)
Substituting n=2:
s2=0+12(13)(2⋅2−1)=12(13)(3)=12m
W=F⋅s2=5.0N⋅12m=2.5J
For the third second, using the same formula:
s3=u+a2(2n−1)
Substituting n=3:
s3=0+12(13)(2⋅3−1)=12(13)(5)=56m
W=F⋅s3=5.0N⋅56m=256J≈4.17J
First, we need to find the final velocity (v) at the end of the third second using:
v=u+at
Substituting t=3:
v=0+(13)(3)=1m/s
P=F⋅v
Substituting the values:
P=5.0N⋅1m/s=5W
(a) Work done in the first second: ≈0.83J
(b) Work done in the second second: 2.5J
(c) Work done in the third second: ≈4.17J
(d) Instantaneous power at the end of the third second: 5W
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:PRACTICE QUESTIONS (Single Correct Choice Type)
Explore 59 Videos
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:PRACTICE QUESTIONS (More than one choice correct type)
Explore 10 Videos
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:CHECKPOINT
Explore 6 Videos
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Practice Questions (Integer Type)
Explore 4 Videos
Similar Questions
A force of 2N acts for 5seconds on a particle of mass 0.5kg initially at rest. Calculate the distance moved by the particle in (i) these five seconds and (ii) next 5seconds
View SolutionA block of mass 2.0 kg is pushed down an inclined plane of inclination 370 with a force of 20N cting parallelto the incline. It is found tht the block moves on the incline with an acceleration of 10ms2. If the blcok started from rest, find the work done a. by the applied force in the first second b. by the weight of the block in the first second and c. by the frictional force acting on the block in the first second. Take g=10ms2.
View Solution
Knowledge Check
A force of 5 N acts on a 15 kg body initially at rest. The work done by the force during the first second of motion of the body is
A5 JB56JC6JD75 JA force of 5 N acts on a 15 kg body initially at rest. The work done by the force during the first second of motion of the body is
A5JB56JC6JD75JA force given by the relation F = 8t, acts on a body of mass 2 kg, initially at rest. Find the work done by this force on the body during first 2 seconds of its motion
A64 JBzeroC−64JDnone of these
" The distances traveled by a body falling freely from rest in the first,second and third seconds are in the ratio "
View SolutionA variable force acts on a body of mass 2 kg initially at rest as shown in figure . Calculate the impulse of the force in first 2 seconds and speed of the body after 2 seconds .
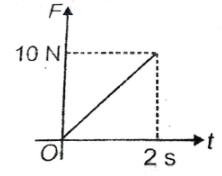
View SolutionA force acts on a 2 kg object so that its position is given as a function of time as x=3t2+5. What is the work done by this force in first 5 seconds ?
View SolutionA force given by the relation F=8t, acts on a body of mass 2kg, initialiy at rest. Find the work done by this force on the body during first 2 seconds of its motion.
View SolutionIf a body of mass 5 kg initially at rest is acted upon by a force of 50 dyne for 3s, then the impulse will be
View Solution

