Two bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
(M−m)g
mg
2 mg
(m/M)mg
The correct Answer is:C
To find the tension in the string when two bodies of masses m and M are attached to either end of a light string passing over a fixed ideal pulley, we can follow these steps:
1. Identify the Forces Acting on Each Mass:
- For mass M (the larger mass), the forces acting on it are:
- Weight: Mg (downward)
- Tension: T (upward)
- For mass m (the smaller mass), the forces acting on it are:
- Weight: mg (downward)
- Tension: T (upward)
2. Apply Newton's Second Law:
- For mass M (going down), the equation of motion can be written as:
Mg−T=Ma(1)
- For mass m (going up), the equation of motion can be written as:
T−mg=ma(2)
3. Express Acceleration a:
- From equation (1):
T=Mg−Ma(3)
- From equation (2):
T=ma+mg(4)
4. Set Equations for Tension Equal:
- Set equations (3) and (4) equal to each other:
Mg−Ma=ma+mg
5. Rearrange to Solve for Acceleration a:
- Rearranging gives:
Mg−mg=Ma+ma
- Factor out a:
Mg−mg=a(M+m)
- Therefore, the acceleration a is:
a=(M−m)gM+m(5)
6. Substitute a Back to Find Tension T:
- Substitute a from equation (5) into either equation (3) or (4). Using equation (3):
T=Mg−M((M−m)gM+m)
- Simplifying gives:
T=Mg−M(M−m)gM+m
- Combine terms:
T=Mg(M+m)−M(M−m)gM+m
- This simplifies to:
T=(Mg2+mgM)−(M2g−mgM)M+m
- Further simplification leads to:
T≈2mg1(for M≫m)
7. Final Result:
- Thus, the tension in the string is approximately:
T≈2mg
- For mass M (the larger mass), the forces acting on it are:
- Weight: Mg (downward)
- Tension: T (upward)
- For mass m (the smaller mass), the forces acting on it are:
- Weight: mg (downward)
- Tension: T (upward)
- For mass M (going down), the equation of motion can be written as:
Mg−T=Ma(1)
- For mass m (going up), the equation of motion can be written as:
T−mg=ma(2)
- From equation (1):
T=Mg−Ma(3)
- From equation (2):
T=ma+mg(4)
- Set equations (3) and (4) equal to each other:
Mg−Ma=ma+mg
- Rearranging gives:
Mg−mg=Ma+ma
- Factor out a:
Mg−mg=a(M+m)
- Therefore, the acceleration a is:
a=(M−m)gM+m(5)
- Substitute a from equation (5) into either equation (3) or (4). Using equation (3):
T=Mg−M((M−m)gM+m)
- Simplifying gives:
T=Mg−M(M−m)gM+m
- Combine terms:
T=Mg(M+m)−M(M−m)gM+m
- This simplifies to:
T=(Mg2+mgM)−(M2g−mgM)M+m
- Further simplification leads to:
T≈2mg1(for M≫m)
- Thus, the tension in the string is approximately:
T≈2mg
Topper's Solved these Questions
- FORCE AND MOTION - I Book:RESNICK AND HALLIDAYChapter:FORCE AND MOTION - I Exercise:PRACTICE QUESTIONS (More than One Correct Choice Type)
Explore 5 Videos
- FORCE AND MOTION - I Book:RESNICK AND HALLIDAYChapter:FORCE AND MOTION - I Exercise:PRACTICE QUESTIONS (Linked Comprehension)
Explore 10 Videos
- FORCE AND MOTION - I Book:RESNICK AND HALLIDAYChapter:FORCE AND MOTION - I Exercise:PROBLEMS
Explore 52 Videos
- FLUIDSBook:RESNICK AND HALLIDAYChapter:FLUIDSExercise:PRACTICE QUESTIONS (Integer Type )
Explore 5 Videos
- FORCE AND MOTION-IIBook:RESNICK AND HALLIDAYChapter:FORCE AND MOTION-IIExercise:PRACTICE QUESTIONS (Integer Type)
Explore 1 Video
Similar Questions
Two bodies of masses 4kg and 3kg respectively are connected by a light string passing over a smooth frictionless pulley Calculate the acceleration of the masses and tension in the string .
View SolutionTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)

View Solution
Knowledge Check
Two bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
A(M−m)gBmgC2mgD(m/M)mgTwo bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
A(m−m)gBmgC2mgD(mM)mgTwo bodies of mass 4kg and 6kg are attached to the ends of a string passing over a pulley. The 4kg mass is attached to the table top by another string. The tension in this string T1 is equal to: Take
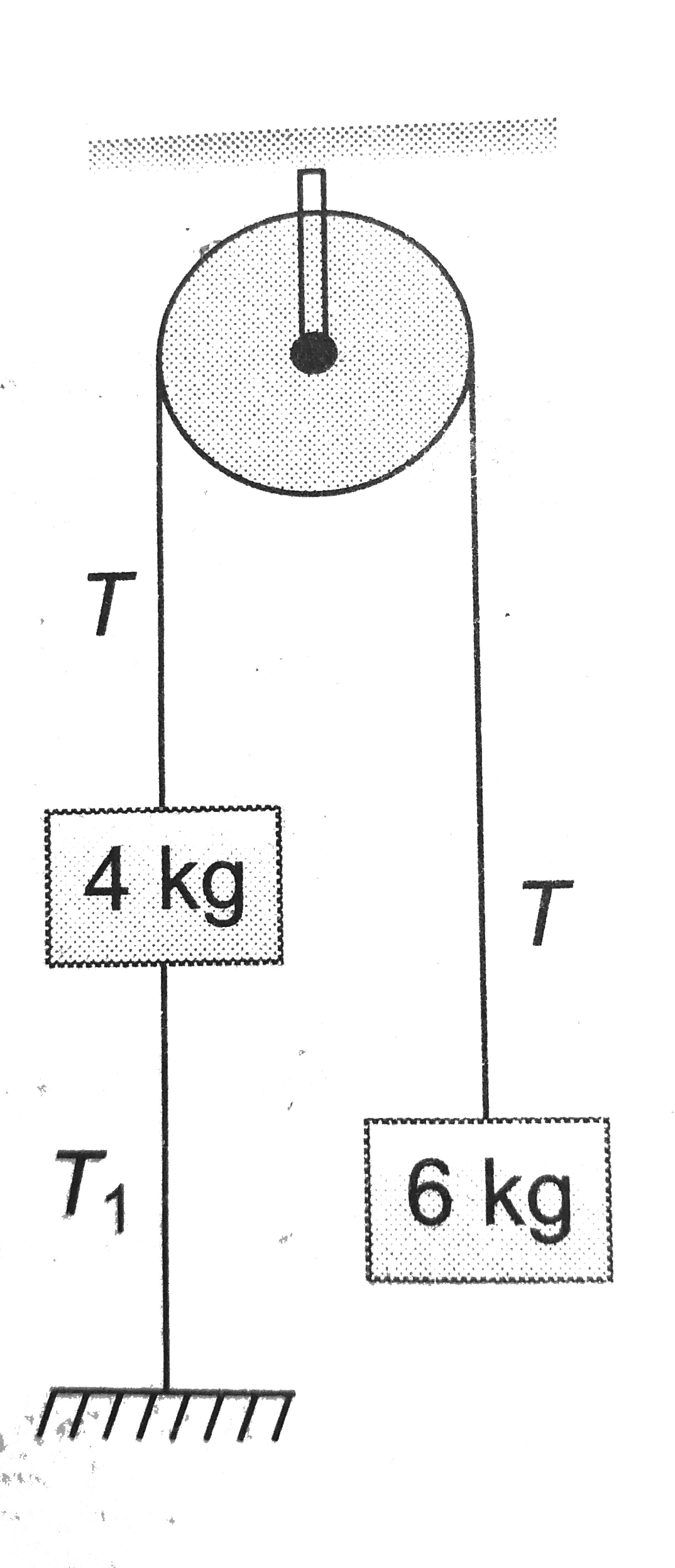 A20NB25NC10.6ND10N
A20NB25NC10.6ND10N
Two bodies of masses 4kg and 6kg are attached to the ends of a string which passes over a pulley, the 4kg mass is attached to the table top by another string.The tension in this string T1 is equal to
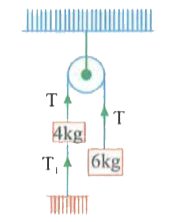
View SolutionTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View SolutionTwo masses M and m(M>m) are joined by a light string passing over a smooth light pulley.

View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo weights w1 and w2 are suspended from the ends of a light string passing over a smooth fixed pulley. If the pulley is pulled up at an acceleration g , the tension in the string will be
View Solution

