Question

In $a\Delta ABC,AD$ is a median and $AL\perp BC$.
Prove that
(a) $A{C}^2=A{D}^2+BC\cdot DL+{\left(\frac{BC}{2}\right)}^2$
(b) $A{B}^2=A{D}^2-BC\cdot DL+{\left(\frac{BC}{2}\right)}^2$
(c) $A{C}^2+A{B}^2=2A{D}^2=2A{D}^2+\frac{1}{2}B{C}^2$

Explanation

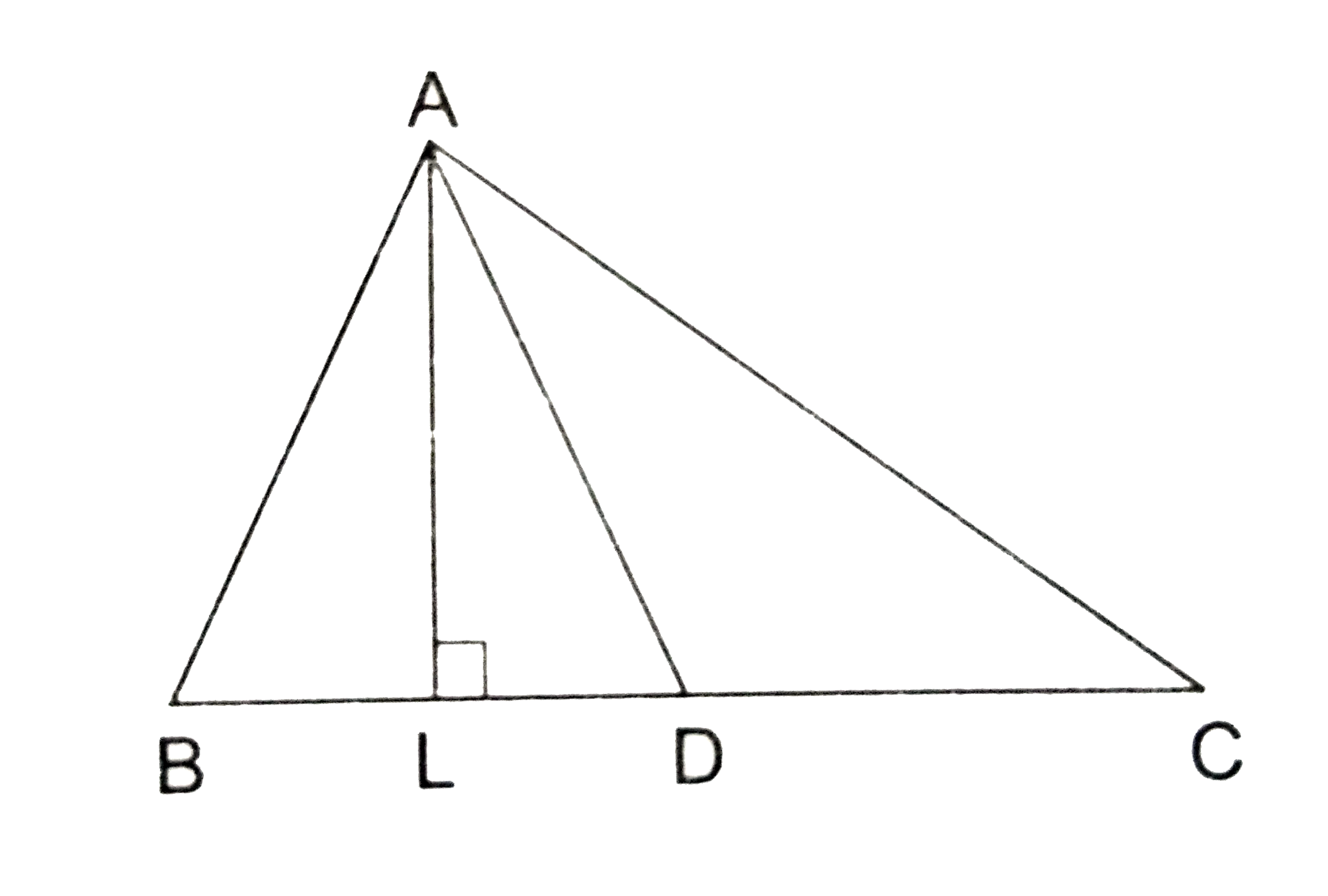
In right `Delta ACL, AC^(2)=AL^(2)+LC^(2)" ".....(i)`
In right `Delta ALD, AL^(2)=AD^(2)-DL^(2)" ".....(ii)`
`:. AC^(2)=(AD^(2)-DL^(2))+LC^(2)` [ from (i) and (ii) ]
`=(AD^(2)-DL^(2))+(DL+DC)^(2)`
`=(AD^(2)-DL^(2))+(DL+(1)/(2)BC)^(2)`
`=AD^(2)+BC*DL+(1)/(4)BC^(2)=AD^(2)+BC*DL+((BC)/(2))^(2)`

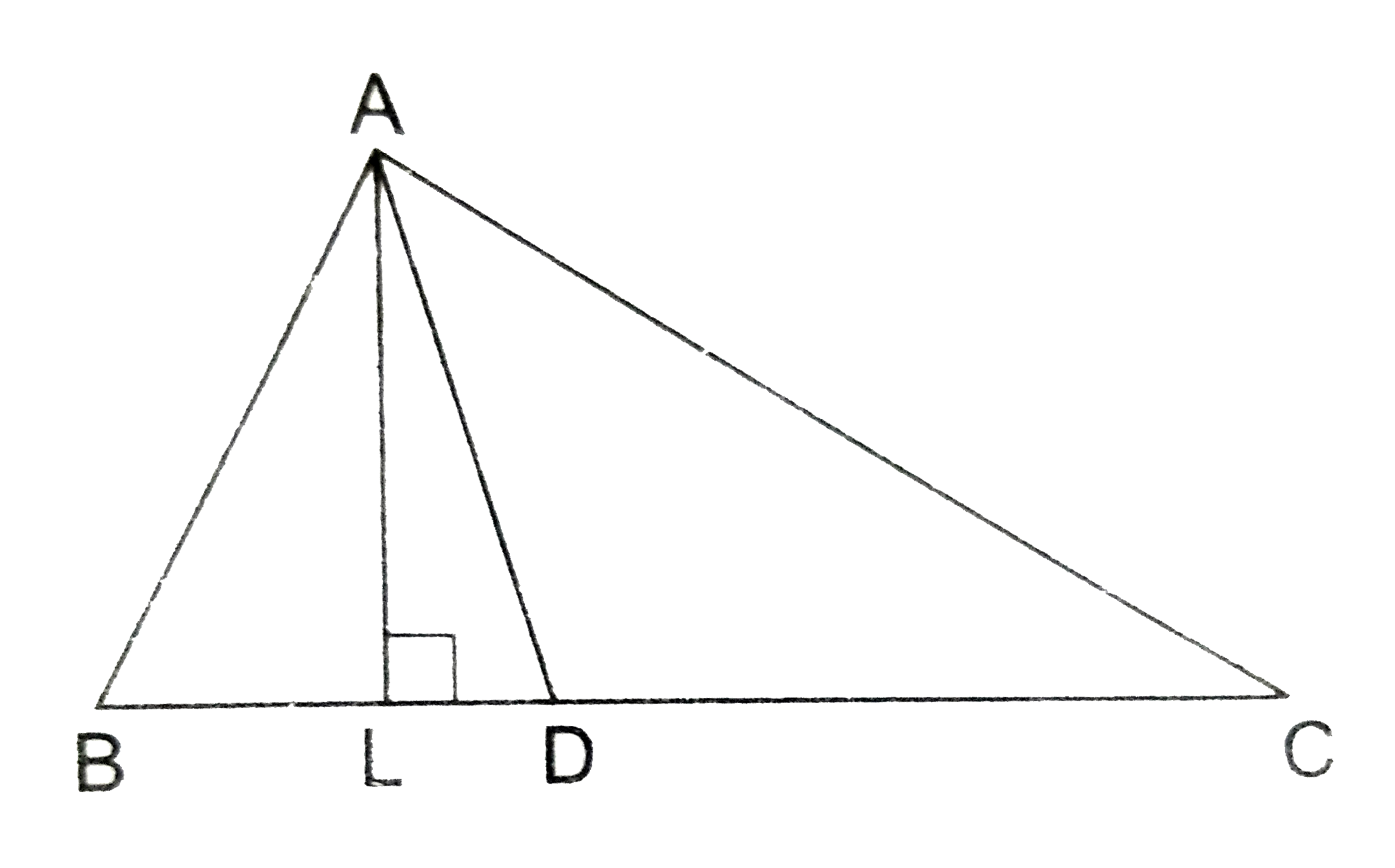
(b) In right `Delta ABL, AB^(2)=AL^(2)+LB^(2)" ".....(iii)`
In right `Delta ALD, AL^(2)=AD^(2)-DL^(2)" ".....(iv)`
`:. AB^(2)=(AD^(2)-DL^(2))+LB^(2)` [ from (iii) and (iv) ]
`=(AD^(2)-DL^(2))+(BD-DL)^(2)`
`=(AD^(2)-DL^(2))+((1)/(2)BC-DL)^(2)=AD^(2)-BC*DL+((BC)/(2))^(2)`
(c) Adding the results of (a) and (b), we get
`AC^(2)+AB^(2)=2AD^(2)+(1)/(2)BC^(2)`.