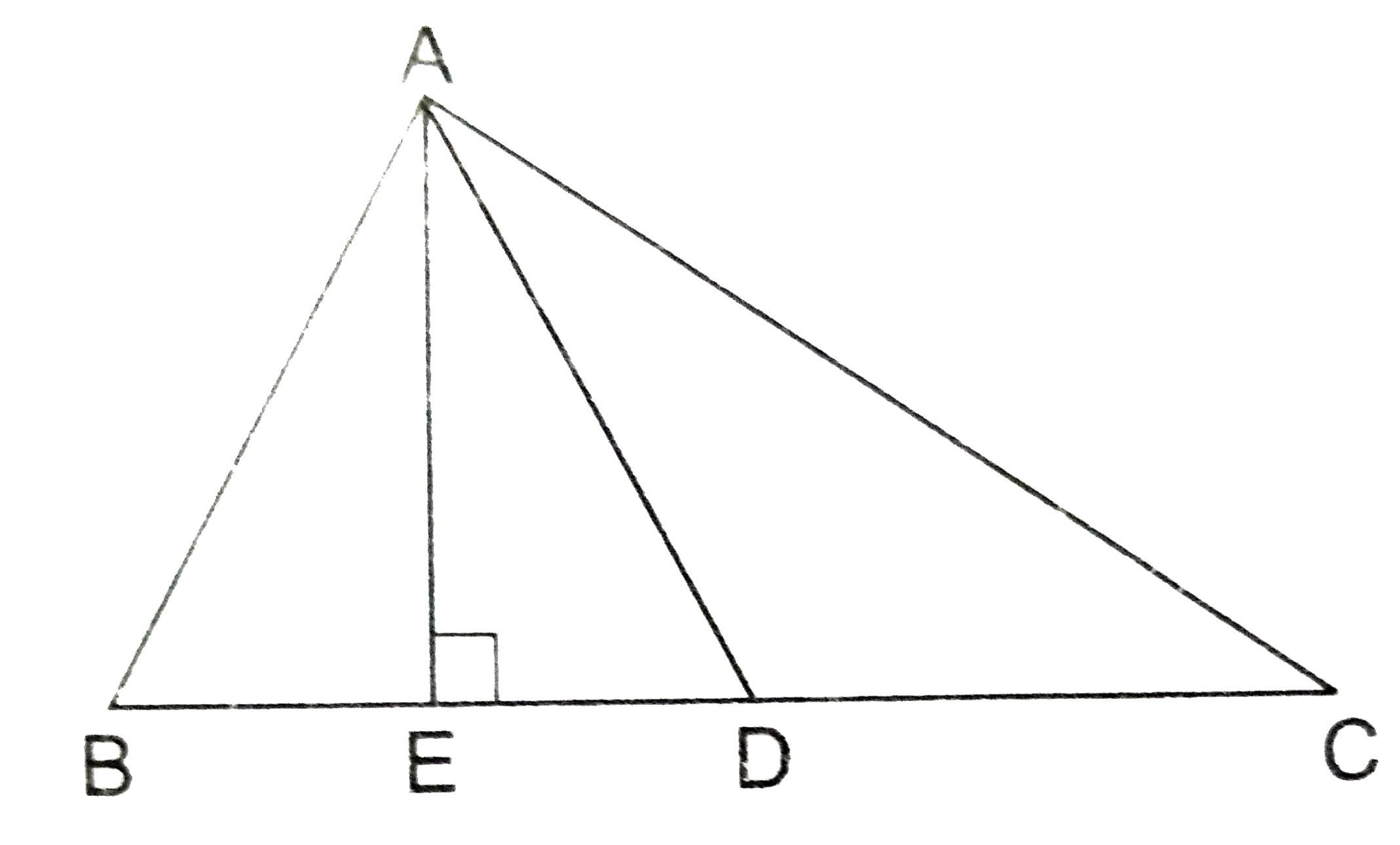
In ΔABC,D is the midpoint of BC and AE⊥BC. If AC>AB, show that AB2=AD2−BC⋅DE+14BC2
In ΔAFB,∠AEB=90∘
∴AB2=AE2+BE2 ...(i)
In ΔAED,∠AED=90∘
∴AD2=(AE2+DE2)
⇒AE2=(AD2−DE2)
∴AB2=(AD2−DE2)+BE2 [ using (i)] ltbr? =(AD2−DE2)+(BD−DE)2
=(AD2−DE2)+(12BC−DE)2
=AD2+14BC2−BC⋅DE.
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7E
Explore 30 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Multiple Choice Questions (Mcq)
Explore 53 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7C
Explore 13 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
In a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BCDE+14BC2 (ii) AB2+AC2=2 AD2+12BC2
View SolutionIn a triangle ABC, D is midpoint of side BC. If AC>ABandAE⊥BC, then prove that AB2=AD2−BC.ED+14BC2
View SolutionIn a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BCxDE+14BC2
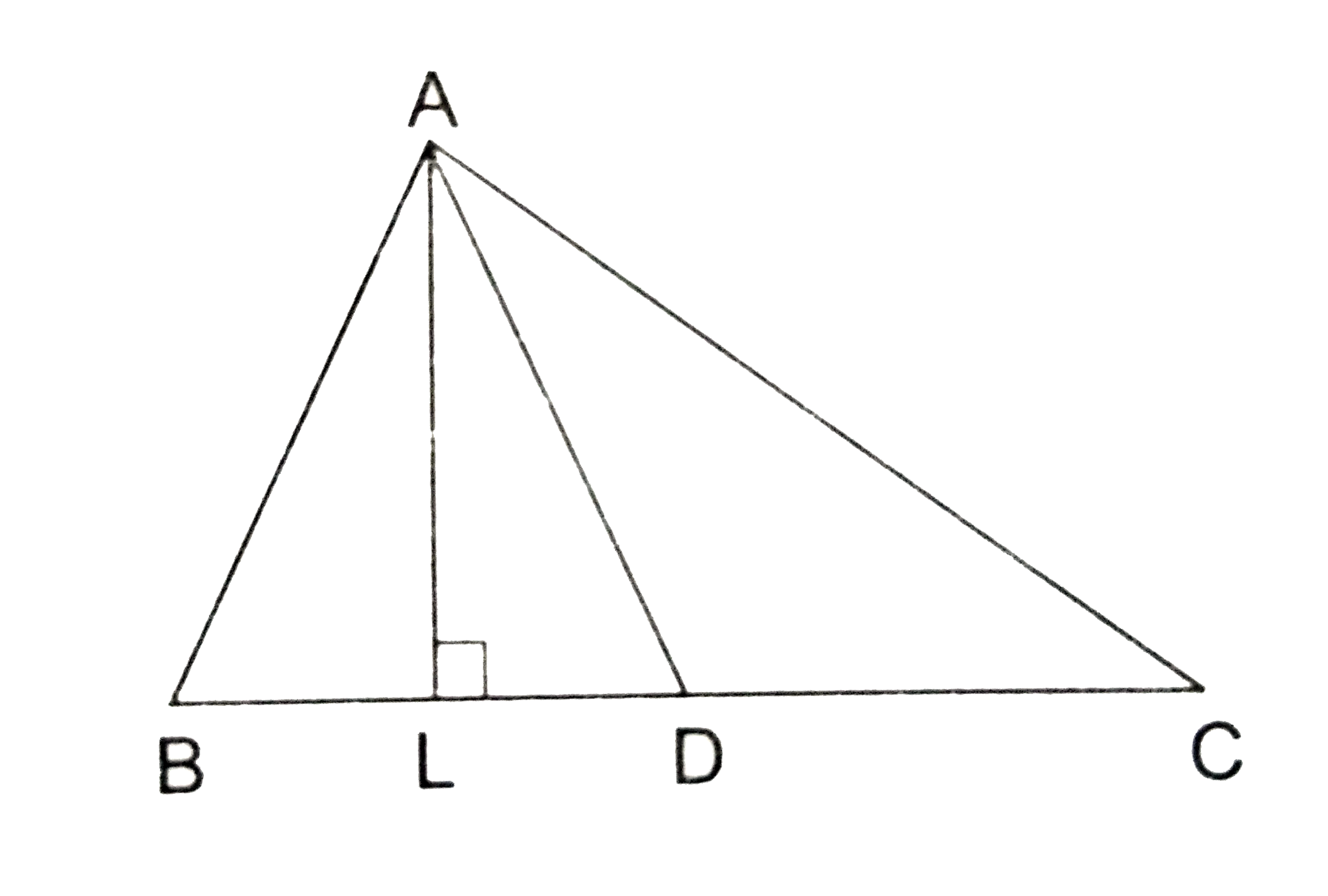
View SolutionIn aΔABC,AD is a median and AL⊥BC.
Prove that
(a) AC2=AD2+BC⋅DL+(BC2)2
(b) AB2=AD2−BC⋅DL+(BC2)2
(c) AC2+AB2=2AD2=2AD2+12BC2
View SolutionABC is a triangle in which AB=AC and D is any point in BC . Prove that AB2−AD2=BDCD .
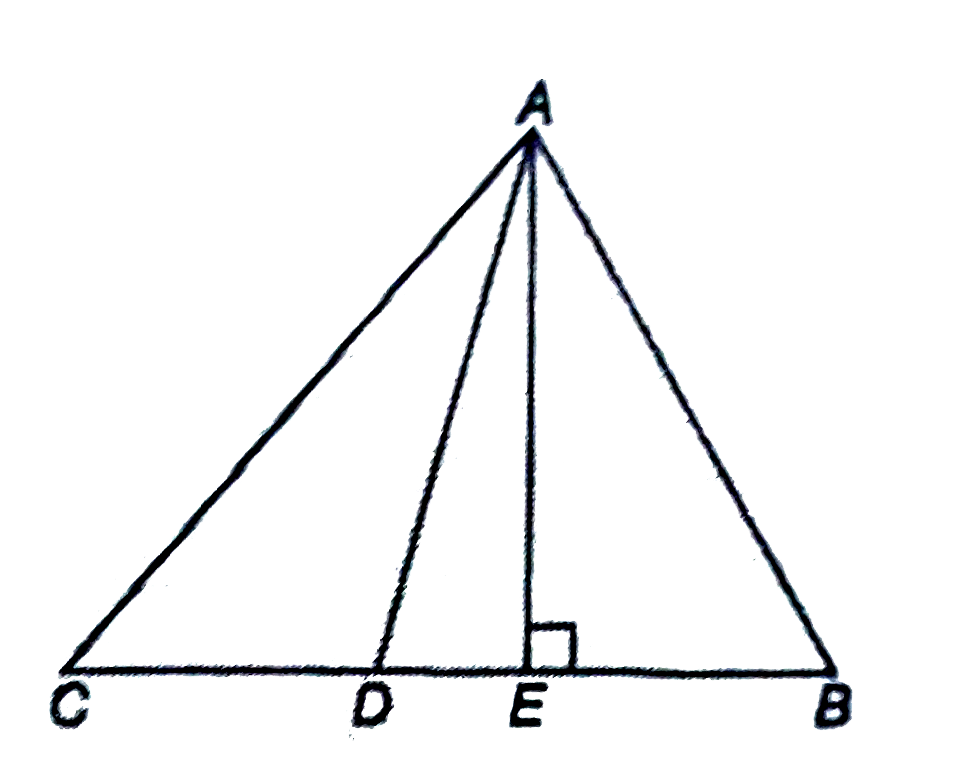
View SolutionThe following figure shows a triangle ABC in which AD is a median and AE⊥BC. Prove that 2AB2+2AC2=4AD2+BC2 .
View SolutionIn ΔABC, if D is any point on the side BC, show that (AB+BC+AC)>2AD.

View SolutionIn a ΔABC,∠B is an acute-angle and AD⊥BC
Prove that :
(i) AC2=AB2+BC2−2BC×BD
(ii) AB2+CD2=AC2+BD2
View SolutionIn a ΔABC, ∠B is an acute-angle and AD⊥BC. Prove that:
AB2+CD2=AC2+BD2
View SolutionD is a point on side BC of ΔABC such that AD=AC. Show that AB>AD.
View Solution

