In the given figure, D is the midpoint of side BC and AE⊥BC. If BC=a,AC=b,AB=c,ED=xAD=pandAE=h prove that
(i)b2=p2+ax+a24
(ii) c2=p2−ax+a24
(iii) (b2+c2)=2p2+12a2
(iv)(b2−c2)=2ax.
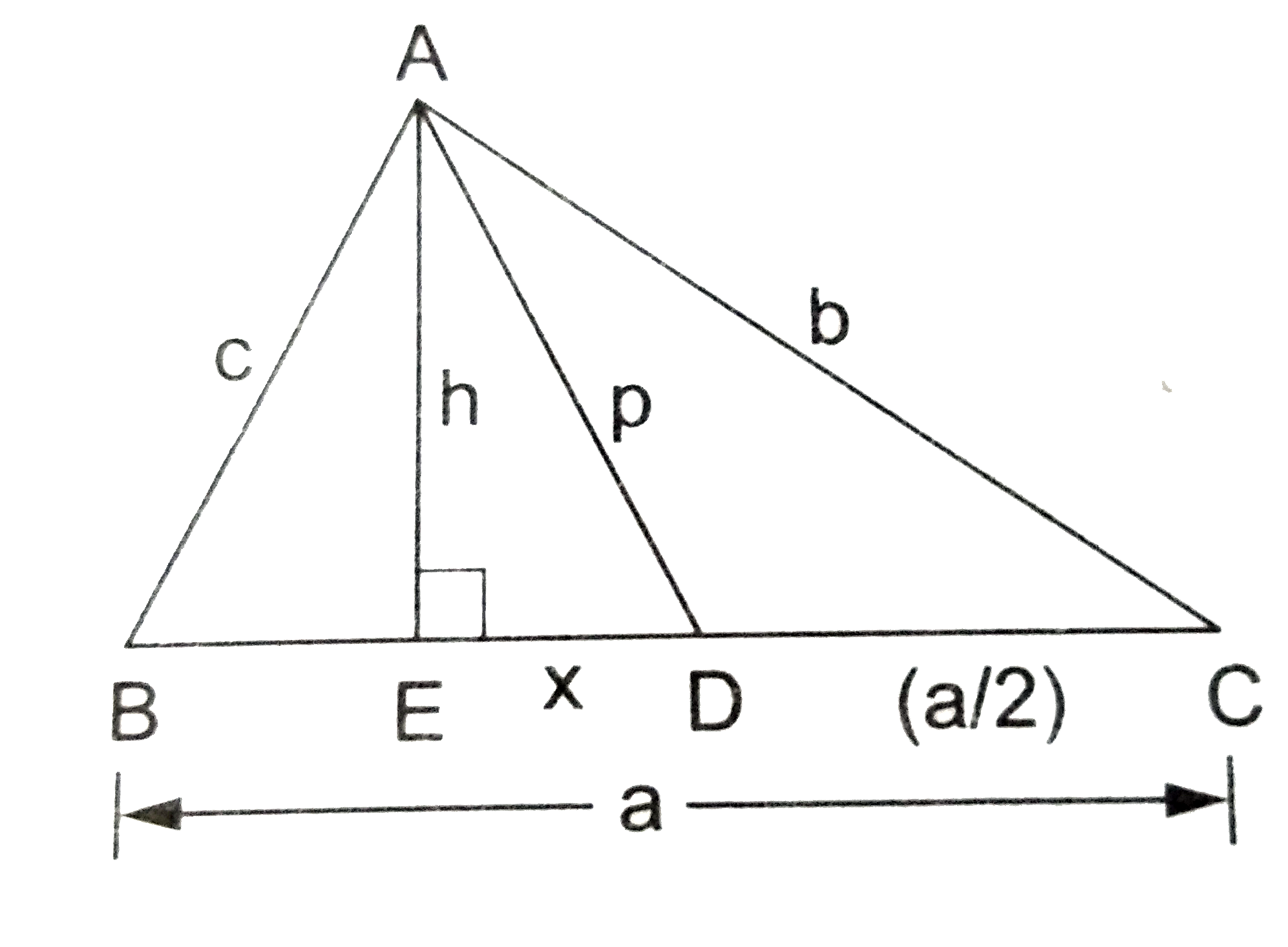
(i)AC2=AE2+EC2
⇒b2=h2+(xa3)2=(h2+x2)+ax+a24
=p2−ax+a24
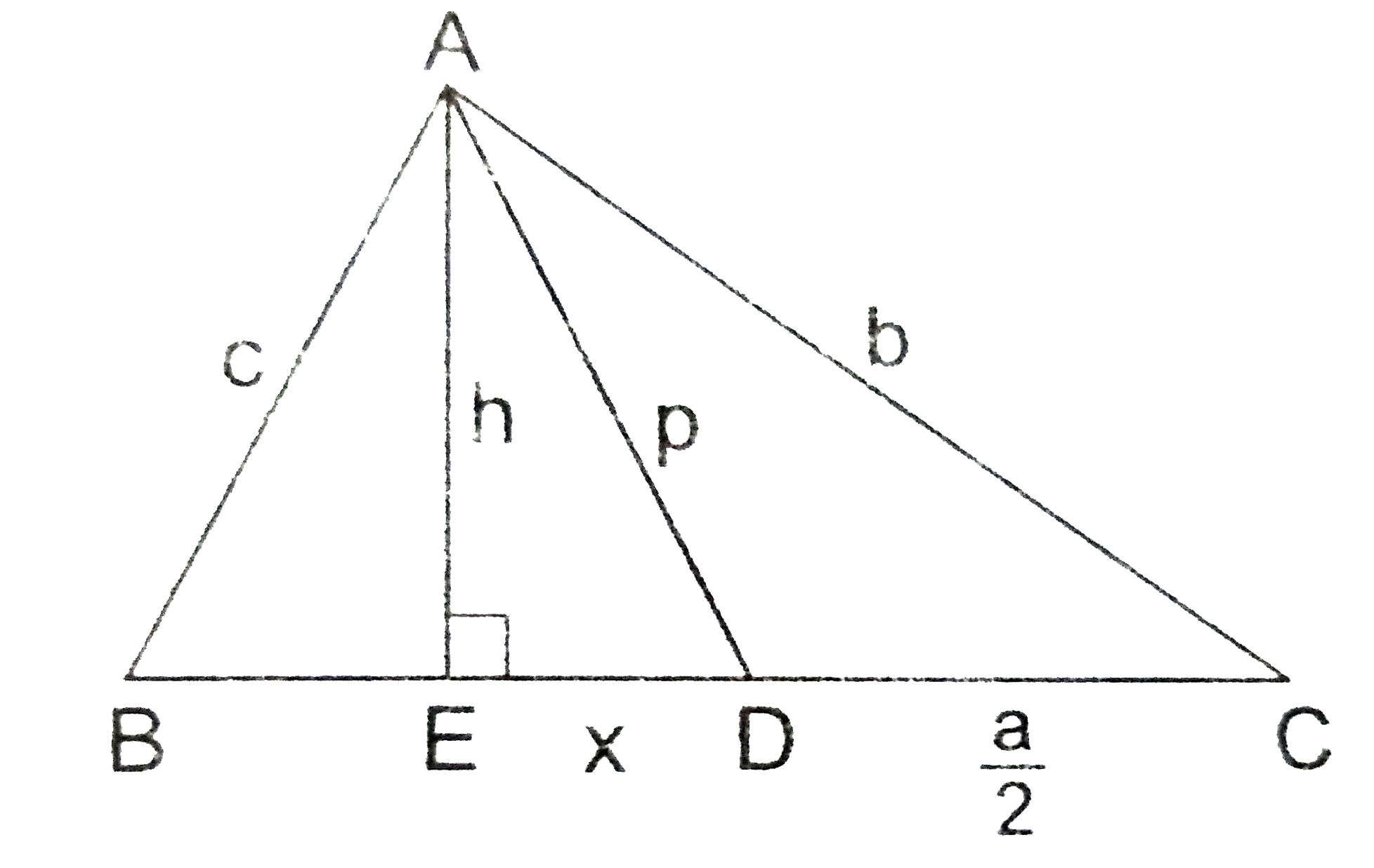
(ii)AB2=AE2+BE2
⇒c2=h2+(a2−x)2=(h2+x2)−ax+a24
=p2−ax+a24
(iii) and (i) and (ii).
(iv) Subtract (ii) from (ii).
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7E
Explore 30 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Multiple Choice Questions (Mcq)
Explore 53 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7C
Explore 13 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
In Fig. 4.220, D is the mid-point of side BC and AE⊥BC . If BC=a, AC=b, AB=c, ED=x, AD=p and AE=p and AE=h , prove that: (FIGURE) b2=p2+ax+a24 (ii) c2=p2−ax+a24 (iii) b2+c2=2 p2+a22
View SolutionIf a, b, c are in A.P., then prove that :
(i)ab+bc=2b2
(ii) (a−c)2=4(b2−ac)
(iii) a2+c2+4ca=2(ab+bc+ca).
View SolutionIn ΔABC,D is the midpoint of BC and AE⊥BC. If AC>AB, show that AB2=AD2−BC⋅DE+14BC2
View SolutionIf a,b,c, d are in G.P., prove that:
(i) (a2−b2), (b2−c2), (c2−d2) are in G.P.
(i) 1a2+b2, 1b2+c2, 1c2+d2 are in G.P.
View SolutionIn a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BCDE+14BC2 (ii) AB2+AC2=2 AD2+12BC2
View Solution(a+b+c)(a2+b2+c2−ab−bc−ac)
View SolutionIn a triangle ABC, D is midpoint of side BC. If AC>ABandAE⊥BC, then prove that AB2=AD2−BC.ED+14BC2
View SolutionIf a, b, c and d are in G.P. show that (a2+b2+c2)(b2+c2+d2)=(ab+bc+cd)2.
View SolutionIf a,b,c are in G.P. , prove that the following are also in G.P,
(i) a2,b2,c2
(ii)a3,b3,c3
(iii) a2+b2,ab+bc,b2+c2
View SolutionIf a2−bca2+bc+b2−acb2+ac+c2−abc2+ab=1 then find a2a2+bc+b2b2+ac+c2c2+ab=?
View Solution

