In an isoscles ΔABC,AB=ACandD is a point on BC. Prove that AB2−AD2=BD⋅CD.
GIVEN AΔABC in which AB=ACandD is point on BC.
TO PROOVE (AB2−AD2)=BD⋅CD.
CONSTRUCTION Draw AL⊥BC.
PROOF In right ΔALBandALC, we have :
hyp. AB= hyp. AC (given)
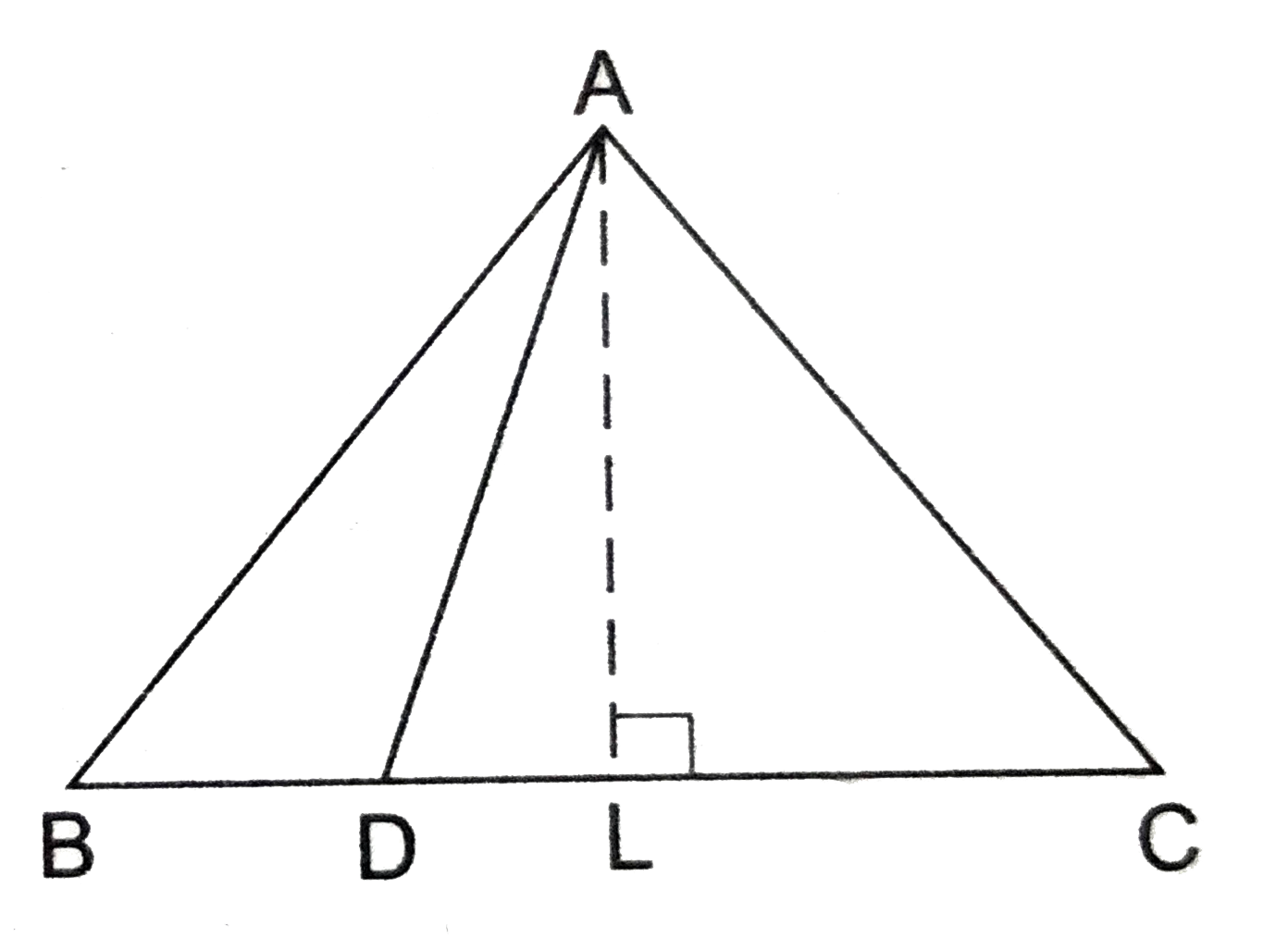
AL=AL ( common)
∴ΔALB≅ΔALC [ by RHS- congruence]
∴BL=CL
From right ΔALBandALD by Pythagora's theorem, we have:
AB2=AL2+BL2 ....(i)
AD2=AL2+DL2 ....(ii)
∴AB2−AD2=BL2−DL2
=(BL−DL)(BL+DL)
=BD⋅(CL+DL) [∴BL=CL]
=BD⋅(CL+DL) [∴BL−DL=BDBDandBL=CL]
=BD⋅CD
Hence, AB2−AD2=BD⋅CD.
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:SOLVED EXAMPLE
Explore 4 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXERCISE 7 A
Explore 1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
In △ABC, AB=AC and D is any point on BC, prove that AB2−AD2=BD.CD
View SolutionIn △ABC,AB>AC and D is any point on BC. Prove that, AB > AD.
View SolutionABC is a triangle in which AB=AC and D is any point in BC . Prove that AB2−AD2=BDCD .
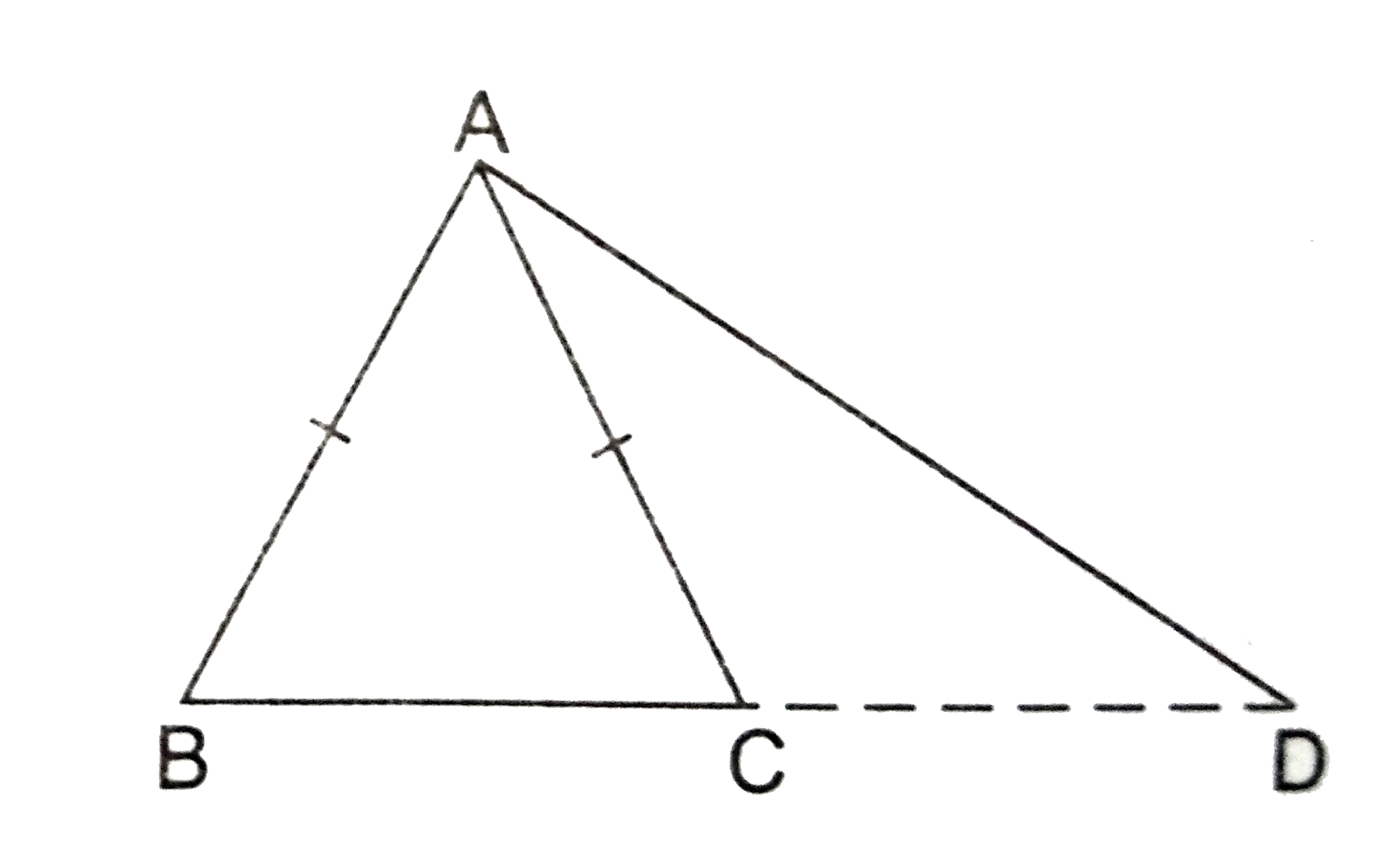
View SolutionIn ΔABC,AB=AC. Side BC is produced to D. Prove that (AD2−AC2)=BD⋅CD.
View SolutionIn ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionIn ΔABC,∠A=90∘,AB=AC,D is any point on BC. Provew that BD2+CD2=2AD2.
View SolutionABC is an isosceles triangle with AB=AC and D is a point on AC such that BC2=ACxCD. Prove that BD=BC
View SolutionIf ABC is an isosceles triangle and D is a point on BC such that AD⊥BC , then AB2−AD2=BD.DC (b) AB2−AD2=BD2−DC2 (c) AB2+AD2=BD.DC (d) AB2+AD2=BD2−DC2
View SolutionIn triangle ABC, ∠A=90∘ , CA= AB and D is a point on AB porduced. Prove that :
DC2−BD2=2AB.AD
View SolutionIn a triangle ABC,B=90∘ and D is the mid-point of BC then prove that AC2=AD2+3CD2
View Solution

