In ΔABC,∠B=35∘,∠C=65∘ and the bisector of ∠BAC meets BC in X. Arrange AX, BX and CX in descending order.
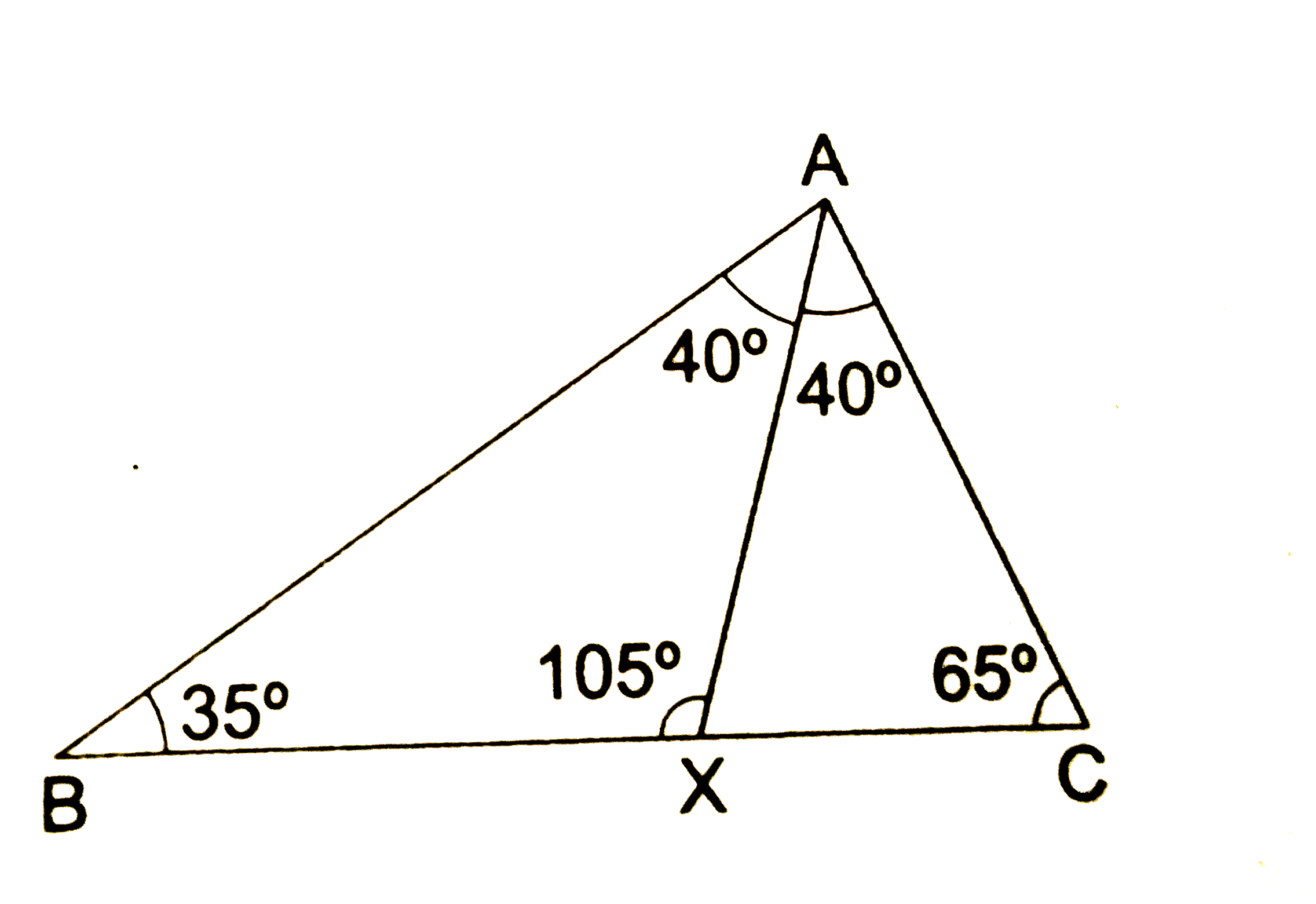
Video Solution
Text Solution
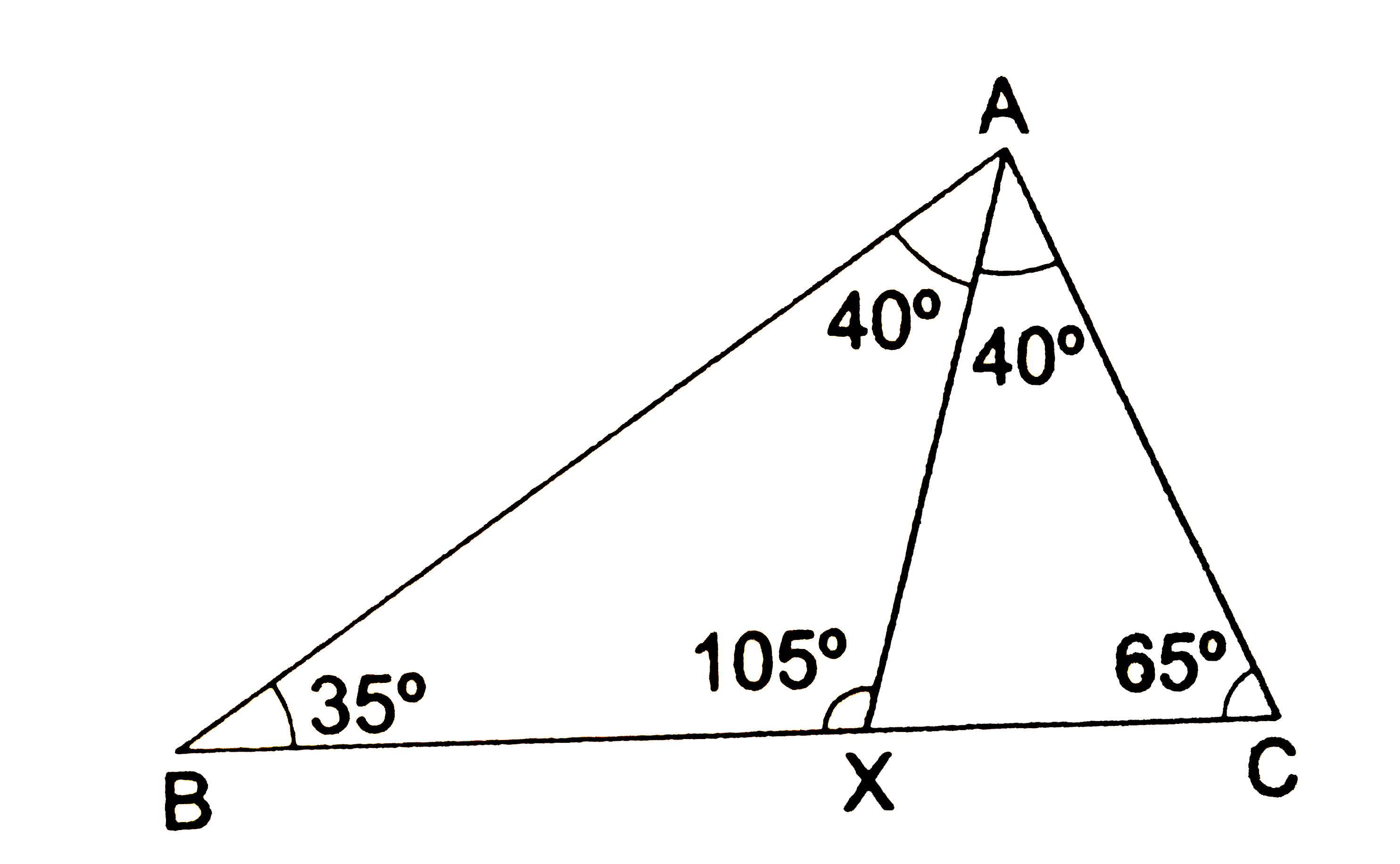
∠A+35∘+65∘=180∘⇒∠A=80∘.
∴ ∠BAX=∠CAX=40∘,∠ABX=35∘,∠ACX=65∘.
∠AXB=180∘−(40∘+35∘)=105∘.
∠BAX>∠ABX⇒BX>AX.
∠ACX>∠CAX⇒AX>CX.
∴ BX>AX>CX.
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
Knowledge Check
In ΔABC,∠B=35∘,∠C=65∘ and the bisector of ∠BAC meets BC in D? Then ∠ADB is :
A40∘B75∘C90∘D105∘In a △ABC,∠A=35∘ and ∠B=65∘,find the measure of ∠C
A80∘B120∘C155∘D140∘In a ΔABC,∠A+∠B=65∘and∠B+∠C=140∘. Find the angles.
A∠A=40∘,∠B=35∘and∠B=35∘and∠C=115∘.B∠A=40∘,∠B=25∘and∠B=25∘and∠C=115∘.C∠A=40∘,∠B=25∘and∠B=25∘and∠C=125∘.D∠A=50∘,∠B=25∘and∠B=25∘and∠C=115∘.
In ΔABC,AD is the bisector of ∠A. Write AB, BD and DC in descending order of their length.

View SolutionIn a ΔABC,∠B=65∘and∠C=80∘, then the longest side is _________.
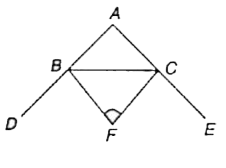
View SolutionIn the given diagram of ΔABC,∠B=80∘,∠C=30∘ BF and CF are the angle bisectors of ∠CBDand∠BCE respectively. Find the value of ∠BFC :
View SolutionIn ΔABC,∠B=55∘ and ∠C=65∘. Then the measure of an exterior angle of ∠A can be .............
View SolutionIn ΔABC,∠A=x+15∘,∠B=xand∠C=2x−35∘ find, each angle of the triangle.
View Solution
