AB and CD are respectively the smallest and largest sides of a quadrilateral ABCD. Show that ∠A>∠Cand∠B>∠C.

Video Solution
Text Solution
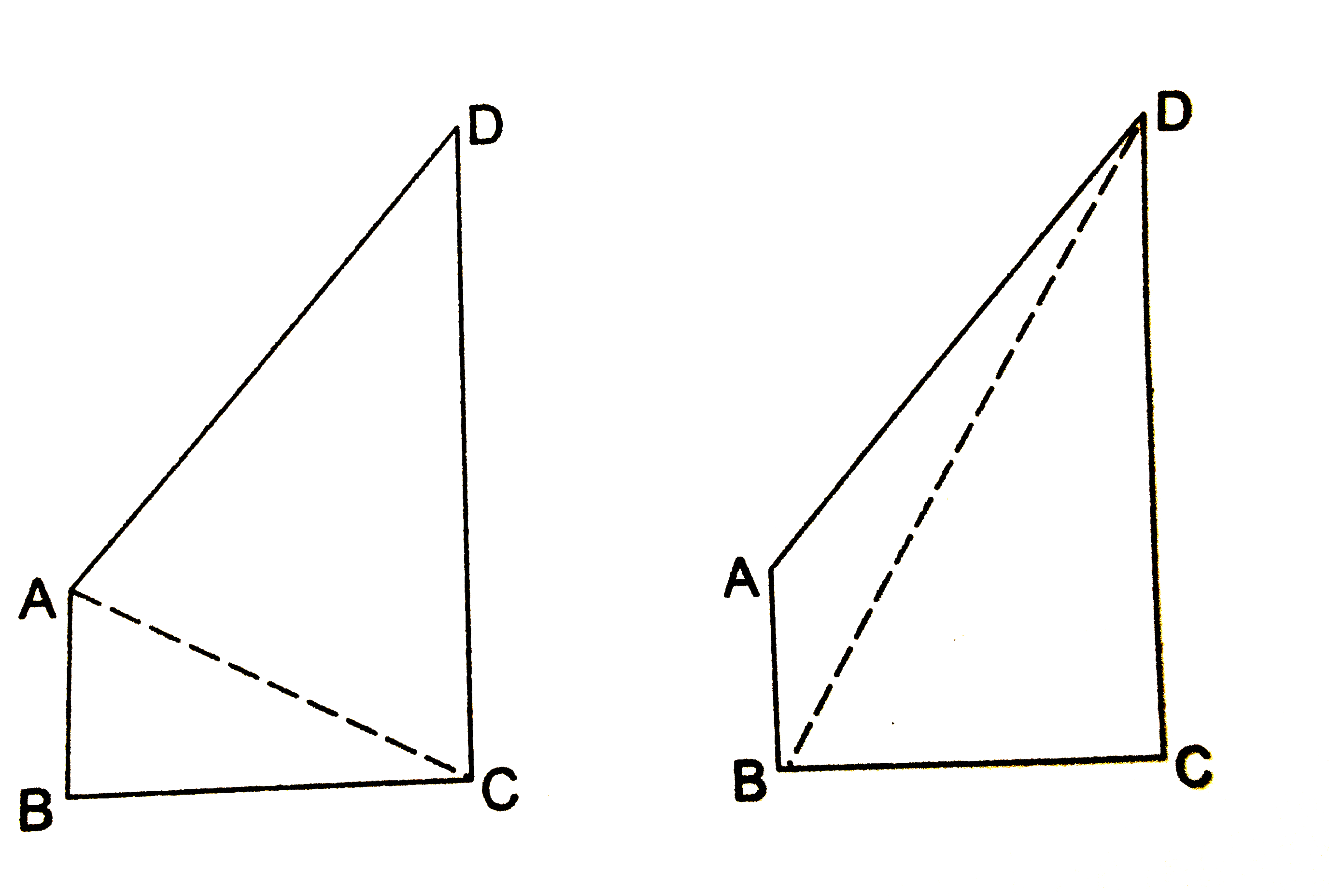
Joint AC. In ΔABC, we have
AB<BC⇒BC>AB
⇒ ∠BAC>∠ACB. …(i)
In ΔACD, we have
CD>AD⇒∠CAD>∠ACD. …(ii)
∴ (∠BAC+∠CAD)>(∠ACB+∠ACD)
⇒ ∠A>∠C.
Similarly, by joining B and D, we may prove that ∠B>∠D.
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
Knowledge Check
In a quadrilateral ABCD,∠A+∠C=180∘, then ∠B+∠D is equal to
A360∘B100∘C180∘D80∘If bisectors of ∠Aand∠B of a quadrilateral ABCD intersect each other at P, of ∠Band∠C at Q, of ∠Cand∠D at R and of ∠Dand∠A at S, then PQRS is a
ArectangleBrhombusCparallelogramDquadrilateral whose opposite angles are supplementary
In □ABCD,AB is the smallest and CD is the largest side. Prove that :
(i) ∠B>∠D (ii) ∠A>∠C
View SolutionABCD is a quadrilateral in which AB||DC and AD = BC. Prove that ∠A=∠Band∠C=∠D.
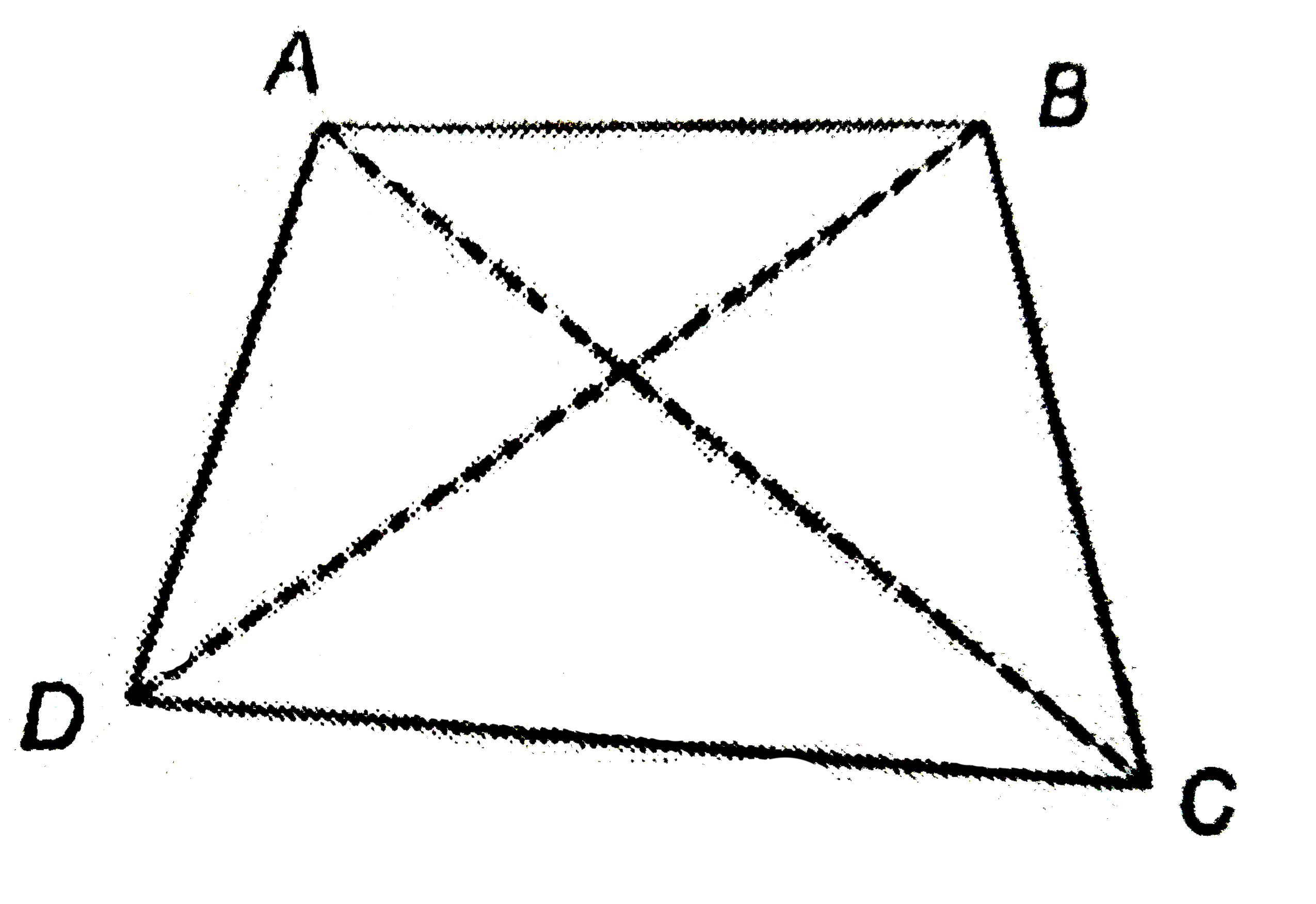
View SolutionIn a quadrilateral ABCD, show that
(AB+BC+CD+DA)>(AC+BD).
View SolutionBisectors of angles A and D of a quadrilateral ABCD meet at P. Prove that ∠APD=12(∠B+∠C)
View SolutionIn quadrilateral ABCD, AB ||CD and AD= BC, prove that ∠A=∠B.
View SolutionThe given figure shows a quadrilateral ABCD. Prove that :
AB+BC+CD+DA>AC+BD

View Solution