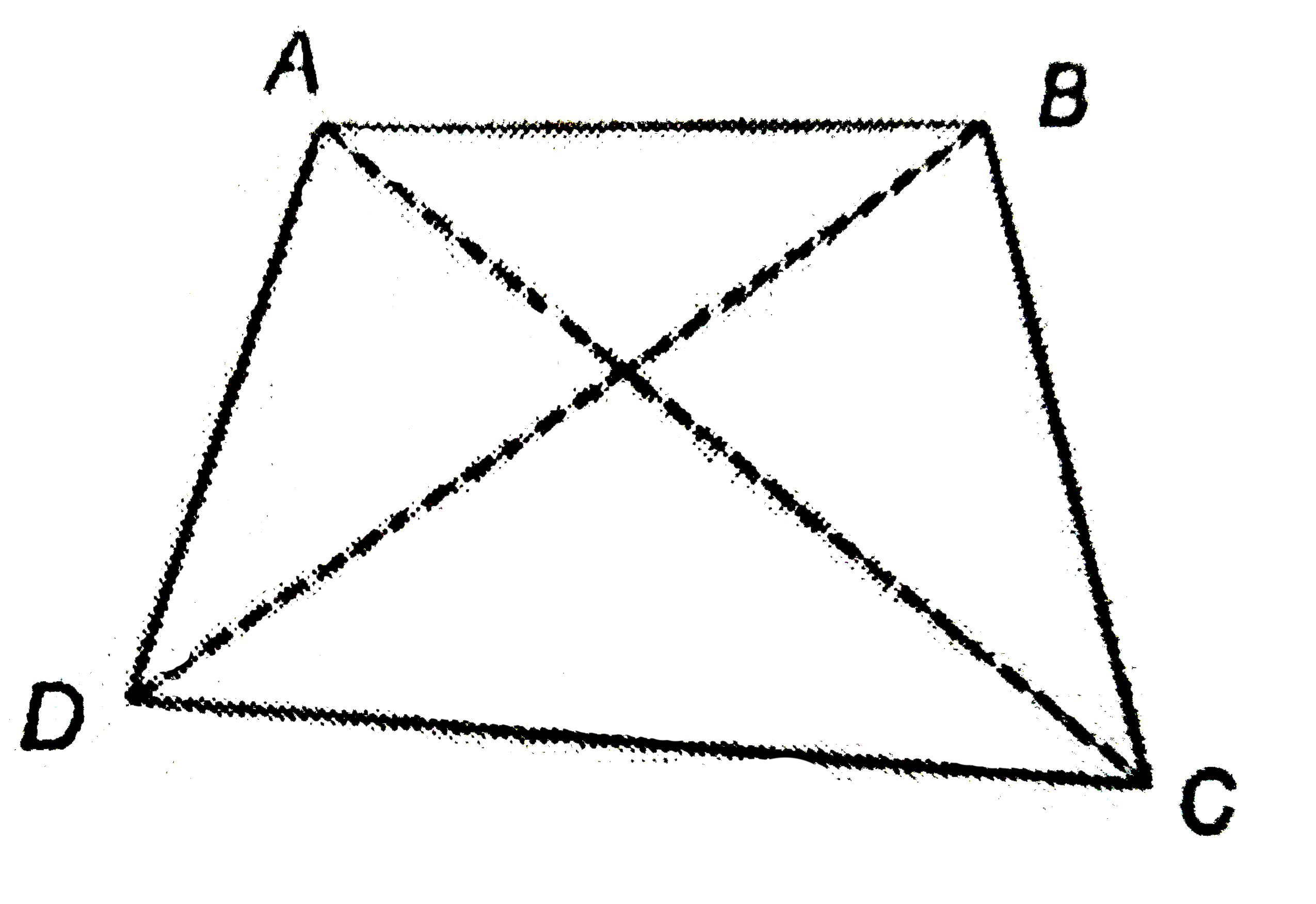
In □ABCD,AB is the smallest and CD is the largest side. Prove that :
(i) ∠B>∠D (ii) ∠A>∠C
Video Solution
Text Solution
(i) join BD.
In ΔABD
A>AB (∵AB is smallest side)
⇒ ∠ABD>∠ADB ...(1)
In ΔBCD
CD>BC (∵CD is largest side)
∠CBD>∠BDC ...(2)
Adding equations (1) and (2)
∠ABD+∠CBD>∠ADB+∠BDC
∠ABC>∠ADC
⇒ ∠B>∠D
(ii) Join AC
In ΔABC
BC>AB (∵AB is smallest side)
∠BAC>∠ACB ...(1)
In ΔACD
CD>AD (∵CD is largest side)
⇒ ∠CAD>∠ACD ...(2)
Adding equations (1) and (2)
∠BAC+∠CAD>∠ACB+∠ACD
⇒ ∠BAD>∠BCD
⇒ ∠A>∠C
|
Topper's Solved these Questions
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Problems From NCERT/exemplar
Explore 5 Videos
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Exercise 7a
Explore 35 Videos
- SURFACE AREA AND VOLUMEBook:NAGEEN PRAKASHANChapter:SURFACE AREA AND VOLUMEExercise:Revision Exercise (long Answer Questions)
Explore 10 Videos
Similar Questions
Knowledge Check
In figure, ∠B<∠Aand∠C<∠D then
 AAD<BCBOD>OCCOB<OADNone of these
AAD<BCBOD>OCCOB<OADNone of theseIn ΔABC,∠A=50∘,∠B=60∘. Find the largest side.
AABBACCBCDall are equal
In △ABC,AC>AB. AB is extended to P and AC is extended to Q. Prove that, ∠PBC<∠QCB.
View SolutionOAOC=ODOB. Prove that ∠A=∠C and ∠B=∠D.
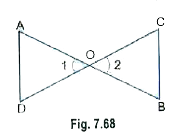
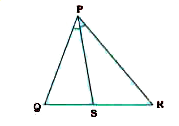
View SolutionIn the given figure, PR > PQ and PS bisects ∠ QPR. Prove that ∠PSR>∠PSQ.
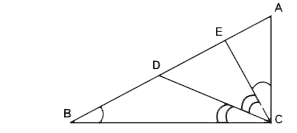
View SolutionIn the figure , CD is the angle bisector of ∠ECB,∠B=∠ACE. Prove that ∠ADC=∠ACD
View SolutionAB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see th e given figure). Show that ∠A>∠C and ∠B>∠D

View SolutionIn a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively. Prove that ∠AOB=12(∠C+∠D).
View Solution


