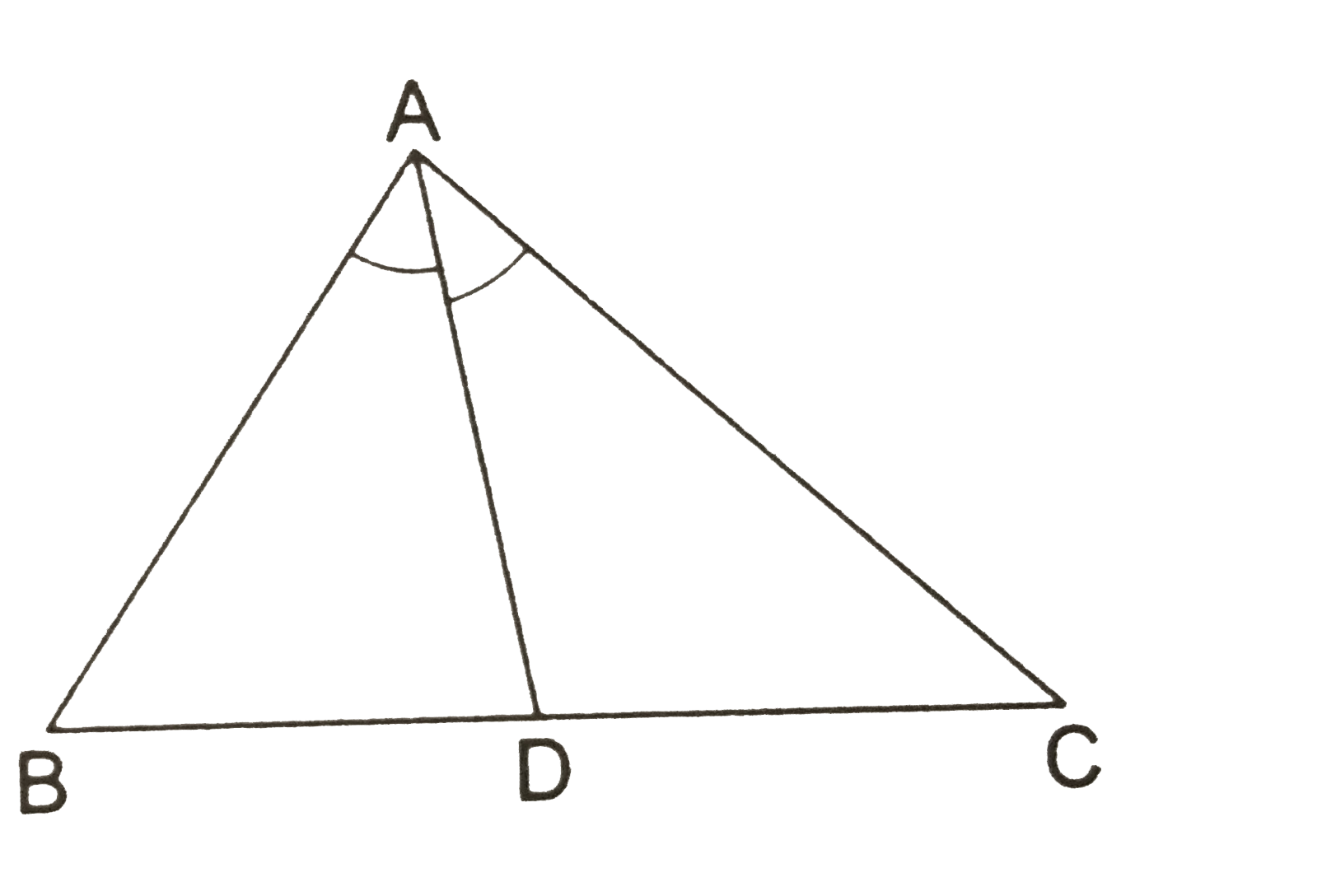
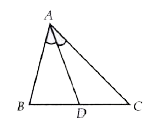
In ΔABC,AD is the bisector of ∠A. Write AB, BD and DC in descending order of their length.

Video Solution
Text Solution
In ΔABC
∠BAC=180∘−∠ABC−∠ACB
=180∘−60∘−40∘=80∘
∴∠BAD=∠CAD=12∠BAC=12×80∘=40∘
In ΔABD
∠ADB=180∘−∠ABD−∠BAD
=180∘−60∘−40∘=80∘
In ΔACD
∠CAD=∠ACD
⇒ CD=AD ...(1)
In ΔABD
∠ADB>∠ABD>∠BAD
⇒ AB>AD>BD
⇒ AB>CD>BD [from (1)]
|
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
Knowledge Check
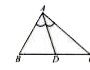
In the adjoining figure, write the sides of ΔABC in descending order of their length.
 ABC, AB, ACBBC, AC, ABCAB, AC, BCDnone of these
ABC, AB, ACBBC, AC, ABCAB, AC, BCDnone of theseIn ΔABC,AD is the bisector of ∠A . Then , ar(ΔABD)ar(ΔACD)=
AAB2AC2BABACCBMCMDNone of theseIn ΔABC,AB=5cm,AC=7cm. If AD is the angle bisector of ∠A Then BD:CD is :
A25:49B49:25C6:1D5:7
In the figure, AD is the bisector of angle BAC. Prove that AB>BD.
View SolutionIn ΔABC,∠B=35∘,∠C=65∘ and the bisector of ∠BAC meets BC in X. Arrange AX, BX and CX in descending order.
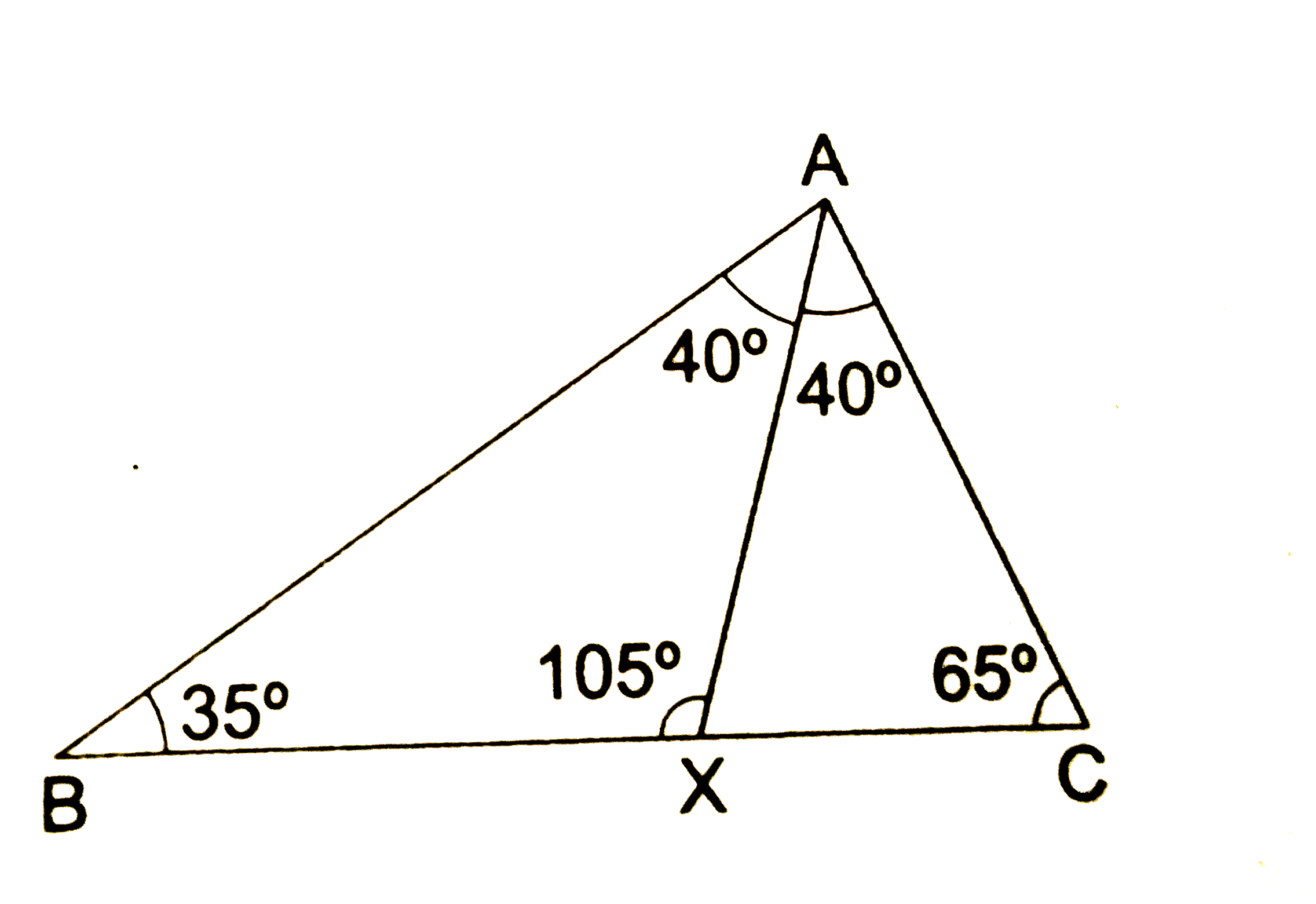
View SolutionRay BD is the angle bisector of ∠ABC. The perimeter of ΔABC is
View SolutionIn a ΔABC,AD is the bisector of ∠A.
(i) If AB=6.4cm,AC=8cmandBD=5.6cm, find DC.
(ii) If AB=10cm,AC=14cmandBC=6cm, find BD and DC.
(iii) If AB=5.6cm,BD=3.2cm,andBC=6cm, find AC.
(iv) If AB=5.6cm,AC=4cm,andDC3cm, find BC.
View SolutionIn ΔABC,AD is the inernal besector of ∠A. If BD = 5cm , BC=7.5 cm , then AB:AC=
View Solution