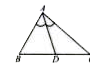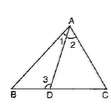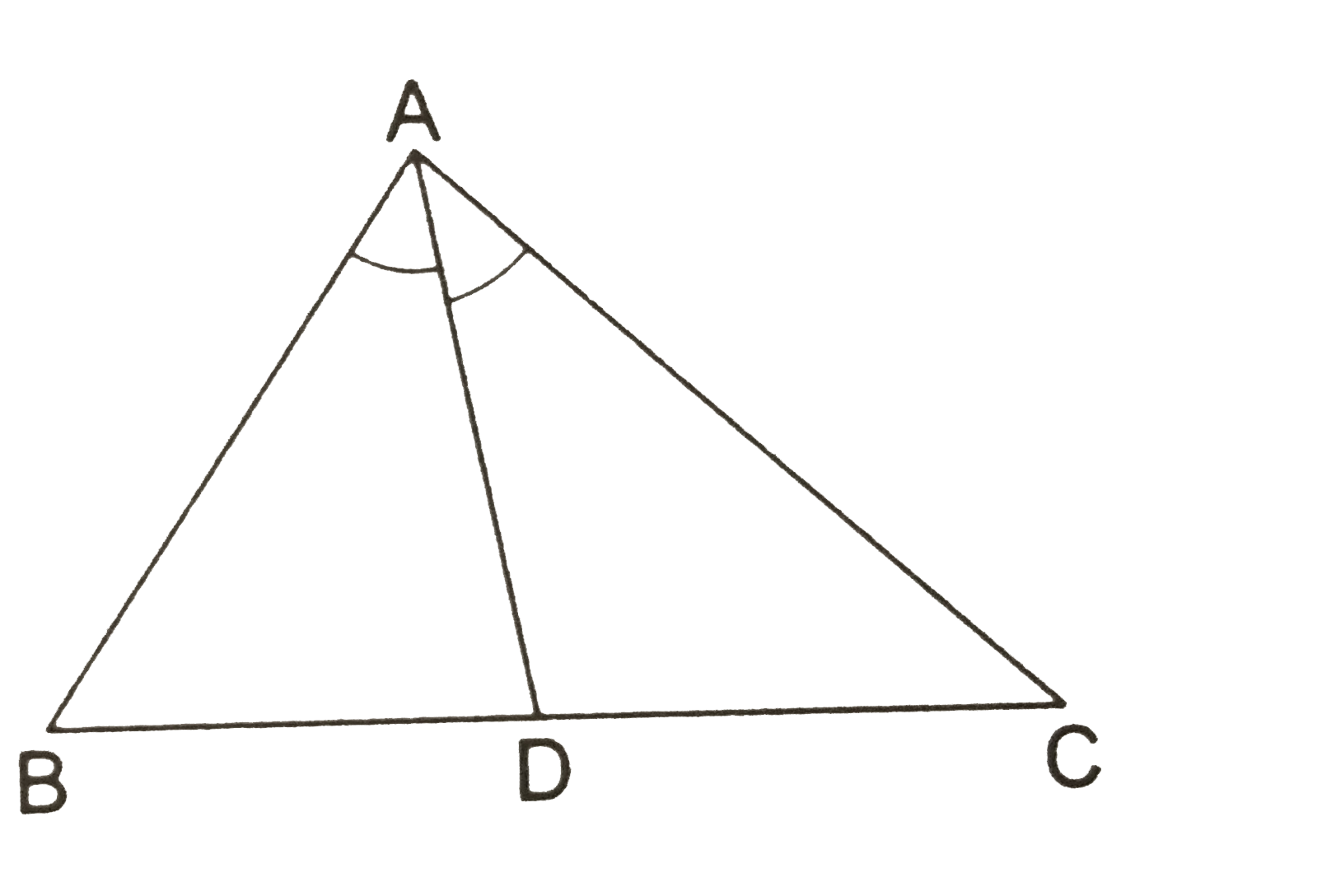
In ΔABC, if AD is the bisector of ∠A, show that AB>BD and AC>DC.
Video Solution
Text Solution
GIVEN A ΔABC in which AD is the bisector of ∠A.
TO PROOF Ab>BDandAC>DC.
PROOF In ΔACD, side CD has been produced to B.
∴ ext. ∠ADB> int. opp. ∠CAD
⇒ ∠ADB>∠CAD
⇒ ∠ADB>∠BAD [∵∠CAD=∠BAD]
⇒ AB>BD [side opposite to large angle is larger].
Again, in ΔABD, the side BD has been produced to C.
∴ ext. ∠ADC> int. opp. ∠BAD
⇒ ∠ADC>∠BAD
⇒ ∠ADC>∠CAD [∵∠BAD=∠CAD]
⇒ AC>DC [side opposite to larger angle is larger].
Hence, AB>BDandAC>DC.
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Exercise 9A
Explore 27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Exercise 9B
Explore 16 Videos
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:MULTIPLE CHOICE QUESTION(MCQ)
Explore 37 Videos
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Multiple Choice Questions (Mcq)
Explore 22 Videos
Similar Questions
Knowledge Check
In ΔABC,AD is the bisector of ∠A . Then , ar(ΔABD)ar(ΔACD)=
AAB2AC2BABACCBMCMDNone of theseIn ΔABC,AB=5cm,AC=7cm. If AD is the angle bisector of ∠A Then BD:CD is :
A25:49B49:25C6:1D5:7
In the given figure, AC>AB and AD is the bisector of ∠A. show that ∠ADC>∠ADB.
View SolutionIn ΔABC,AD is the bisector of ∠A. Write AB, BD and DC in descending order of their length.

View SolutionIn Figure, AC>AB and AD is the bisector of LA . Show that ADC>∠ADB .

View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:

BD = CD
View SolutionIn triangle ABC, AB = 6, AC = 7 and BC = 8. If AD is bisector of angleA , then find the length of BD and CD.
View SolutionIf the lengths of the sides BC, CA and AB of ΔABC are a,b, and c repspectively and AD is the bisector of ∠A then find the length of BD and DC.
View Solution