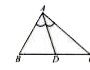
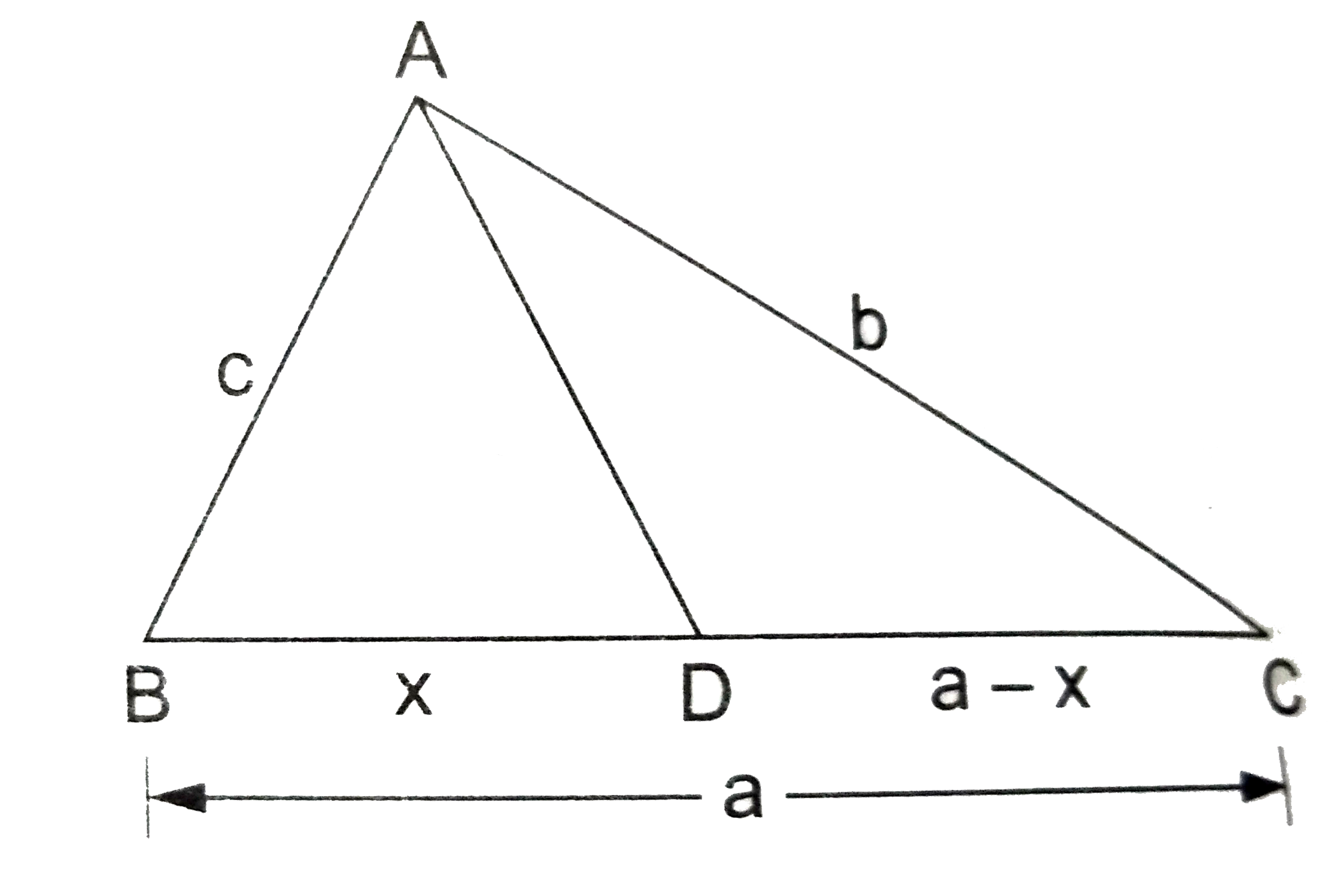
If the lengths of the sides BC, CA and AB of ΔABC are a,b, and c repspectively and AD is the bisector of ∠A then find the length of BD and DC.
Video Solution
Text Solution
The correct Answer is:BD=acb+c'DC=abb+c
Let BD=x , then DC=BC−BD=a−x.
Now, BDDC=ABAC [ by angle-bisector theorem]
⇒xa−x=cb⇒x=acb+candSo,a−x=abb+c
|
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Multiple Choice Questions (Mcq)
Explore 53 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTPILE-CHOICE QUESTIONS (MCQ) ( MATCHING OF COLUMNS)
Explore 1 Video
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7D
Explore 22 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
Knowledge Check
The sides BC, CA and AB of a ΔABC are of lengths a,b and c, respectively. If D is the mid -point of BC and AD is perpendicular to AC, then the value of cos A cos C is
A3(a2−c2)2acB(2a2−c23bcCa2−c23acD2(c2−a2)3acThe lengths of the sides of a trlangle are a,bandc respectively. If a2+b2+c2=ab+bc+ca, then the triangle is:
AisoscelesBequilateralCscaleneDright-angledThe in circle of ΔABC touches the sides BC, CA and AB at D, E and F respectively. Then AF + BD + CE is equal to :
A12 (Perimeter of Δ ABC)B13 (Perimeter of Δ ABC)C14 (Perimeter of Δ ABC)DPerimeter of Δ ABC
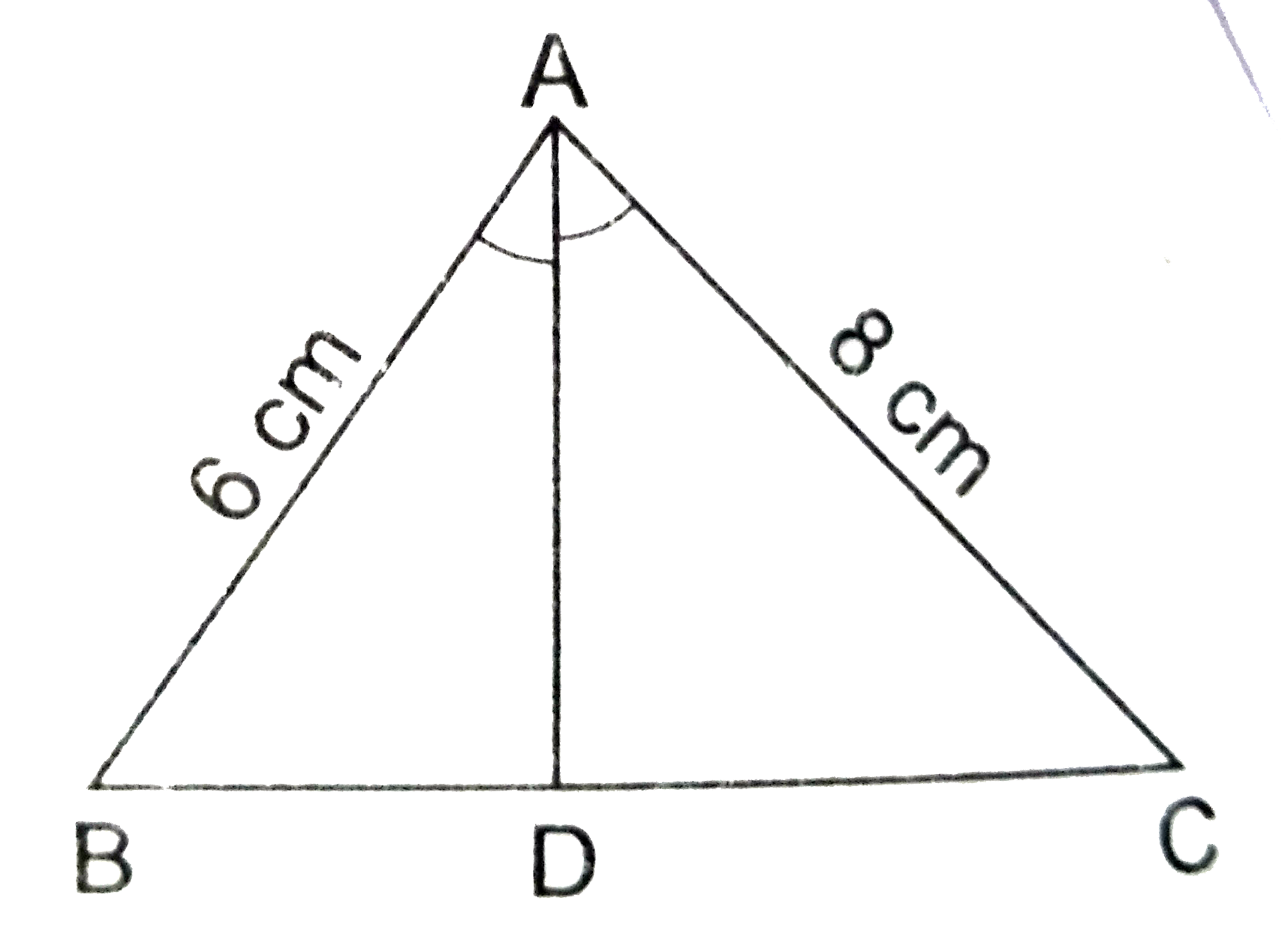
In aΔABC it is given that AB=6cm,AC=8cmandAD is the bisector of ∠A. Then BD:DC=?
View SolutionIn ΔABC,AD is the bisector of ∠A. Write AB, BD and DC in descending order of their length.

View SolutionIn a ΔABC, AC = 12 cm, AB = 16 cm and AD is the bisector of ∠A. If BD = 4 cm, then what is DC equal to ?
View SolutionIn a triangle ABC, ∠B=90∘,AB=8cm,BC=6cm. BD is perpendicular to AC, then find the length of CD, AD and BD.
View SolutionIn ΔABC,AB=12cm,BC=16cm and CA=20cm If D is the mid point of AC then the length of BD is
View Solution