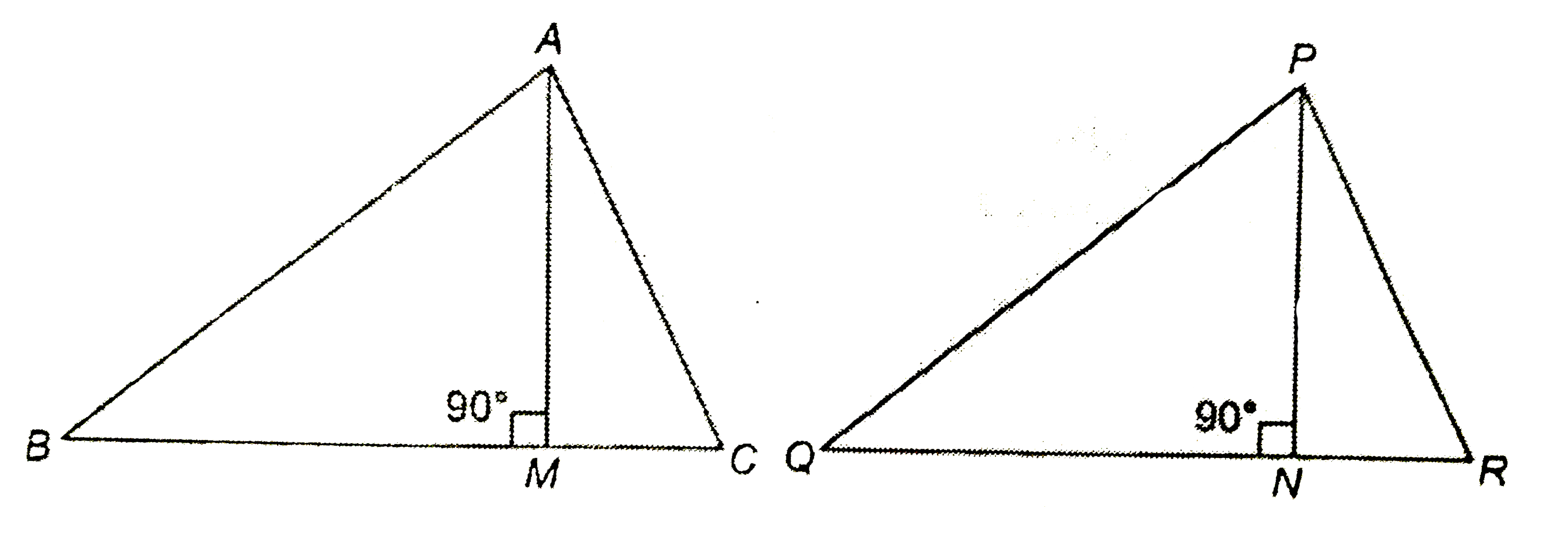
In the given figure, the two sides AB and BC, and the median AD of ΔABC are correspondingly equal to the two sides PQ and QR, and the medium PM of ΔPQR. Prove that ΔABC≅ΔPQR.
GIVEN ΔABCandΔPQR in which AB = PQ, BC = QR and median AD of ΔABC=median PM of ΔPQR.
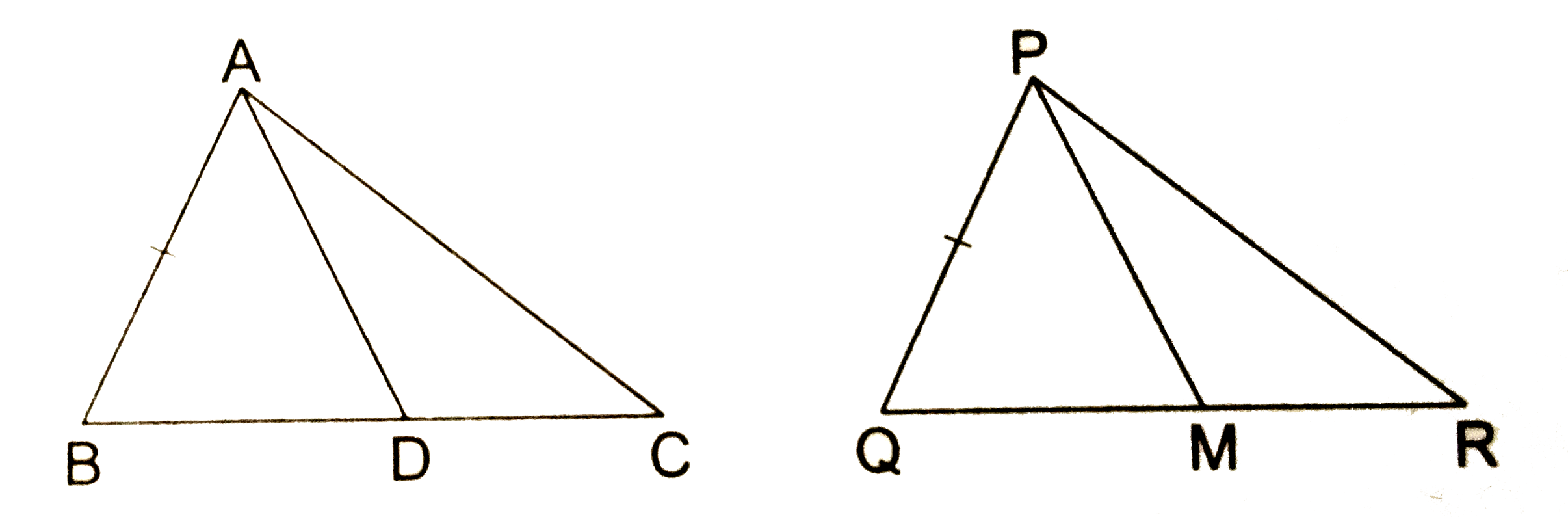
TO ROVE ΔABC≅ΔPQR.
PROOF In ΔABDandΔPQM, we have
AB=PQ (given)
BD=QM [∵BC=QR⇒12BC=12QR⇒BD=QM]
med. AD = med. PM (given)
∴ ΔABD≅ΔPQR (SSS-criteria).
∴ ∠ABD=∠PQM (c.p.c.t.).
⇒ ∠ABC=∠PQR.
Now, in ΔABCandΔPQR, we have
AB=PQ (given)
∠ABC=∠PQR (proved above)
BC=QR (given).
∴ ΔABC≅ΔPQR (SAS-criteria).
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
The sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see figure). Show that

ΔABM≅ΔPQN
View Solution
Knowledge Check
In the given figure, the two sides AB and BC, and the median AD of ΔABC are correspondingly equal to the two sides PQ and QR, and the medium PM of ΔPQR. Prove that ΔABC≅ΔPQR.
AΔABD≅ΔPQMBΔABC≅ΔPQRCΔABD≅ΔPMRDΔADC≅ΔPMR
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC~ΔPQR.
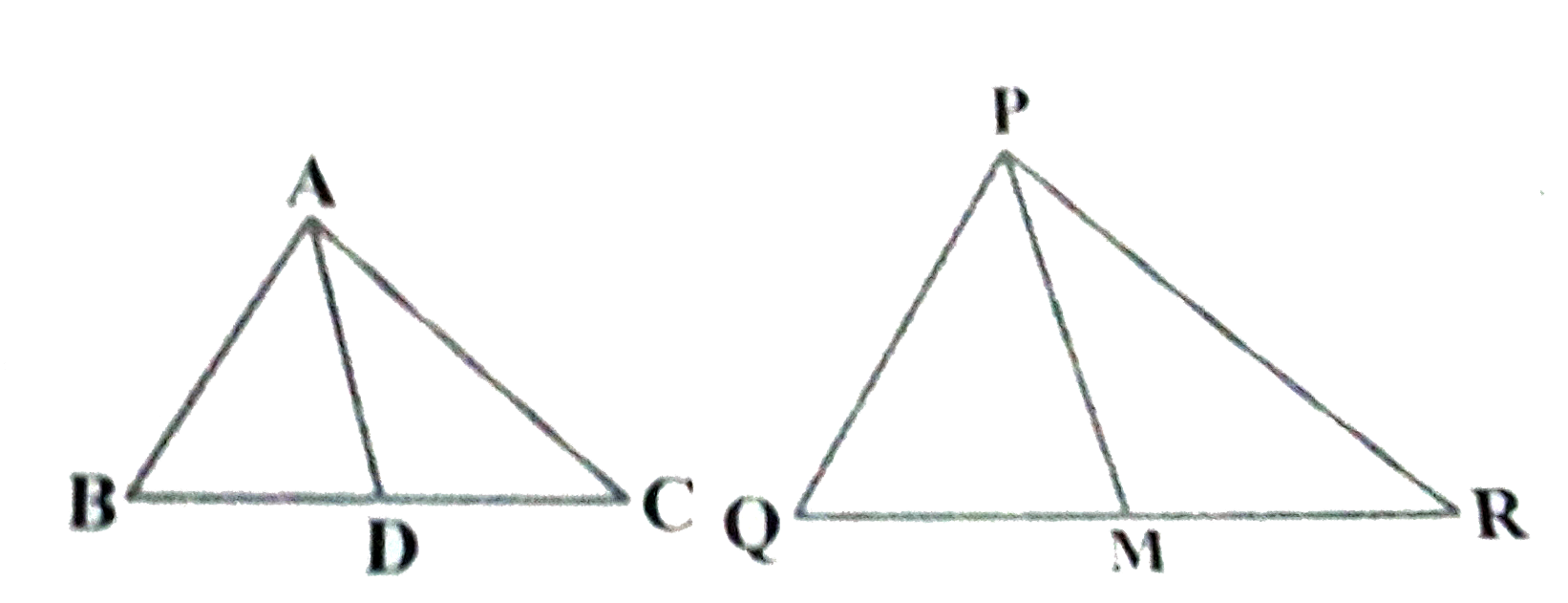
View SolutionSides AB and BC and median AD of a triangle ABC are respectively propor-/ tional to sides PQ and QR and median PM of ΔPQR (see Fig. 6.41). Show that ΔABC~ΔPOR.
View SolutionSides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Prove that ΔABC~DetlaPQR
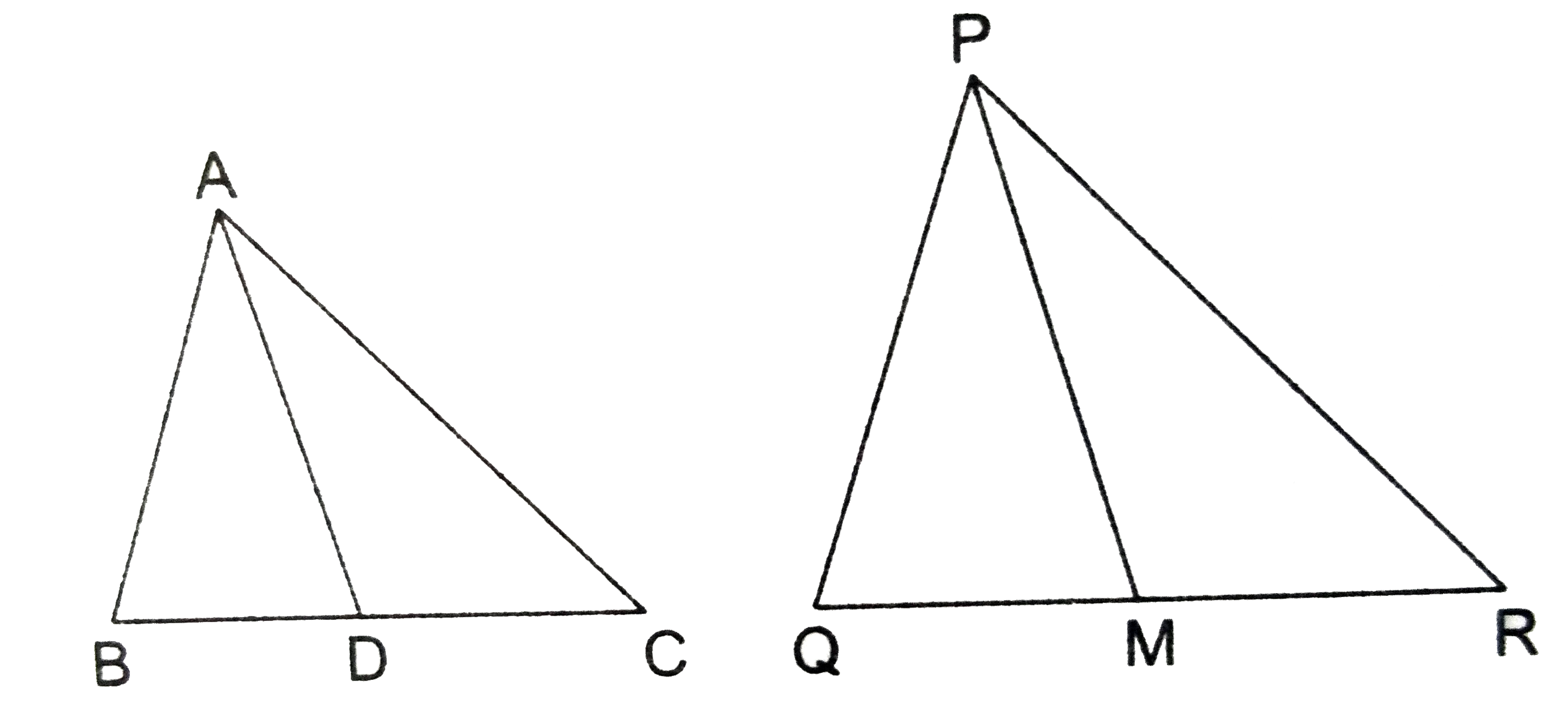
View SolutionThe sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
View SolutionIn the given figure, PQ||ABandPR||AC.
Prove that QR∣∣BC
View SolutionIn ΔABC,L,M,Nare points on side AB,BC,AC respectively.
Perpendiculars drawn at L,M,N form ΔPQR.
Prove that ΔABC~ΔPRQ.
View SolutionIn the following figures, AB=PQ,AC=PR and AM=PN. Prove that ΔABC≅ΔPQR.
View Solution
