Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Prove that $Δ A B C ~ D e t l a P Q R$

Video Solution

Text Solution

Verified by Experts

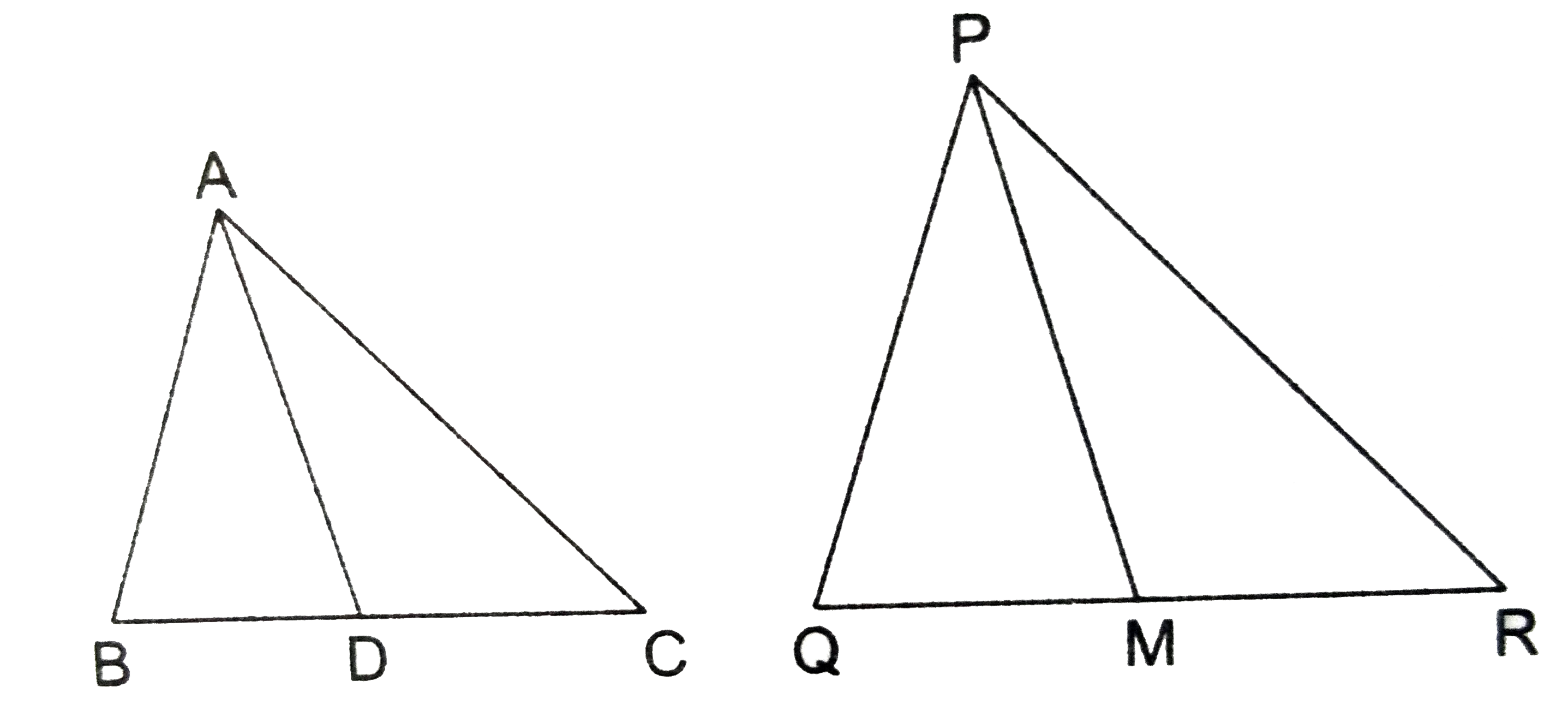
GIVEN AD and PM ar medians of $Δ A B C and Δ P Q R$ respectively such that
$\frac{A B}{P Q} = \frac{A C}{P R} = \frac{A D}{P M}$
TO PROVE $Δ A B ~ Δ P Q R$
CONSTRUCTION Produce AD to E such that AD= DE and produce PM to N such that PM= MN.
Join EC and NR.

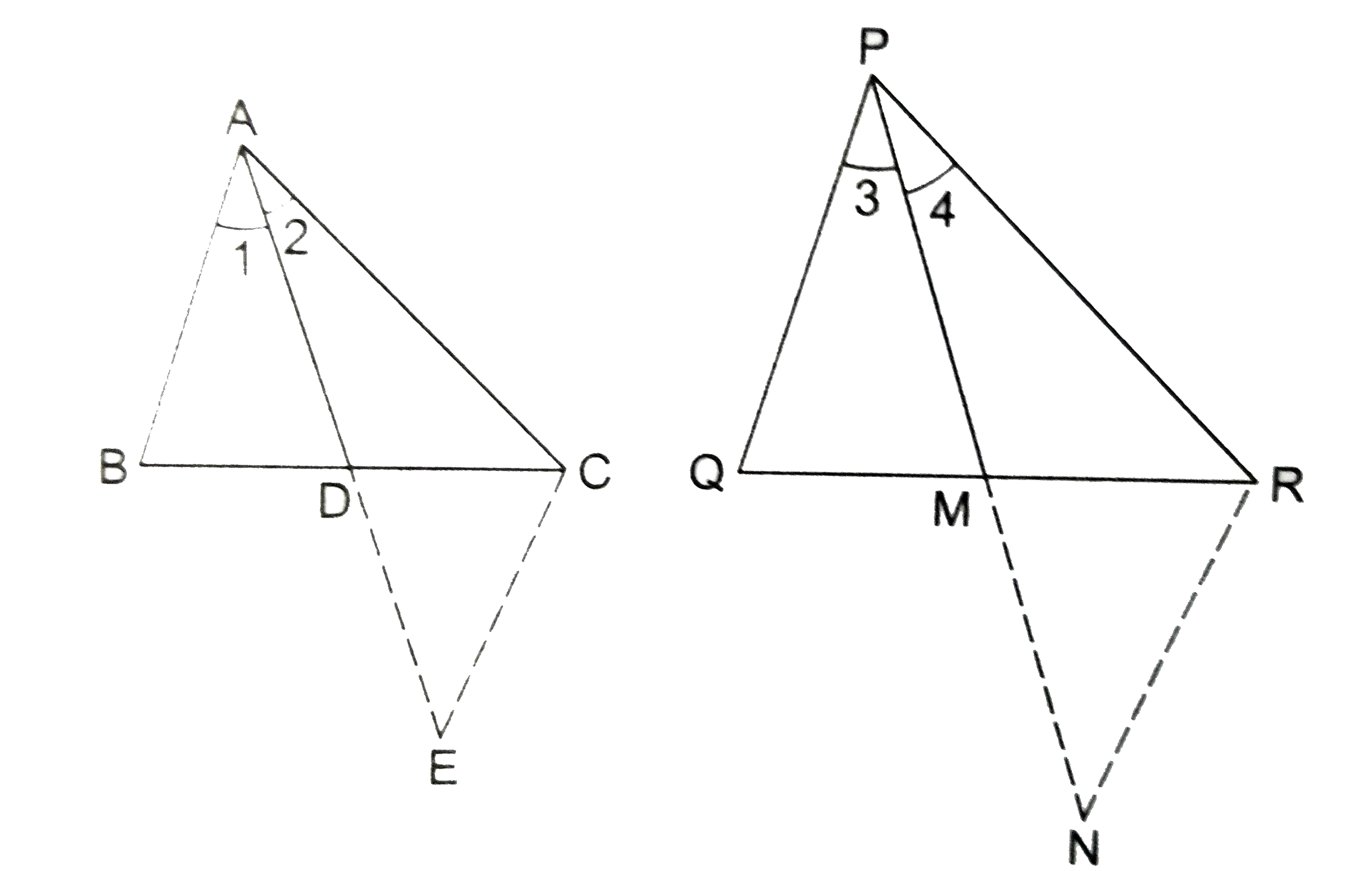
PROOF In $Δ A B D and Δ E C D$ , we have
$B D = C D [∴ D$ is midpoint of BC]
AD= ED [ by construction]
$∠ B D A = ∠ C D E$ [ vertices opposite angels]
$∴ Δ A B D ≅ Δ E C D$ [ by SAS- contruency]
And so, $A B = E C ... . (i)$ [cpct]
Similarly, $Δ P Q M ≅ Δ N R M$
and So, $P Q = N R ... . (i i)$ [ cpct]
Now, $\frac{A B}{P Q} = \frac{A C}{P R} = \frac{A D}{P M}$ (given)
$\Rightarrow \frac{E C}{N R} = \frac{A C}{P R} = \frac{A D}{P M}$ [ using (i) and (ii)]
$\Rightarrow \frac{E C}{N R} = \frac{A C}{P R} = \frac{2 A D}{2 P M} = \frac{A E}{P N} [∴ 2 A D = A E, 2 P M = P N]$
$\Rightarrow Δ A C E ~ Δ P N R$ [ SSS- similarity]
$∴ ∠ 2 = ∠ 4$ [ corresponding angels of similar triangles are equal]
Similarly, $∠ 1 = ∠ 3$ = [ it can be proved by joining BE and QN and showing $Δ A B E ~ Δ P Q N$ ]
$∴ ∠ 1 + ∠ 2 = ∠ 3 + ∠ 4, i . e ., ∠ B A C = ∠ Q P R . ... . (i i i)$
Now, in $Δ A B C and Δ P Q R$ , we have
$\frac{A B}{P Q} = \frac{A C}{P R}$ [ given]
$∠ B A C E = ∠ Q P R$ [ form (ii)]
$∴ Δ A B C D ~ Δ P Q R$ [ by SAS-similarity]

Updated on:21/07/2023

If PS is median of the triangle PQR, then ar( $Δ$ PQS): ar( $Δ$ QRP) is

A1 : 1
B2 : 1
C1 : 2
DCan't be determined
Points P and Q lie on sides AB and AC of triangle ABC respectively such that segment PQ is parallel to side BC. If the ratio of areas of triangle APQ: triangle ABC is 25 : 36, then the ratio PA : PB is
A $5 : 6$
B $1 : 5$
C $6 : 5$
D $5 : 1$