Two lines L1x=5,y3−α=z−2andL2:x=αy−1=z2−α are coplanar. Then α can take value (s) a. 1 b. 2 c. 3 d. 4

A

1

B

2

C

3

D

4

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A, D

If two straight lines are coplanar,
i.e. x−x1a1=y−y1b1=z−z1c1
and x−x2a2=y−y2b2=z−z2c2 are coplanar
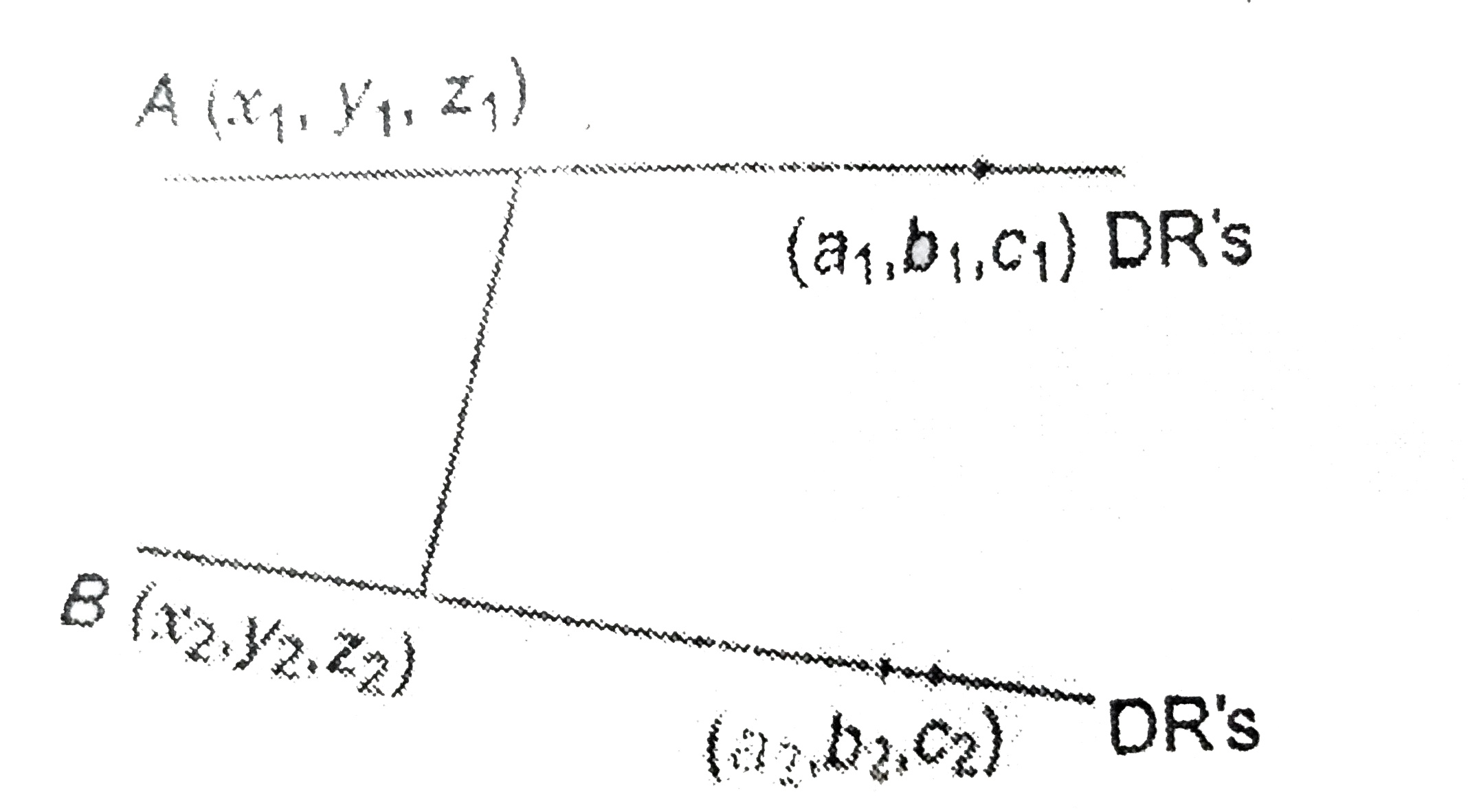
ocr_image
Then, (x2−x1,y2−y1,z2−z1),(a1,b1,c1) and (a2,b2,c2) are coplanar.
i.e. ∣∣ ∣ ∣∣x2−x1y2−y1z2−z1a1b1c1a2b2c2∣∣ ∣ ∣∣=0
Here, x=5,y3−α=z−2
⇒ x−50=y−0−(α−3)=z−0−2 ...(i)
and x−α,y−1=z2−α
⇒ x−α0=y−0−1=z−02−α ...(ii)
⇒ ∣∣ ∣∣5−α 0 0 03−α −2 0−12−α∣∣ ∣∣=0
⇒ (5−α)[(3−α)(2−α)−2]=0
⇒ (5−α)[a2−5α+4]=0
⇒ (5−α)(α−1)(α−4)=0
∴ α=1,4,5

Updated on:21/07/2023
|
Class 12MATHSTHREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Two lines L1:x=5,y3−α=z−2
    L2:x=α,y−1=z2−α are coplanar. Then, α can take value (s)

    A1, 4, 5
    B1, 2, 5
    C3, 4, 5
    D2, 4, 5

  • Two lines L1:x=5,y3−α=z−2andL2:x=α,y−1=z2−α are coplanar. Then, α can take value(s)

    A1
    B2
    C3
    D4

  • Two lines L1:x=5,y3−α=z−2andL2:x=α,y−1=z2−α are coplanar. Then, α can take value(s)

    A1
    B2
    C3
    D4