The distance from the point −ˆi+2ˆj+6ˆk to the straight line through the point (2,3,-4) and parallel to the vector 6ˆi+3ˆj−4ˆk, is
2√3
4√3
6
7
The correct Answer is:D
Let point P whose position vector is (−ˆi+2ˆj+6ˆk) and a stright line passing through Q(2, 3, -4) parallel to the vector n=6ˆi+3ˆj−4ˆk.
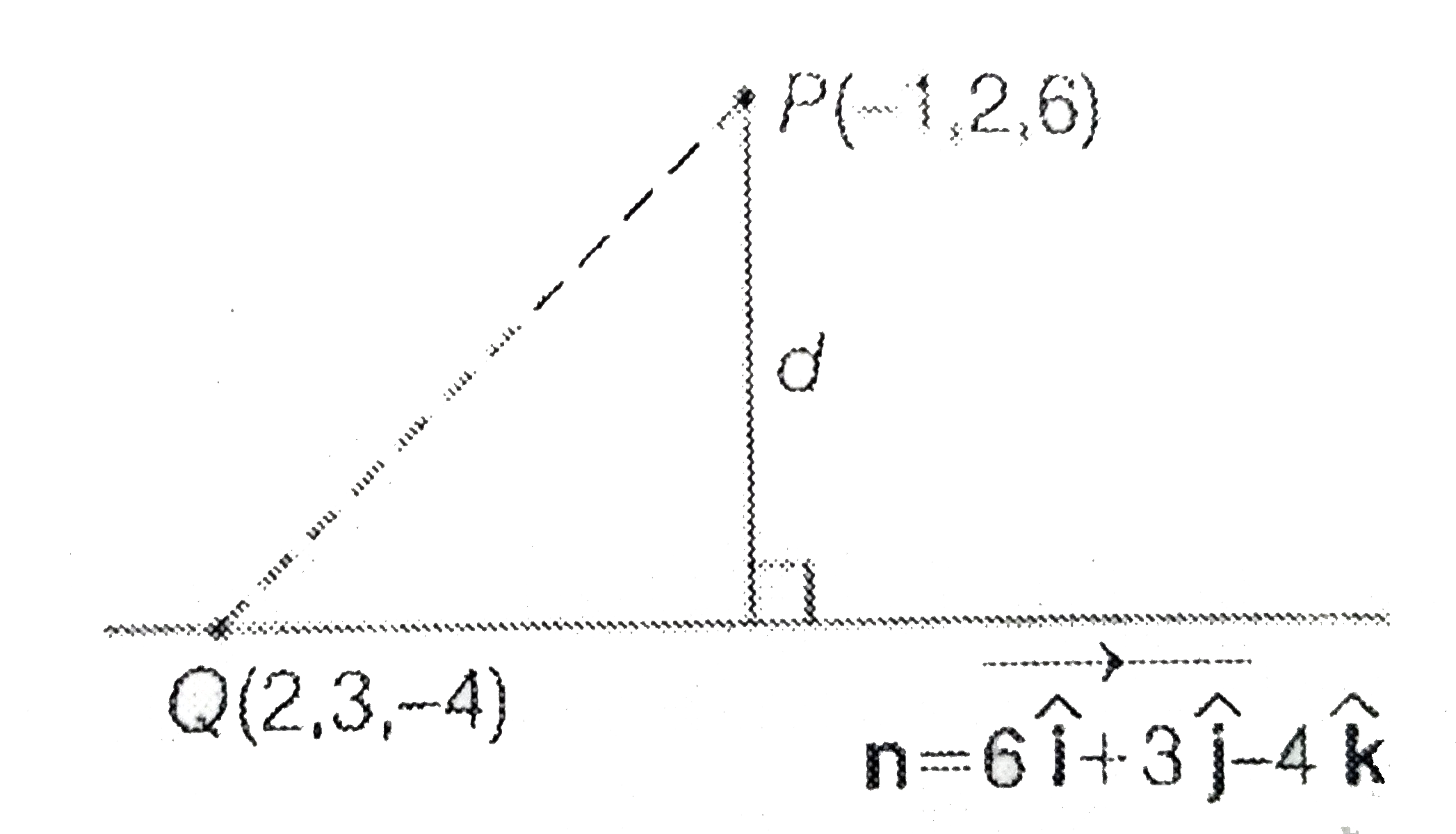
∵ Required distance d=Projection of line segment PQ perpendicular to vector n.
=|PQ×n||n|
Now, PQ=3ˆi+ˆj−10ˆk, so
PQ×n=∣∣
∣
∣∣ˆi ˆj ˆk3 1−106 3−4∣∣
∣
∣∣=26ˆi−48ˆj+3ˆk
So, d=√(26)2+(48)2+(3)2√(6)2+(3)2+(4)2
=√676+2304+936+9+16=√298961
=√49=7units
Topper's Solved these Questions
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Straight Line in Space and Shortest Distance Objective Question II (One or more than one correct option)
3 Videos
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question I (Only one correct option)
49 Videos
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (Integer Answer Type Question)
1 Videos
- PROPERTIES OF TRIANGLESBOOK - IIT JEE PREVIOUS YEARCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - CIRCUMCIRCLE, INCIRCLE, ESCRIBED CIRCLE, ORTHOCENTRE,INCENTRE AND CIRCUMCENTRE
20 Videos
- APPLICATION OF DERIVATIVES BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA ( INTEGER ANSWER TYPE QUESTIONS)
8 Videos
Similar Questions
Knowledge Check
The distance of the point having position vector −ˆi+2ˆj+6ˆk from the straight line passing through the point (2,3,−4) and parallel to the vector, 6ˆi+3ˆj−4ˆk is :
A2√13B4√3C6D7The equation of a line passing through the point (4,-2,5) and parallel to the vector 3ˆi−ˆj+2ˆk is
Ax−43=y+2−1=z−52Bx+43=y−2−1=z+52Cx−34=y+1−2=z−25Dx+34=y−1−2=z+25The distance of the point P(1,2,3) from the line which passes through the point (4,2,2) and parallel to the vector 2ˆi+3ˆj+6ˆk is
A√10B√7C√5D1
Find the vector and cartesian equation of the line passing through the point P (1,2,3) and parallel to the planes :
→r.(ˆi−ˆj+2ˆk)=5. →r.(3ˆi+ˆj+ˆk)=6.
View SolutionThe position vector of a point at a distance of 3√11 units from ˆi−ˆj+2ˆk on a line passing through the points ˆi−ˆj+2ˆk and parallel to the vector 3ˆi+ˆj+ˆk is
View SolutionLet →OB=ˆi+2ˆj+2ˆk and→OA=4ˆi+2ˆj+2ˆk . The distance of the point B from the straight line passing through A and parallel to the vector 2ˆi+3ˆj+6ˆk is
View SolutionThe equation of plane passing through point (3 ,4 ,5) and parallel to the vectors ˆi+2ˆj+3ˆkand3ˆi+2ˆj+4ˆk is
View SolutionThe vector equation of the plane passing through the point (-1, 2,-5) and parallel to the vectors 4ˆi−ˆj+3ˆk and ˆi+ˆj−ˆk is
View Solution
