Given : 15cotA=8 find sinAandsecA
Video Solution
Text Solution
The correct Answer is:sinA=1517,secA=178
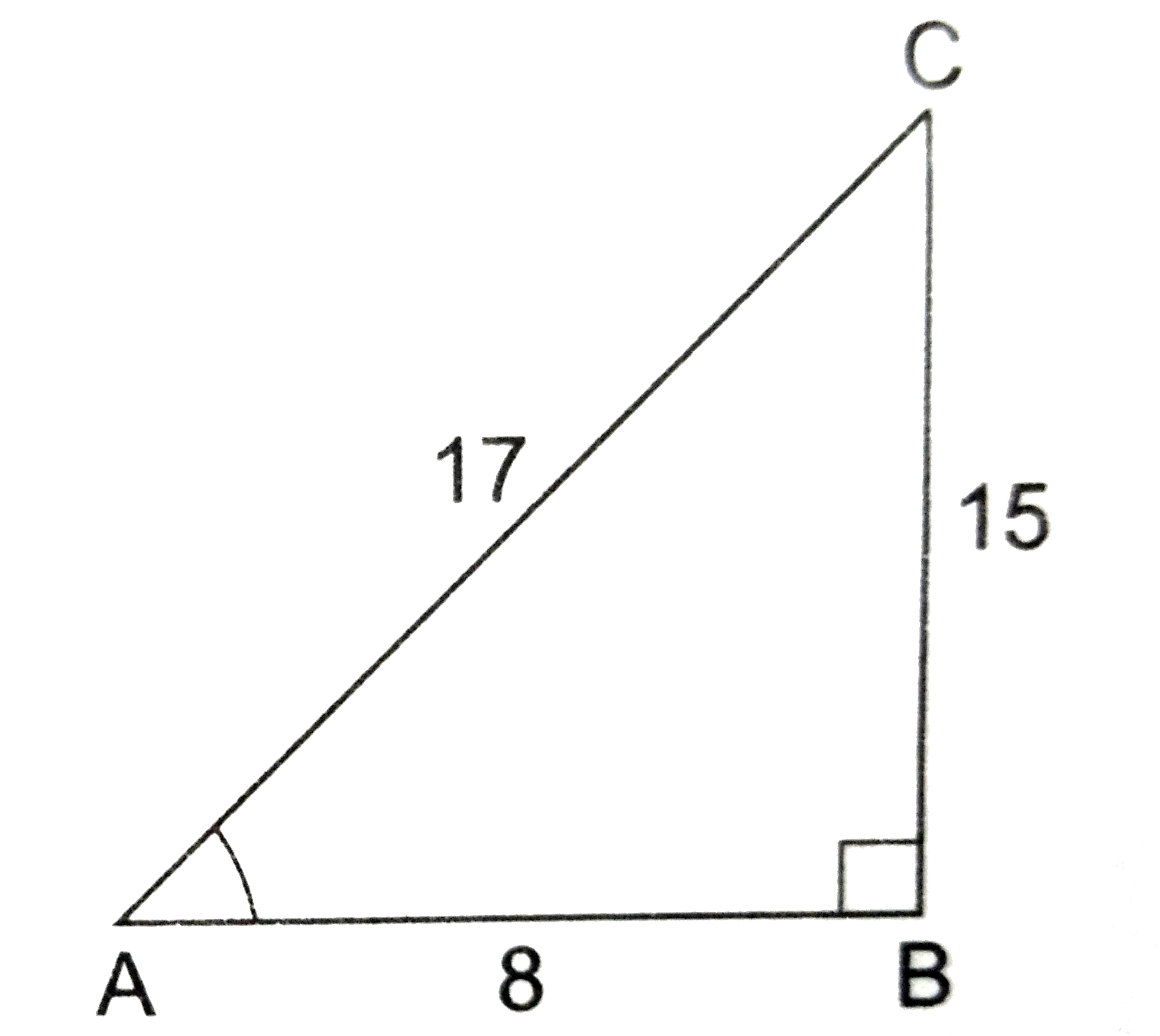
cotA=815⇒tanA=158=BCAB.
∴AC2=AB2+BC2=(8)2+(15)2=64+225=289
⇒AC=√289=17.
∴sinA=BCAC=1517andsecA=ACAB=(17)=(8).
|
Topper's Solved these Questions
- TRIGONOMETRIC RATIOSBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOSEXERCISE - Exercise 10
35 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
- TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES EXERCISE - Exercise 12
15 Videos
Similar Questions
Knowledge Check
If 15 cotA=8, the value of sinA is :
A817B1517C178D1715If 0<A<π/2 and sinA + cosA + tan A + cotA + secA + cosec A=7 and sinA and cosA are roots of equation 4x2−3x+a=0. Then value of 25a is:
A28B30C26D32
Given 15cotA=8, find sinA and secA.
View SolutionIf 15cotA=8, then find the value of cosecA.
View SolutionIf 3sinA+4cosA=4, then find 4sinA−3cosA.
View SolutionGiven tanA=43 then find cosecAcosA−secA
View SolutionIf cosecA−cotA=1.3, then find the value of cosecA+cotA .
View Solution3n Let- is << Tt then 2 cota +sinº asina - cos asina + cos asinasin a- sina + cosasin a(4)-sina – cos asinaT. 5TH. 7TT ...
View Solution
