If 3cotθ=4 then show that 1−tan2θ1+tan2θ=(cos2θ−sin2θ)
Video Solution
Text Solution
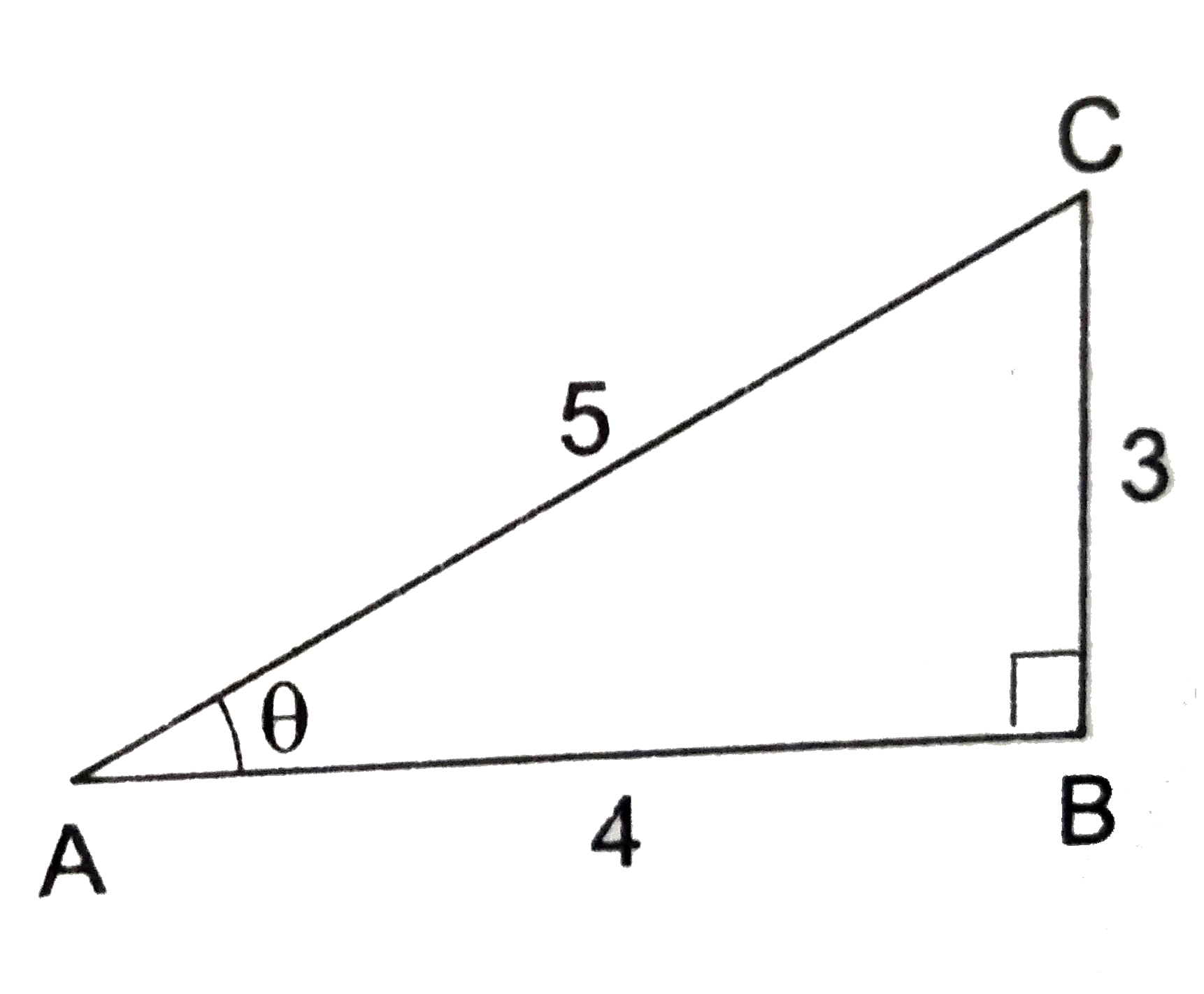
cotθ=43=ABBC.
∴AC2=AB2+BC2=(4)2+(3)2=16+9=25⇒AC=5.
∴sinθ=35,cosθ=45andtanθ=34.
|
Topper's Solved these Questions
- TRIGONOMETRIC RATIOSBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOSEXERCISE - Exercise 10
35 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
- TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES EXERCISE - Exercise 12
15 Videos
Similar Questions
If 3cotθ=4 then show that 1−tan2θ1+tan2θ=(cos2θ−sin2θ)
View SolutionShow that, 1+tan2θ1+cot2θ=tan2θ
View SolutionProve that : 1−tan2θ1+tan2θ=cos2θ−sin2θ
View SolutionProve that : tan2θ1+tan2θ+cot2θ1+cot2θ=1
View SolutionShow that :3(tan2θ+cot2θ)−9(cotθ+tanθ)+10>0
View Solutionprove that sec2θ−sin2θtan2θ=1+cot2θ−cos2θ
View SolutionProve that 1+tanθ1−tanθ=1−sin2θcos2θ.
View Solutioncosθ(tanθ+2)(2tanθ+1)=2secθ+5sinθ
View Solutioncosθ(tanθ+2)(2tanθ+1)=2secθ+5sinθ
View Solutioncosθ(tanθ+2)(2tanθ+1)=2secθ+5sinθ
View Solution
