If sinθ=a2=b2a2+b2 , find the values of other five trigonometric ratios.
Video Solution
Text Solution
The correct Answer is:sinθ=a2−b2a2+b2,cosθ=2aba2+b2,tanθ=a2−b22ab,
cosec θ=a2+b2a2−b2,secθ=a2+b22ab,cotθ=−2aba2−b2
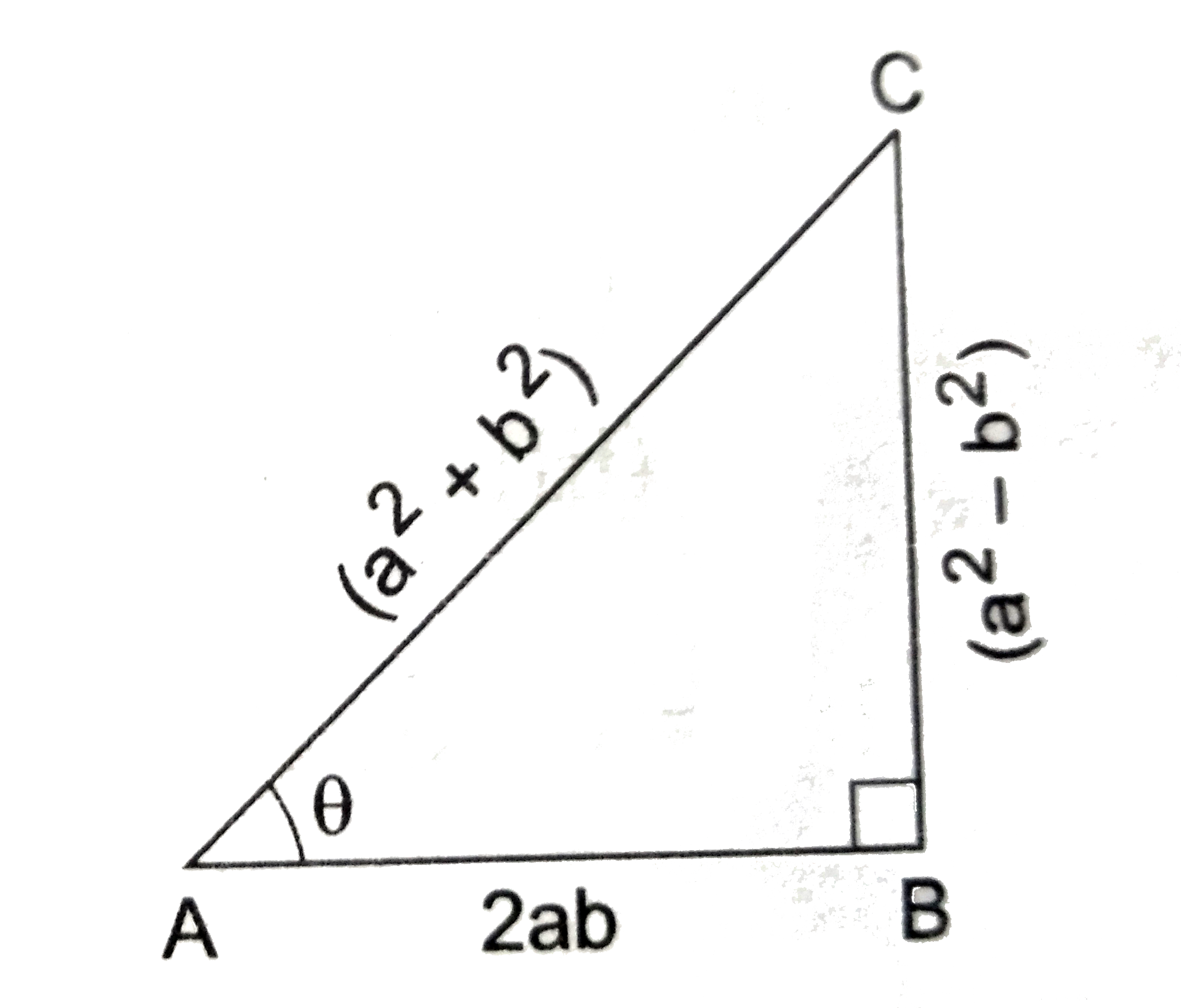
In right ΔABC,∠B=90∘and∠BAC=θ.
Given : sinθ=a2−b2a2+b2=BCAC.
Let BC=(a2−b2)andAC=(a2+b2). Then
AB2=(AC2−BC2)=(a2+b2)2−(a2−b2)2=4a2b2
⇒AB=2ab.
Now , we can find all the T-ratios of θ.
|
Topper's Solved these Questions
- TRIGONOMETRIC RATIOSBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOSEXERCISE - Exercise 10
35 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
- TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES EXERCISE - Exercise 12
15 Videos
Similar Questions
Knowledge Check
Find the values of the following trigonometric ratios :
Acos225∘Bsin690∘Ctan(−390∘)Dsec855∘
If secθ=1312, find the values of other trigonometric ratios.
View SolutionIf sinθ=35 , find the values of other trigonometric ratios.
View SolutionIf tanθ=2021 , then find the values of other trigonometric ratios .
View SolutionIf cosB=13, find the other five trigonometric ratios.
View SolutionIf tanθ=11 , find other trigonometric ratios
View SolutionIf cosecA=√10, find other five trigonometric ratios.
View SolutionIf cosθ=817 , find the other five trigonometric ratios.
View Solution
