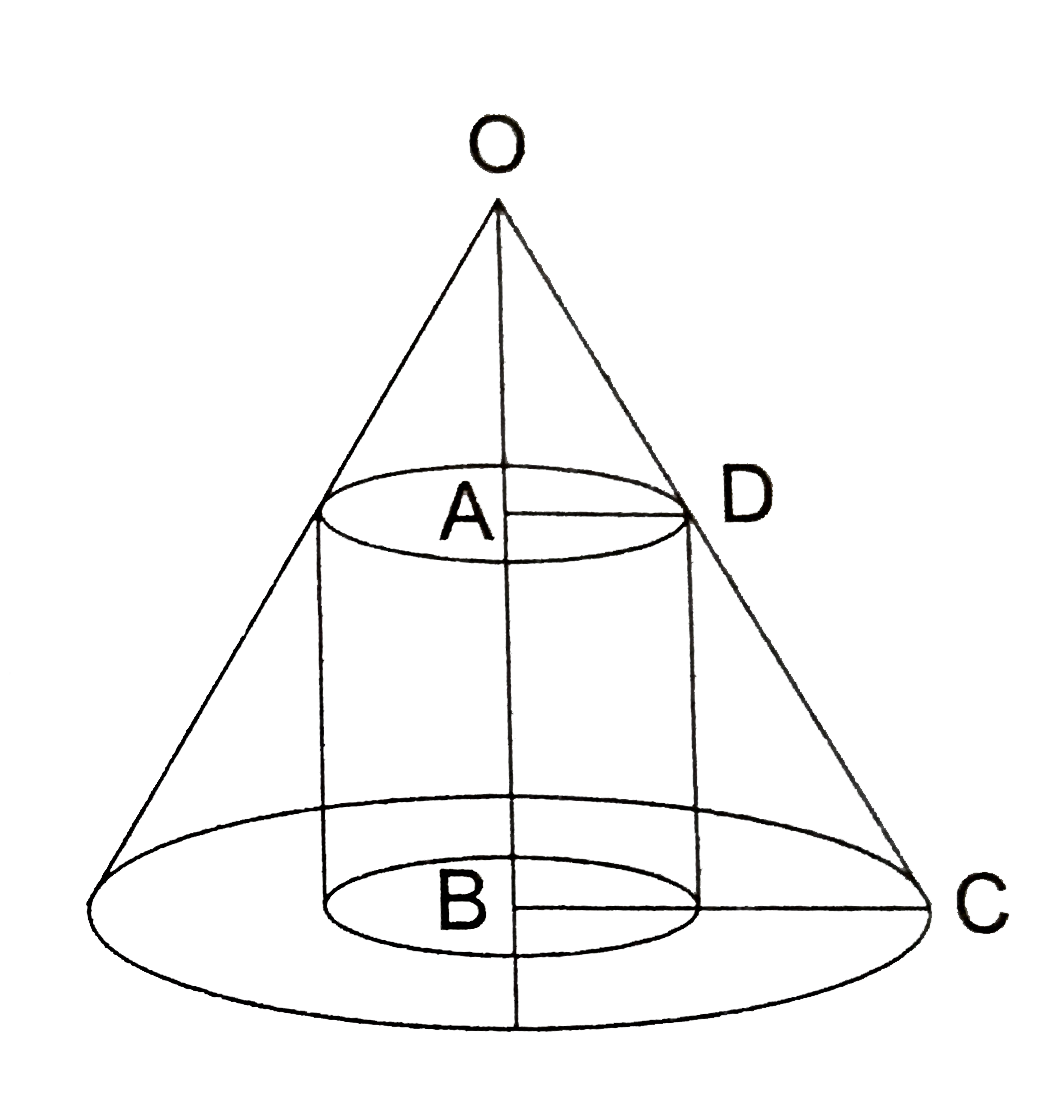
A right circular cylinder is inscribed in a cone. Show that the curved surface area of the cylinder is maximum when the diameter of the cylinder is equal to the radius of the base of the cone.
Let be the radius of the cone and be its height and let r be the radius and h the height of the inscribed cylinder.
Clearly, are similar.
...(i)
Let S be the curved surface area of the cylinder
Then,
Now, . Also,
So, S is maximum when
= diameter of the cylinder
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBook:RS AGGARWALChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 11G
Explore 32 Videos
- APPLICATIONS OF DERIVATIVESBook:RS AGGARWALChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 11H
Explore 30 Videos
- APPLICATIONS OF DERIVATIVESBook:RS AGGARWALChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 11E
Explore 22 Videos
- ADJOINT AND INVERSE OF A MATRIXBook:RS AGGARWALChapter:ADJOINT AND INVERSE OF A MATRIXExercise:Exercise 7
Explore 37 Videos
- AREA OF BOUNDED REGIONS Book:RS AGGARWALChapter:AREA OF BOUNDED REGIONS Exercise:Exercise 17
Explore 39 Videos
Similar Questions
Knowledge Check
A solid metallic right cone is melted and some solid right circular cylinders are made. If the radius of base of each cylinder is half the radius of cone and the height of each cylinder is one third the height of the cone, then the number of cylinders formed are.
A3B4C5D6
Prove that the cylinder inscribed in a right circular cone has maximum curved surface area if the radius of cylinder is half the radius of cone.
View SolutionA cube is inscribed in a sphere. A right circular cylinder is within the cube touching all the vertical faces. A right circular cone is insido tho cylinder. Their heights are same and the diameter of the cone is equal to that of the cylinder.
What is the ratio of the volume of the sphere to that of the cone ?
View SolutionA cube is inscribed in a sphere. A right circular cylinder is within the cube touching all the vertical faces. A right circular cone is insido tho cylinder. Their heights are same and the diameter of the cone is equal to that of the cylinder.
What is the ratio of the volume of the cube to that of the cylinder ?
View SolutionA right circular cylinder circumscribes a sphere of radius r. Find the ratio of the surface area of the sphere to the curved surface area of the cylinder.
View SolutionCurved surface area of a right circular cylinder is 4.4m2. If the radius of the base of the cylinder is 0.7 m, find its height.
View SolutionCurved surface area of a right circular cylinder is 4.4 m2. If the radius of the base of the cylinder is 0.7m, find its height.
View SolutionA solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom Find the volume of water left in the cylinder if the radius of the cylinder is equal to the radius to the cone.
View Solution