Prove that the cylinder inscribed in a right circular cone has maximum curved surface area if the radius of cylinder is half the radius of cone.

Video Solution

Text Solution

Verified by Experts

Let the height of cone = $h$ and semivertical angle be $α$ .
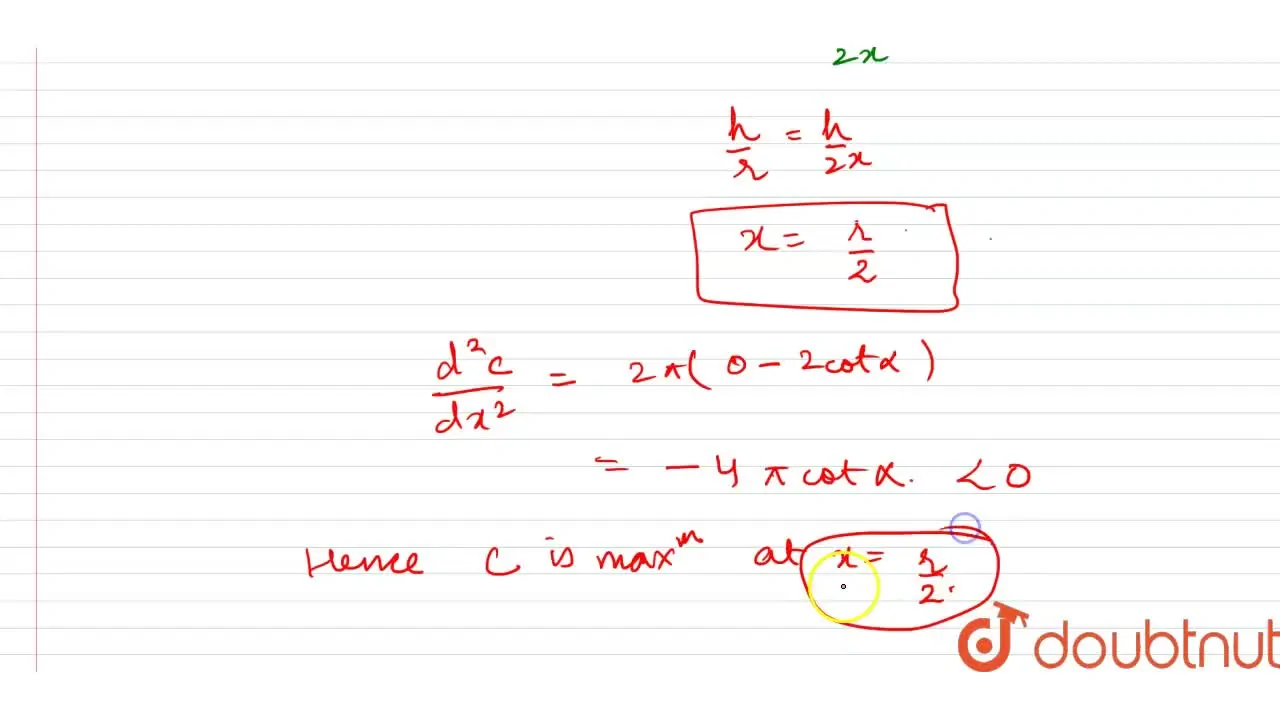
Let the radius of cylinder = $x .' < b r > H e i g h t o f c y l \in d e r = O O' < b r > = A O - A O' < b r > =$ h - x cot alpha $< b r >$ :. $C u r v e d s u r f a c e o f c y l \in d e r < b r >$ C = 2 pi x*(h- x cot alpha) $< b r >$ = 2 pi (hx-x^(2) cot alpha) $< b r >$ rArr (dC)/(dx) = 2 pi (h-2x cot alpha) $< b r > < i m g a \leq ocr_image l o a d \in g = lazy s r c = https://d10lpgp6xz60nq.cloudfront.net/physics_images/NTN_MATH_XII_C06_S01_047_S01.png w h = 80% mx-auto s t y \leq = background:white; > < b r > F or max i m \frac{a}{min} i m a < b r >$ (dC)/(dx) = 0 $< b r >$ rArr h-2x cot alpha = 0 $< b r >$ rArr cot alpha = h/(2x) $< b r >$ rArr h/r = h/(2x) $< b r > (W h e r e' r' = r a d i u s o f t h e c o \neq) < b r >$ rArr x=r/2 $< b r > and$ (d^(2)C)/(dx^(2)) = 2 pi (0-2 cot alpha ) =-4 pi cot alpha lt 0 $< b r >$ rArr $T h e v a l u e o f C i s max i μ m . < b r > H e n c e, t h e c u r v e d s u r f a c e a r e a o f t h e c y l \in d e r w i l l b e max i μ m w h e n$ x= r//2 i.e., the radius of cylinder will be half of the radius of cone.

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A solid metallic right cone is melted and some solid right circular cylinders are made. If the radius of base of each cylinder is half the radius of cone and the height of each cylinder is one third the height of the cone, then the number of cylinders formed are.
A $3$
B $4$
C $5$
D $6$
Question 2 - Select One
The volume and curved surface area of a right circular cylinder are
A $2 π r h, π r^{2} h$
B $π r^{2} h, 2 π r h$
C $\frac{1}{3} π r^{2} h, 2 π r h$
D $π r^{2} h π r h$
Question 3 - Select One
A right circular cylinder and a right circular cone have the same radius and the same volume. The ratio of the height of the cylinder to that of the cone is
A0.12847222222222
B0.086805555555556
C0.12569444444444
D0.04375

NAGEEN PRAKASHAN-APPLICATIONS OF DERIVATIVES-Miscellaneous Exercise

Home
Ask Doubt
Profile