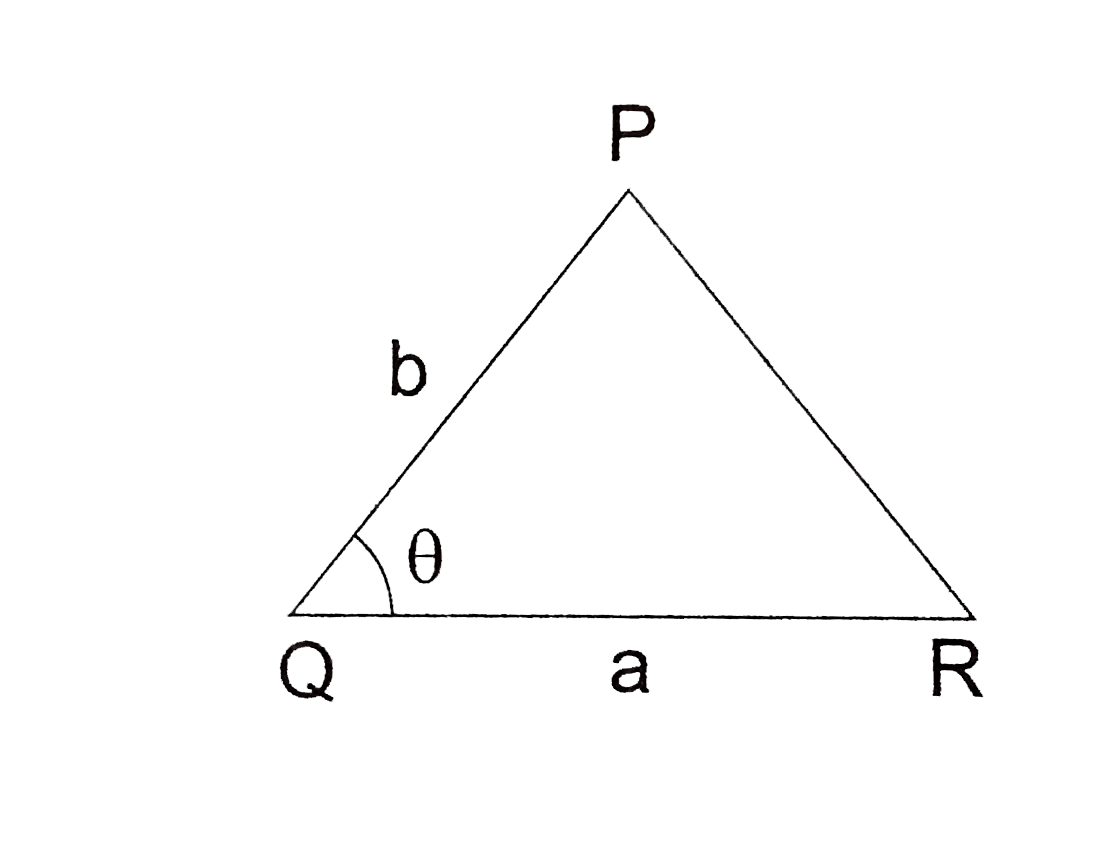
Two sides of a triangle have lengths $' a'$ and $' b'$ and the angle between them is $θ$ . What value of $θ$ will maximize the area of the triangle? Find the maximum area of the triangle also.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{π}{2}$

Let A be the area of $t r a \in g \leq P Q R$
Then, $A = \frac{1}{2} a b sin θ$
$\Rightarrow \frac{d A}{d θ} = \frac{1}{2} a b cos θ$
$\Rightarrow \frac{d^{2} A}{d θ^{2}} = - \frac{1}{2} a b sin θ < 0$
For maxima or minima, we have
$\frac{d A}{d θ} = 0 \Leftrightarrow \frac{1}{2} a b cos θ = 0 \Leftrightarrow cos θ = 0 \Leftrightarrow θ = \frac{π}{2}$
$∴$ A is maximum, when $θ = \frac{π}{2}$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If two sides of a triangle are each k, then its maximum area is
A $k^{2}$
B $\frac{k^{2}}{2}$
C $2 k^{2}$
D $\frac{\sqrt{3} k^{2}}{4}$
Question 2 - Select One
If PQ and PR the two sides of a triangle, then the angle between them which gives maximum area of the triangle is
A $\frac{π}{2}$
B $\frac{π}{3}$
C $\frac{π}{4}$
D $π$

RS AGGARWAL-APPLICATIONS OF DERIVATIVES-Exercise 11F

Home
Ask Doubt
Profile